Математическое моделирование процессов сепарации газов от дисперсной фазы в канале с ленточным завихрителем
Авторы: Лаптев Анатолий Григорьевич, Исхаков Альберт Рифкатович
Рубрика: 13. Химическая технология и промышленность
Опубликовано в
VI международная научная конференция «Технические науки в России и за рубежом» (Москва, ноябрь 2016)
Дата публикации: 27.10.2016
Статья просмотрена: 269 раз
Библиографическое описание:
Лаптев, А. Г. Математическое моделирование процессов сепарации газов от дисперсной фазы в канале с ленточным завихрителем / А. Г. Лаптев, А. Р. Исхаков. — Текст : непосредственный // Технические науки в России и за рубежом : материалы VI Междунар. науч. конф. (г. Москва, ноябрь 2016 г.). — Москва : Буки-Веди, 2016. — С. 56-59. — URL: https://moluch.ru/conf/tech/archive/228/11252/ (дата обращения: 26.04.2025).
В химической, нефтехимической промышленности и энергетике используются различные газообразные среды. Обычно газы имеют неоднородный состав и содержат некоторое количество примесей в виде дисперсной фазы, которую необходимо отделять из-за негативного влияния на технологические процессы и оборудование. Осаждение аэрозолей при этом подходе рассматривается как разновидность диффузионного процесса, что позволяет для его описания использовать уравнения из теории турбулентной миграции частиц и массопередачи. Математическое моделирование является эффективным инструментом при решении задач проектирования или модернизации аппаратов в химической технологии.
При турбулентном течении аэрозоля частицы, будучи невелики по сравнению с масштабом пульсаций газа, вовлекаются в пульсационное движение сплошной среды и совершают вместе с ней интенсивное диффузионное перемещение по потоку. При этом, наличие значительных градиентов осредненной скорости газа и ее пульсационных составляющих в пристеночной области потока вызывает появление еще двух специфических форм движения частиц: продольное скольжение частицотносительно газа со скоростью, соизмеримой со скоростью его течения; поперечная миграция частицсо скоростью, соизмеримой со скоростью турбулентных пульсаций газа.
Эксперименты показали [1], что при турбулентном режиме течения газа скорость осаждения частиц на стенках труб и каналов обычно на несколько порядков превосходит скорость диффузионного (броуновского) осаждения тех же частиц из ламинарного потока и в противоположность последнему возрастает с повышением скорости течения газа, свидетельствуя тем самым об инерционной природе явления. Эта характерная для турбулентных аэродисперсных потоков форма осаждения взвешенных частиц на продольно обтекаемых препятствиях получила название турбулентного осаждения аэрозолей.
Главные силы турбулентного переноса и осаждения аэрозольных частиц — это турбулентная диффузия и турбулентная миграция частиц.
Далее рассмотрен процесс осаждении аэрозоля в вертикальном цилиндрическом канале при турбулентном режиме. По мере движения газожидкостной смеси вдоль канала происходит осаждение частиц на стенках за счет различных механизмов.
Если не учитывать молекулярную диффузию за пределами пограничного слоя, то механизм переноса частиц будет складываться из перемешиваний, обусловленными общими турбулентными вихрями сплошной фазы, общими турбулентными вихрями малых масштабов, обусловленные беспорядочным движением частиц относительно сплошной фазы. Также имеет место продольное перемешивание из-за полной циркуляции в сплошной фазе.
Если аэрозоль имеет концентрацию частиц меньше 2 % об., то преобладающим механизмом является перемешивание за счет общих турбулентных вихрей сплошной фазы.
Обычно при теоретическом анализе всех форм движения дисперсных частиц в турбулентном потоке принимаются следующие предположения [1].
-
Диаметр частиц
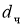 мал по сравнению с масштабом несущих их пульсационных вихрей с масштабом
мал по сравнению с масштабом несущих их пульсационных вихрей с масштабом 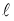 :
: 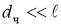 .
.
-
Обтекания частиц происходит при
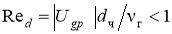 , где
, где 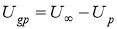 — скорость обтекания частиц турбулентными пульсациями,
— скорость обтекания частиц турбулентными пульсациями,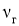 — коэффициент кинематической вязкости газа, м2/с.
— коэффициент кинематической вязкости газа, м2/с.
-
Среднее расстояние между частицами определяется по следующей формуле:
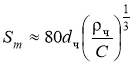 , где
, где 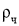 — плотность частиц, кг/м3;
— плотность частиц, кг/м3; 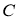 — концентрация, кг/м3.
— концентрация, кг/м3.
Также частицы: не соударяются и не коагулируют друг с другом; не стесняют движение друг друга в ходе взаимных перемещений; не оказывают ощутимого влияния на турбулентные характеристики среды.
Согласно экспериментальным данным Россетти и Пфефера пределом концентраций частиц при выполнении данных условий можно считать ![]() г/м3.
г/м3.
- Частицы имеют близкую к сферической форму. При сильном отклонении от сферы вводится коэффициент формы. Полидисперсность дисперсных частиц рассматривается пофракционно.
- Вторичный срыв и унос частиц со стенки незначителен.
Согласно подходу [1] хаотичное движение частиц в турбулентном потоке газа можно представить как диффузионное движение аэрозольной жидкости, частицы которой имеют меньшую подвижность в
![]() (1)
(1)
и уравнение конвективного массопереноса частиц для плоского канала
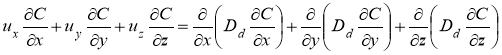 (2)
(2)
с заменой коэффициента турбулентного обмена в газовой фазе Dd на коэффициент турбулентной диффузии частиц Dт [1]: ![]() ,где
,где ![]() ,
,![]() ,
,![]() — скорости движения сплошной фазы вдоль координат
— скорости движения сплошной фазы вдоль координат ![]() ,
, ![]() и
и ![]() соответственно.
соответственно.
Для определения коэффициента турбулентной диффузии используются различные модели.
В двумерном виде уравнение (2) примет следующий вид:
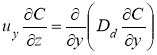 .(3)
.(3)
За пределами пристенного слоя, т. е. в ядре потока примем коэффициент ![]() (y > ), а
(y > ), а ![]() . Задание граничных условий для двухфазного потока на стенке к уравнению (3) является затруднительным, поэтому в данном случае используем подход, когда влияние переноса дисперсной фазы к поверхности стенки (или межфазной поверхности) в уравнении переноса учитывается в виде объемного источника массы.
. Задание граничных условий для двухфазного потока на стенке к уравнению (3) является затруднительным, поэтому в данном случае используем подход, когда влияние переноса дисперсной фазы к поверхности стенки (или межфазной поверхности) в уравнении переноса учитывается в виде объемного источника массы.
Структура двухфазных потоков определяется размерами и распределением элементов дисперсной фазы в сплошной, имеющими общую границу раздела. Для описания таких систем применяются модели гомогенного течения, раздельного течения фаз, потока дрейфа и др. Движение аэрозолей характеризуется практически однородным распределением дисперсной фазы, поэтому далее использован известный подход, когда перенос дисперсной фазы к стенке (или межфазной поверхности) учитывается в виде объемного источника массы.
В общем виде источник массы записывается в следующей форме
Где ![]() — количество массы частиц перешедших из одной фазы в другую, кг/с;
— количество массы частиц перешедших из одной фазы в другую, кг/с; ![]() — объем, м3;
— объем, м3; ![]() — поверхность контакта, м2
— поверхность контакта, м2
Локальный поток массы (1) можно записать в форме аналога уравнения массоотдачи [1]: ![]() , где
, где ![]() — коэффициент скорости переноса частиц турбулентной миграцией, м/с;
— коэффициент скорости переноса частиц турбулентной миграцией, м/с;
Скорость турбулентного осаждения частиц является мерой интенсивности осаждения частиц из турбулентного потока газа на стенках. Под ней подразумевается количество частиц (весовое или численное), осаждающихся из аэрозольного потока на 1 м2 поверхности стенок за 1 с, отнесенное к единичной (по весу или числу) концентрации частиц [1].
С учетом вышеизложенного подхода уравнение (3) получит вид
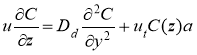 ,(5)
,(5)
где ![]() — поперечная координата к стенке канала, м;
— поперечная координата к стенке канала, м; ![]() — находится используя логарифмический профиль скорости; a — удельная поверхность, м2/м3.
— находится используя логарифмический профиль скорости; a — удельная поверхность, м2/м3.
Граничные условия к уравнению (5): ![]() ,
, ![]() ;
; ![]() ,
, ![]() ;
; ![]() ,
, ![]() , где
, где ![]() — начальная концентрация;
— начальная концентрация; ![]() — высота канала, м.
— высота канала, м.
Данное уравнение справедливо для стационарного процесса и не учитывает входной участок гидродинамической стабилизации.
Повысить эффективность работы трубчатых контактных устройств можно используя закрутку газового потока. При закрученном движении потока происходит увеличение турбулизации потока, повышается перепад давления и эффективность процессов переноса.
Закрутку потока в цилиндрическом канале обычно организуют путем установки во внутреннее пространство ленточного завихрителя.
Для учета ленточного завихрителя запишем уравнение (5) в проекции на вертикальную ось:
![]() ,(6)
,(6)
где ![]() — средняя скорость газа в слое, м/с;
— средняя скорость газа в слое, м/с; ![]() — угол подъема винтовой линии (закрутки потока).
— угол подъема винтовой линии (закрутки потока).
Граничные условия: при ![]() ,
, ![]() ; при
; при ![]() ,
, ![]() .
.
При ![]() уравнение (6) упрощается:
уравнение (6) упрощается: 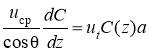
и в конечных разностях запишется следующим образом:
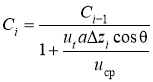 .(7)
.(7)
Динамическая скорость газовой смеси ![]() определяется по следующей зависимости, полученной из уравнения баланса сил:
определяется по следующей зависимости, полученной из уравнения баланса сил:
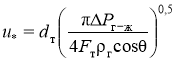 ,(8)
,(8)
где ![]() — перепад давления, обусловленный трением газа и жидкости, Па;
— перепад давления, обусловленный трением газа и жидкости, Па; ![]() — поверхность трубки, м2.
— поверхность трубки, м2.
Угол подъема винтовой линии: 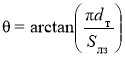 , где
, где ![]() — шаг витка ленты, м.
— шаг витка ленты, м.
Перепад давления
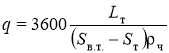 .
.
При q > 1 м3 / м ч перепад давления находится экспериментально, а при q < 1 м3/м·ч считается, что трубки практически не орошаются:
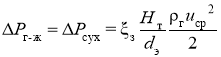 ,(9)
,(9)
где з — коэффициент гидравлического сопротивления, вызванный закруткой, ![]() — перепад давления для сухого канала, Па.
— перепад давления для сухого канала, Па. 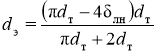 , где
, где![]() — толщина ленты, м.
— толщина ленты, м.
В зависимости от критического значения числа Рейнольдса 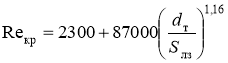 ,расчет коэффициентов сопротивления можно выполнить по уравнениям Щукина при
,расчет коэффициентов сопротивления можно выполнить по уравнениям Щукина при ![]() :
:
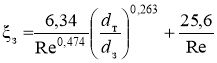 .
.
При турбулентном режиме ![]() :
:
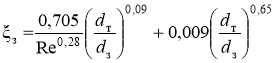 ,где
,где 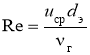 , dз — диаметр кривизны спирального канала, м.
, dз — диаметр кривизны спирального канала, м.
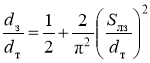 .
.
Зависимость для ξз справедлива при 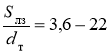 .
.
Таким образом, на основе применения уравнения конвективного массопереноса частиц получены выражения для определения профиля изменения концентрации по высоте цилиндрического канала с ленточным завихрителем. Представленные модели могут быть использованы проектными организациями при разработке аппаратов газоочистки.
Литература:
- Медников Е. П. Турбулентный перенос и осаждение аэрозолей. — М.: Наука, 1980. — 176 с.











