Решение задач строительной механики по определению максимального прогиба и основной частоты колебаний треугольных пластинок с помощью МИКФ
Автор: Фетисова Мария Александровна
Рубрика: 8. Строительство
Опубликовано в
V международная научная конференция «Современные тенденции технических наук» (Казань, май 2017)
Дата публикации: 10.04.2017
Статья просмотрена: 85 раз
Библиографическое описание:
Фетисова, М. А. Решение задач строительной механики по определению максимального прогиба и основной частоты колебаний треугольных пластинок с помощью МИКФ / М. А. Фетисова. — Текст : непосредственный // Современные тенденции технических наук : материалы V Междунар. науч. конф. (г. Казань, май 2017 г.). — Казань : Бук, 2017. — С. 40-46. — URL: https://moluch.ru/conf/tech/archive/230/12248/ (дата обращения: 18.04.2025).
Для пластинок в виде равнобедренных с комбинированными граничными условиями (комбинация жесткого защемления и шарнирного опирания) построены аппроксимирующие функции по решениям, полученным с помощью МКЭ для задач поперечного изгиба пластинок равномерно распределенной нагрузкой и свободных колебаний в ненагруженном состоянии. Доказано, что эти аппроксимирующие функции ограничивают область распределения всего множества значений максимального прогиба и основной частоты колебаний треугольных пластинок произвольного вида, представленную в координатных осях «физическая характеристика — угол при основании треугольника». Показано, что с помощью метода интерполяции по коэффициенту формы (МИКФ) можно с использованием найденных граничных кривых достаточно просто получить решение для пластинки в виде произвольного треугольника с комбинированными граничными условиями.
Ключевые слова: аффинное преобразование, интерполяция, коэффициент формы, комбинированные граничные условия, треугольник, пластинка
Теоретические основы МИКФ разработаны А. В. Коробко [1]. Сущность метода заключается в установленной автором функциональной взаимосвязи между интегральными физическими характеристиками пластинок F и коэффициентом их формы Kf, который для треугольных пластинок определяется по формуле
![]() (1)
(1)
где α, β и γ — углы треугольника.
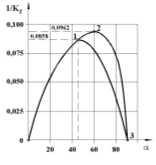
Рис. 1
Изучая изопериметрические свойства коэффициента формы и интегральных физических характеристик треугольных пластинок, было доказано, что при геометрических преобразованиях треугольной области эти два параметра изменяются подобным образом. Для иллюстрации этого утверждения рассмотрим рисунки 1 и 2. На рисунке 1 приводится график изменения величины 1/Кf для равнобедренных и прямоугольных треугольников в зависимости от правого угла при основании; на рисунке 2 — график изменения величины 1/ω (ω — основная частота колебаний) для треугольных пластинок с шарнирным опиранием сторон (схема а)) и жестким защемлением по контуру (схема б)). На этих рисунках точка 2 соответствует правильному треугольнику, точка 1 — равнобедренному прямоугольному треугольнику; кривая 0–1 соответствует пластинкам в виде равнобедренных тупоугольных треугольников, кривая 1–2–3 — в виде равнобедренных остроугольных треугольников, кривая 1–3 — в виде прямоугольных треугольников.
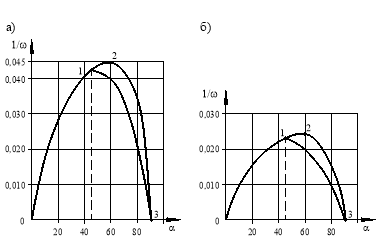
Рис. 2
Сопоставляя изображенные на этих рисунках кривые, нетрудно заметить аналогию в распределении основной частоты колебаний и коэффициента формы. Поэтому, все изопериметрические свойства коэффициента формы, которые подробно исследованы в работе [1], можно автоматически перенести на основную частоту колебаний.
На основании изопериметрических свойств коэффициента формы в работе [1] сформулированы изопериметрические теоремы для треугольных пластинок:
‒все множество интегральных физических характеристик для треугольных областей ограничено кривой 0–1–2–3, соответствующей равнобедренным треугольникам;
‒все множество интегральных физических характеристик для областей в виде остроугольных треугольников ограничено кривыми, соответствующими равнобедренным треугольникам (кривая 1–2–3) и прямоугольным треугольникам (кривая 1–3);
‒все множество интегральных физических характеристик для областей в виде тупоугольных треугольников ограничено кривыми, соответствующими равнобедренным треугольникам (кривая 1–2) и прямоугольным треугольникам (кривая 1–3).
Если для какой-либо задачи технической теории пластинок построены рассмотренные выше граничные кривые, то с помощью МИКФ можно получить решение для любой треугольной пластинки. При этом необходимо выполнить следующую последовательность действий:
‒ выбрать геометрическое преобразование (обычно аффинный сдвиг с растяжением), при котором из заданной области можно получить два равнобедренных треугольника (опорные фигуры);
‒ по соответствующим аппроксимирующим (граничным) кривым найти значение интегральных физических характеристик для опорных фигур (опорные решения);
‒ подобрать функцию вида F = KQ(Kf)n, где Q обобщенная физико-геометрическая константа для конкретной рассматриваемой задач теории пластинок;
‒ по опорным решениям найти неопределенные параметры К и n;
‒ подсчитать коэффициент формы для заданной фигуры и, подставив его в аппроксимирующую функции. F(Kf), найти значение F для нее.
Граничные аппроксимирующие кривые были построены для пластинок в виде равнобедренных треугольников с условиями на контуре, изображенными на рисунке 3. Для их построения с помощью МКЭ с использованием современных программных комплексов были получены решения для множества треугольных пластинок с углом при основании, изменяющимся от 15о до 80о[1] с интервалом в 5...10о. Найденные решения для задач поперечного изгиба и свободных колебаний пластинок приведены в таблице 1.
Таблица 1
Значения максимального прогиба иосновной частоты колебаний для пластинок в виде равнобедренного треугольника скомбинированными граничными условиями
|
№ п/п |
Угол при основании треугольника, αо |
||||||||||
|
15 |
20 |
30 |
40 |
45 |
50 |
55 |
60 |
65 |
70 |
80 |
|
|
Поперечный изгиб пластинок (w0 = KqA2/D) |
|||||||||||
|
1 |
0,524 |
0,919 |
1,571 |
2,293 |
2,607 |
2,812 |
3,008 |
3,086 |
2,986 |
2,688 |
1,610 |
|
2 |
0,228 |
0,412 |
0,798 |
1,222 |
1,447 |
1,654 |
1,826 |
1,949 |
2,000 |
1,952 |
1,303 |
|
3 |
0,234 |
0,362 |
0,737 |
1,044 |
1,172 |
1,263 |
1,303 |
1,283 |
1,201 |
1,047 |
0,508 |
|
4 |
0,0858 |
0,194 |
0,388 |
0,604 |
0,715 |
0,782 |
0,850 |
0,872 |
0,847 |
0,777 |
0,425 |
|
Свободные колебания пластинок |
|||||||||||
|
1 |
52,456 |
41,610 |
31,121 |
26,156 |
24,615 |
23,454 |
22,887 |
22,639 |
22.900 |
23,841 |
31,058 |
|
2 |
82,075 |
62,566 |
44,273 |
35,850 |
33,089 |
30,993 |
29,519 |
28,529 |
28,175 |
28,516 |
34,642 |
|
3 |
81,549 |
63,392 |
46,253 |
39,003 |
36.826 |
35,584 |
35,110 |
35,270 |
36,504 |
39,064 |
55,50 |
|
4 |
114,53 |
91,226 |
62,929 |
51,227 |
47,466 |
45,064 |
43,620 |
42,925 |
43,514 |
45,409 |
60,797 |
|
Примечание: 1. В приведенных в таблице формулах использованы следующие обозначения: А — площадь, D — цилиндрическая жесткость, m — масса единицы площади пластинки. 2. Величина прогиба увеличена в 103 раз. 3. Жирным шрифтом выделены экстремальные значения w0 и ω, а курсивом — неочевидные результаты. |
|||||||||||
Анализ приведенных данных показывает:
1) для треугольных пластинок с однородными граничными условиями максимальный прогиб соответствует равностороннему треугольнику (α = 60о);
2) для треугольных пластинок с комбинированными граничными условиями положение экстремума смещается: для схемы опирания, представленной на рисунке 3-б, смещение происходит вправо и экстремум соответствует равнобедренному треугольнику с углом при основании ≈65о (угол при вершине ≈50о); для схемы опирания, представленной на рисунке 3-в, смещение происходит влево и экстремум соответствует равнобедренному треугольнику с углом при основании ≈55о (угол при вершине ≈70о);
3) при переходе последовательно от схемы опирания пластинки а) к схеме г) (рис. 3) значения максимального прогиба уменьшаются, за исключением пластинок с углом при основании равнобедренного треугольника α = 15о (в таблице эти результаты выделены курсивом).
Точно такие же эффекты проявляются и для основной частоты колебаний.
|
а) |
б) |
|
|
|
|
в) |
г) |
|
|
|
|
Рис. 3 |
|
|
а) |
б) |
|
|
|
|
Рис. 4 |
|
Причиной возникновения подобного рода эффектов является влияние жестко защемленного края (см. рис. 4, где жирными линиями внутри треугольника показаны положения нейтральных линий — линий, вдоль которых изгибающие моменты Мn равны нулю):
‒ при однородных граничных условиях влияние границ одинаковое, поэтому экстремумы w0 и ω достигаются для пластинок в виде равностороннего треугольника;
‒ при появлении жестко защемленных сторон в треугольной пластиннике нейтральными линиями (см. рис. 4) ограничивается уже не равносторонний треугольник, а более сложная фигура, у которой стороны, параллельные защемленному краю треугольной пластинки в средней части, отклоняются, поворачивая в углы пластинки;
‒ неочевидное, на первый взгляд, увеличение максимального прогиба и уменьшение основной частоты колебаний для пластинки, опертой по схеме 3-в, по сравнению со схемой 3-б можно объяснить тем, что для пластинок с очень острыми углами при вершине при сближении нейтральной линии и угла пластинки у схемы 3-б влияние жесткости угла оказывается большим, чем влияние жестко защемленного края у схемы 3-в.
Граничные аппроксимирующие функции строились по значениям w0 и ω, приведенным в таблице 1, с помощью программного комплекса Table curve. При этом преследовалась цель, построить эти функции как можно с большей точностью, поскольку они в дальнейшем лягут в основу создания подпрограммы «МИКФ-треугольники» для общего программного комплекса «МИКФ». Этим и объясняется высокая степень полинома, с помощью которого подбирались аппроксимирующие функции. Такие функции были построены для всех случаев опирания треугольных пластинок для обеих рассматриваемых задач. Например:
‒ для шарнирно опертых по контуру пластинок:
![]() (2)
(2)
где а = 58,945, b = –16,451, c = 1,964, d = –0,132, e = 0,00556, f = –0,000154, g = 2,856∙10–6,
h = –3,510∙10–8, i = 2,744∙10–10, j = –1,237∙10–12, k = 2,444∙10–15;
![]() (3)
(3)
где а = 38,896, b = –57,185, c = 36,980, d = –13,811, e = 3,285, f = –0,516, g = 0,0536,
h = –0,00356, i = 0,000136, j = –2,311∙10–6;
‒ для пластинок, боковые стороны которых шарнирно оперты, а основание жестко защемлено:
![]() (4)
(4)
где а = –16,358, b = 4,370, c = –0,504, d = 0,0333, e = –0,00140, f = 3,867∙10–5, g = –7,199∙10–7, h = 8,906∙10–9, i = –7,019∙10–11, j = 3,189∙10–13, k = –6,356∙10–16;
![]() (5)
(5)
где а = –0,0277, b = 0,00859, c = –0,000939, d = 6,445∙10–5, e = –2,775∙10–6, f = 7,791∙10–8, g = –1,450∙10–9, h = 1,777∙10–11, i = –1,380∙10–13, j = 6,170∙10–16, k = –1,214∙10–18.
Метод интерполяции по коэффициенту формы имеет несколько возможностей, которые сводятся к решению следующих задач:
‒ качественная оценка области распределения интегральных физических характеристик определенного (заданного) подмножества форм пластинок;
‒ двусторонняя оценка физической характеристики пластинки конкретного вида путем построения двусторонних изопериметрических неравенств;
‒ построение аналитической зависимости, характеризующей изменение интегральной физической величины для некоторого подмножества областей, объединенных одним непрерывным или дискретным геометрическим преобразованием, и определение с ее помощью физической характеристики для пластинки определенного вида из заданного подмножества форм.
Методика реализация первой задачи сводится к изучению изопериметрических свойств и закономерностей распределения коэффициента формы для областей определенного вида. Получив качественную картину распределения коэффициента формы для заданного класса областей (рис. 1), можно сразу же получить и приближенную количественную оценку распределения интегральных физических характеристик, если известно хотя бы одно решение для пластинки определенного вида из этого класса областей. Количественная оценка получается линейным масштабированием графика Kf — α путем приравнивания ординат графиков Kf — α и F — α для пластинки с известным решением.
Покажем эту возможность на примере задачи об основной частоте колебаний треугольных пластинок с шарнирно опертым контуром [1]. Пусть нам известно единственное решение для пластинки в виде равностороннего треугольника (α = 60о, Kf = 10,392 [1], ω = = ![]() ). Разделим Kf на коэффициент пропорциональности при ω (Kf/ω = = 10,392/22,792 = 0,456) и умножим график 1\Kf — α на 0,456
). Разделим Kf на коэффициент пропорциональности при ω (Kf/ω = = 10,392/22,792 = 0,456) и умножим график 1\Kf — α на 0,456![]() При этом получится новый график, у которого ордината вершины соответствует величине 1/ω для равностороннего треугольника, а весь график является подобным графику, изображенному на рисунке 2-а. К сожалению, указанное подобие нелинейное и полученный новый график не является точным изображением графика 1/ω — α. Однако он дает достаточно хорошее приближение к действительному графику. Например, для шарнирно опертой пластинки в виде равнобедренного прямоугольного треугольника (α = 45о, Кf = 11,657) из построенного графика будем иметь:
При этом получится новый график, у которого ордината вершины соответствует величине 1/ω для равностороннего треугольника, а весь график является подобным графику, изображенному на рисунке 2-а. К сожалению, указанное подобие нелинейное и полученный новый график не является точным изображением графика 1/ω — α. Однако он дает достаточно хорошее приближение к действительному графику. Например, для шарнирно опертой пластинки в виде равнобедренного прямоугольного треугольника (α = 45о, Кf = 11,657) из построенного графика будем иметь:
что отличается от известного точного решения ![]() на 3,60 %.
на 3,60 %.
Для построения двусторонних изопериметрических неравенств при оценке интегральных физических характеристик пластинок необходимо знание границ возможного распределения этих характеристик для некоторого подмножества форм пластинок.
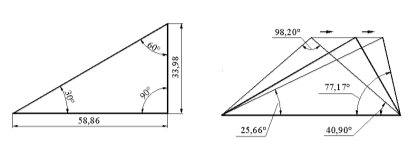
Построение двусторонних изопериметрических неравенств можно проиллюстрировать с помощью рисунка 5, на котором показан пример аффинного сдвига равнобедренного тупоугольного треугольника с углом при вершине 98,20о (Кf = 12,460) параллельно основанию. При этом из него получаются прямоугольный треугольник с углами 30о и 60о (Кf = 12,928) и равнобедренный остроугольный треугольник с углом при вершине 25,66о (Кf = 13,795).
Известно [2], что при аффинном сдвиге коэффициент формы получаемых фигур монотонно увеличивается. Это означает, что частота колебаний будет также монотонно увеличиваться.
|
а) |
б) |
|
|
|
|
Рис. 5 |
|
Таким образом, значения основных частот колебаний пластинок в виде указанных равнобедренных треугольников будут давать верхнюю и нижнюю оценки частоты колебаний для пластинки в виде прямоугольного треугольника. По формуле (3) для этих равнобедренных треугольных пластинок будем иметь:
![]() ,
, ![]() .
.
Согласно основной изопериметрической теореме по этим данным можно построить двусторонние изопериметрические неравенства
![]() ≤ ω ≤
≤ ω ≤ ![]()
которые удовлетворяются для всех треугольных пластинок, объединенных указанным преобразованием. Известное точное решение задачи об основной частоте заданной пластинки в виде прямоугольного треугольника ( = 26,58![]() ) действительно лежит внутри указанных границ.
) действительно лежит внутри указанных границ.
Для более точного определения основной частоты колебаний заданной треугольной пластинки следует по опорным решениям построить аналитическую зависимость вида F = KQ(Kf)n, соответствующую выбранному преобразованию. Используя методику МИКФ, получим: ![]()
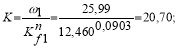
= 20,7(Кf)0,0903
Подставляя в эту формулу значение коэффициента формы для заданной пластинки в виде прямоугольного треугольника (Kf = 12,928), найдем:
= 26,08![]() ,
,
что на 1,89 % отличается от известного точного аналитического решения.
Таким образом, полученные в данной статье решения для задач поперечного изгиба и свободных колебаний пластинок в виде равнобедренных треугольников с однородными и комбинированными условиями опирания на контуре, позволяют построить граничные аппроксимирующие функции и с их помощью, используя методику МИКФ, рассчитывать пластинки для любого вида треугольных пластинок с любой комбинацией граничных условий вдоль их сторон.
Литература:
- Коробко А. В. Геометрическое моделирование формы области в двумерных задачах теории упругости. — М.: Изд-во АСВ, 1999. — 304 с.
- Коробко В. И. Изопериметрический метод в строительной механике: Теоретические основы изопериметрического метода. — М.: Изд-во АСВ, 1997. — 390 с.
- Коробко А. В., Фетисова М. А. Определение поперечного изгиба методом интерполяции по коэффициенту формы при аффинном преобразовании пластинок в виде ромбов и параллелограммов Промышленное и гражданское строительство. 2010. № 1. С. 23–24.
- Фетисова М. А. Развитие и применение метода интерполяции по коэффициенту формы к решению задач поперечного изгиба пластинок с комбинированными граничными условиями. Диссертация на соискание ученой степени кандидата технических наук / Орловский государственный технический университет. Орел, 2010
- Фетисова М. А., Володин С. С. Применение метода интерполяции по коэффициенту формы для решения задач строительной механики. Молодой ученый. 2013. № 3. С. 114–116.
- Фетисова М. А., Володин С. С. Коэффициент формы как геометрическая характеристика. Молодой ученый. 2011. Т. 1. № 5. С. 105.
- Коробко А. В., Фетисова М. А. Способы решения задач поперечного изгиба трапециевидных пластинокСтроительство и реконструкция. 2010. № 1. С. 36.
- Фетисова М. А., Калашникова Н. Г. Определение максимального прогиба трапециевидных пластинок с комбинированными граничными условиями с помощью МИКФ. Известия Орловского государственного технического университета. Серия: Строительство и транспорт. 2009. № 1. С. 65.
- Фетисова М. А. Определение максимального прогиба параллелограммных и трапециевидных пластинок с помощью МИКФ Молодой ученый. 2008. № 1. С. 36–40.
- Борисова Н. В. Особенности проектирования и расчета деревянных ферм на металлических зубчатых пластинах. В сборнике: Вестник строительства и архитектуры Сборник научных трудов. Орел, 2014. С. 105–108.
[1] При значениях угла α < 15o и α > 80o решения, получаемые с помощью МКЭ, начинали резко отклоняться от плавно и монотонно изменяющихся значений F внутри интервала 15о < α < 80o.