Определение воздействия внутренних и внешних угроз на информационную систему персональных данных с помощью построения математической модели



Каждая информационная система в той или иной степени имеет свои особенности в работе. Для того что бы дать формализованное описание структуры и процесса функционирования информационной системы необходимо создать математическую модель. Математическая модель позволяет представить процесс функционирования системы в виде, допускающем аналитическое исследование системы с использованием методов, разработанных в рамках данного математического аппарата, что в свою очередь позволяет идентифицировать неисправности, уязвимости и недостатки данной информационной системы. Основными требованиями к построенной модели являются ее достаточность для решения поставленных задач и практическая целесообразность (удобство в использовании).

Цель данной работы — на основе типичной информационной системы по обработке персональных данных построить математическую модель воздействия угроз и разработать методику их выявления.

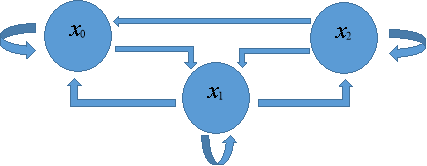
Рис. 1. Состояние системы

Данную информационную систему будем рассматривать как систему массового обслуживания, в которую поступают угрозы. Для начала рассмотрим вариант того что на систему поступают угрозы одного типа, учитывая, что данная угроза не может быть реализована или наступить несколько раз в один и тот же момент времени. Согласно этим условиям мы строим ориентированный граф (рис. 1) который показывает три различных состояния системы: а) начальное состояние (угрозы не было); б) измененное состояние (нереализованная угроза); в) критическое состояние (реализованная угроза).

Для построения математической модели системы об условимся, что у данной системы отсутствуют поглощающие состояния, т. е. реализованная угроза либо никак не влияет на работоспособность системы в целом, либо выводит из строя на непродолжительный срок один из ее сегментов. Это указывает на то, что система из любого состояния имеет возможность вернуться в исходное состояние, что позволяет нам изучить ее поведение в течении длительного промежутка времени.

Переход системы из состояния в состояние показан с помощью ориентированного графа на рис.1. Данная информационная система является системой с восстановлением, т. к. согласно вышеупомянутому она не имеет поглощающие состояния, а это означает, что из состояния Х2 система может вернуться в исходное состояние. Для описания процесса перехода системы построим матрицу интенсивностей перехода 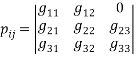[1]:

(1)

Согласно условиям, предъявляемым к матрице интенсивностей перехода [1], все элементы этой матрицы должны удовлетворять условию 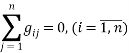, получим:

(2)

В данной работе используется вероятностно-аналитический способ определения элементов матрицы интенсивностей переходов в соответствии с видом информационной системы (рис.1). Для определения вероятностей строим систему дифференциальных уравнений с начальными условиями

(3) которая имеет следующий вид:

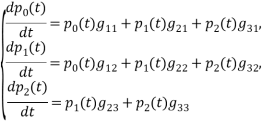(4)

Данную математическую модель (3), (4) рассматриваемой информационной системы, можно численно решить с помощью задачи Коши с использованием специальных математических программ (например, SMath Studio Cloud)

Если переход системы из состояния в состояние осуществляется в строго определенный момент времени t, т. е. является дискретным, то матрица вероятностей перехода из состояния в состояние за один шаг имеет вид (1), иначе матрица за n- шагов (t=n) приобретает следующий вид [3,4]:

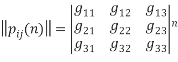(5)

Таким образом данная математическая модель определяет воздействия внутренних и внешних угроз на информационную систему персональных данных.

Литература:

1. Алиев Т. И. Основы моделирования дискретных систем: учебное пособие. — СПб: СПбГУ ИТМО, 2009. — 363 с.

2. Волков И. К., Зуев С. М., Цветкова Г. М. Случайные процессы: учебник для вузов / под ред. В. С. Зарубина, А. П. Крищенко. — М.: МГТУ им.Баумана, 1999. — 448с.

3. Теоретические основы анализа и оценки влияния внутренних угроз на безопасность конфиденциальной информации: монография / А. П. Росенко. — М.: Гелиос АРВ, 2008. — 154 с