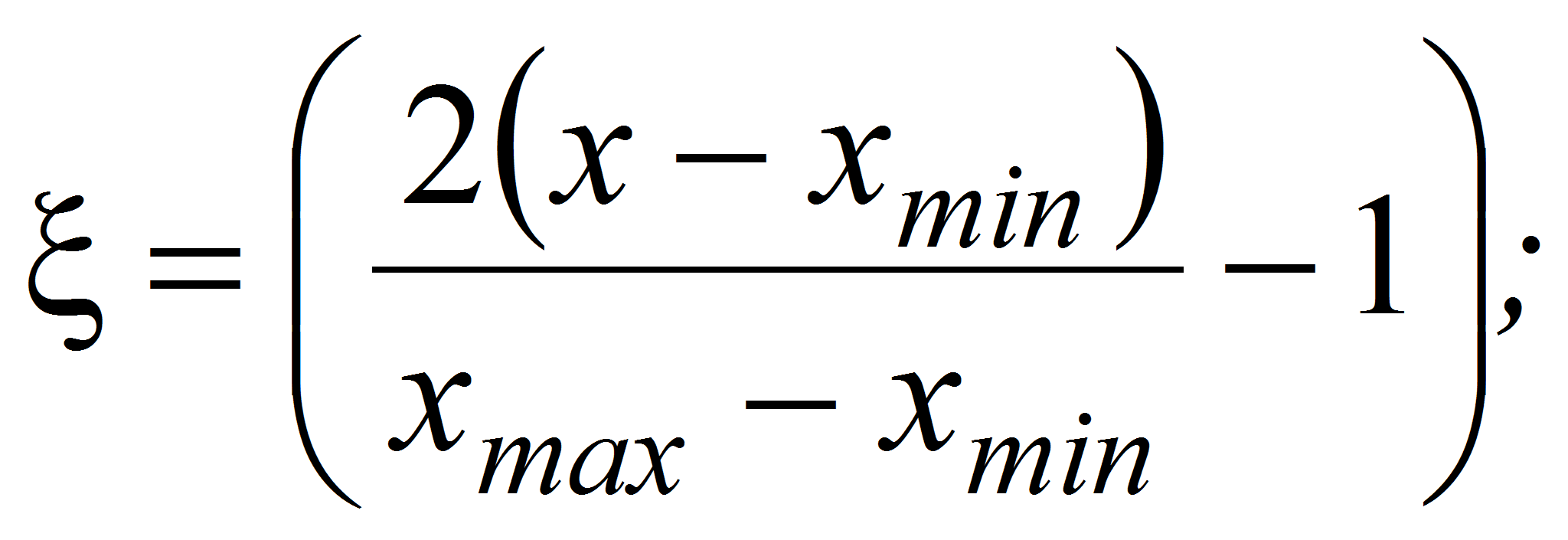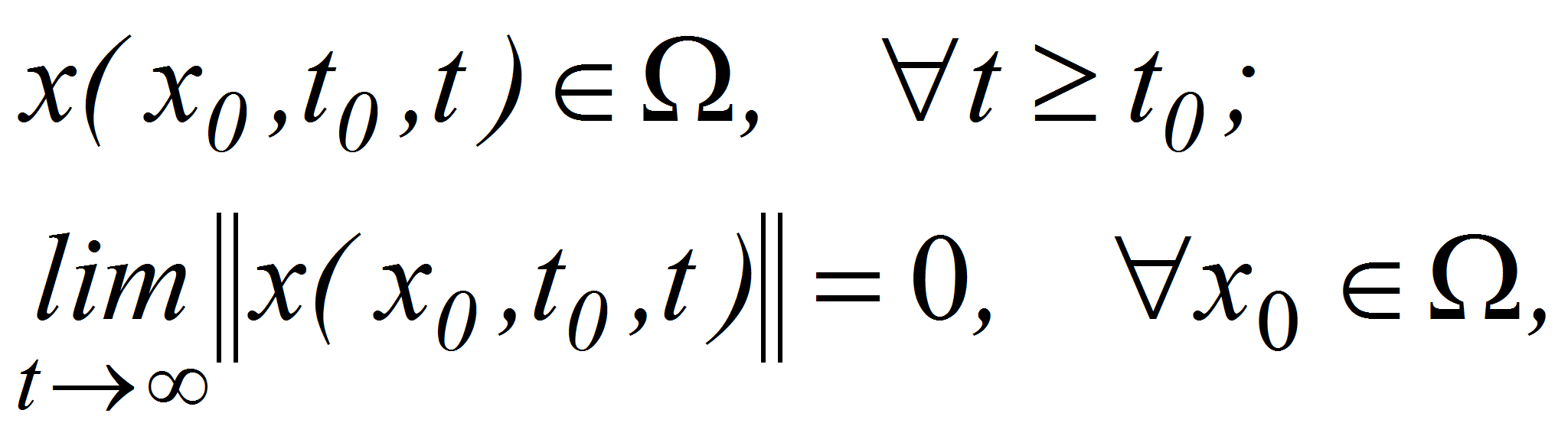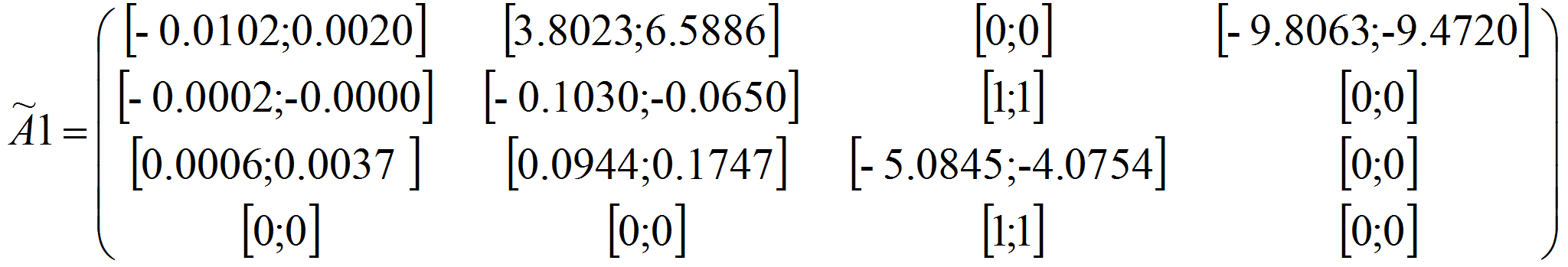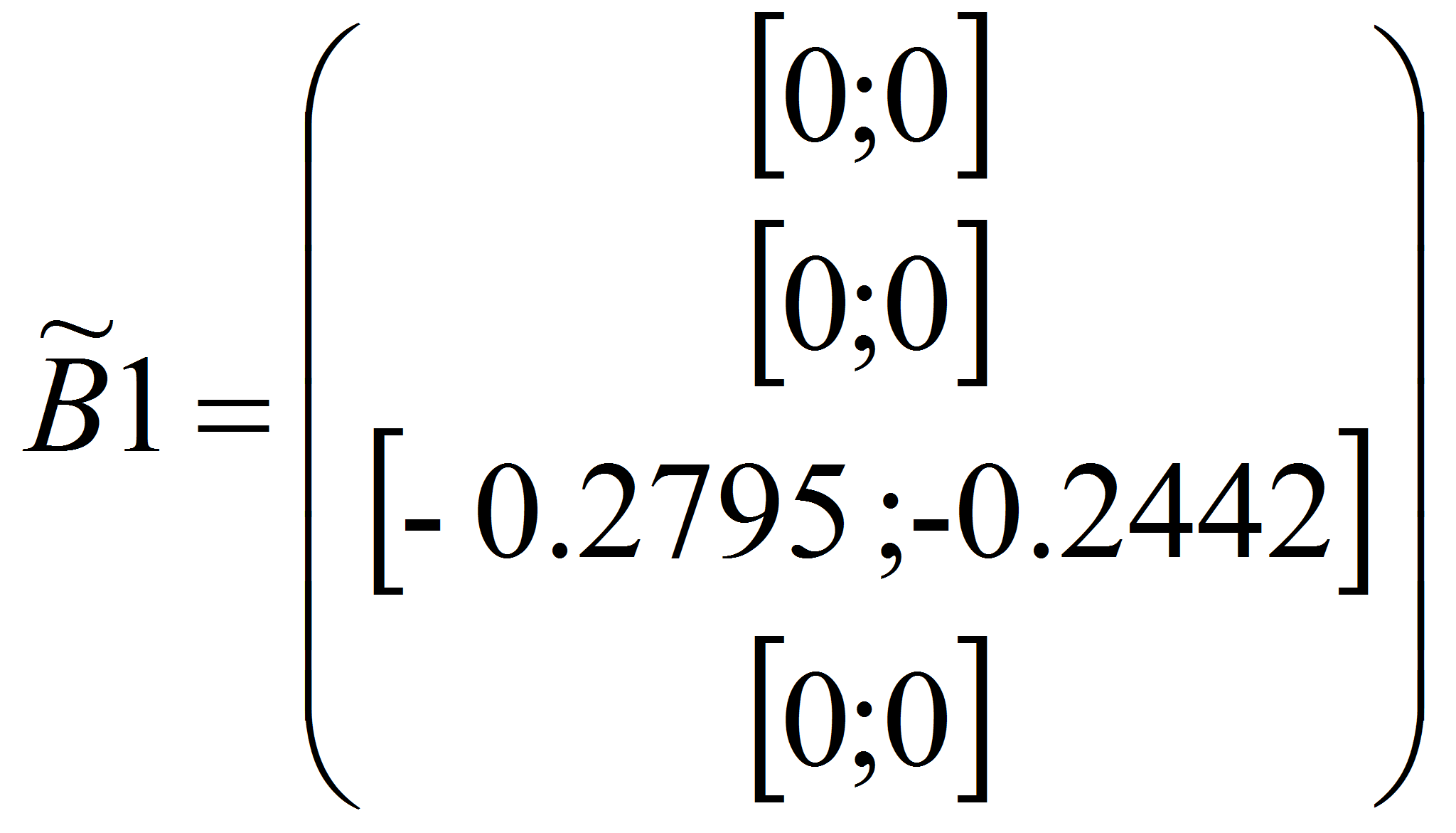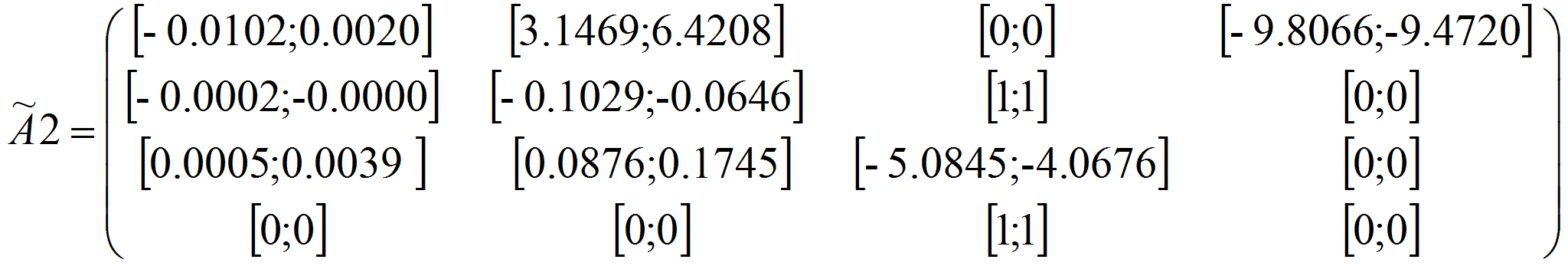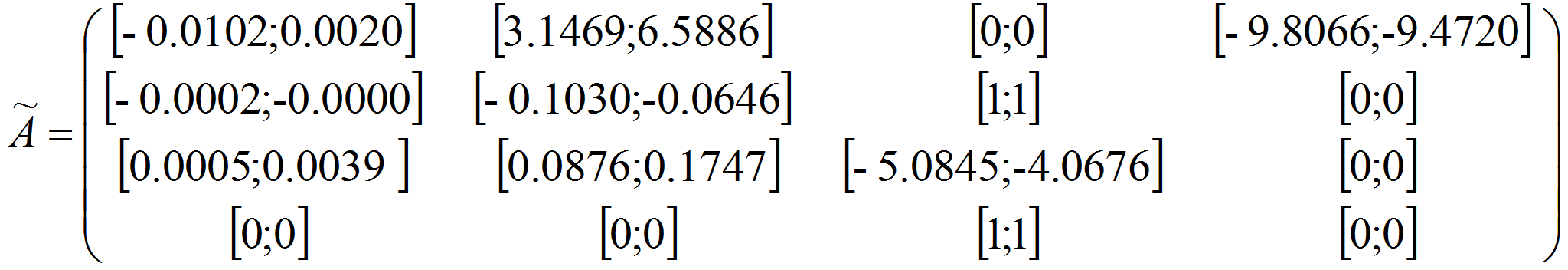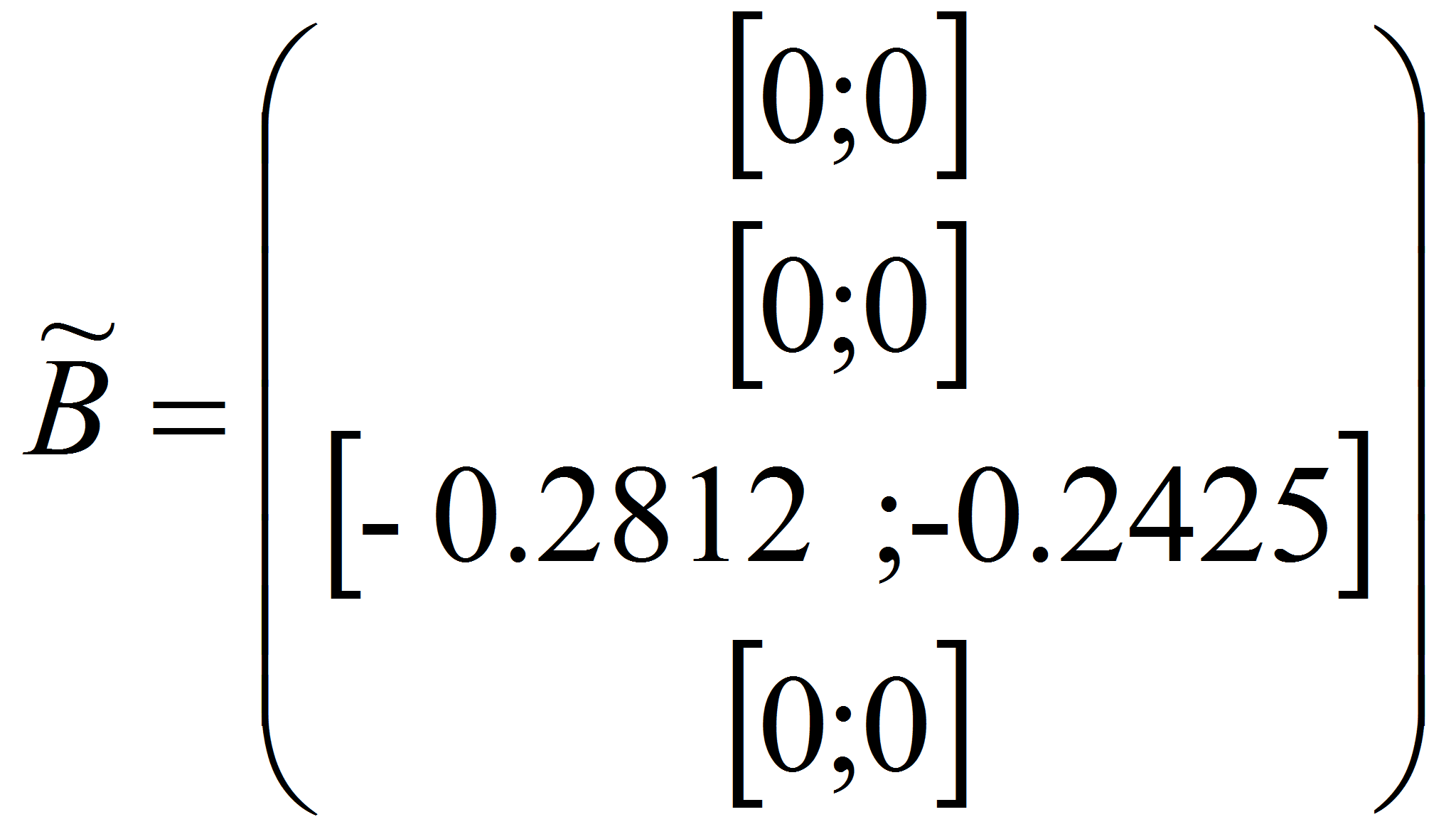Исследование области притяжения нелинейной системы в условиях интервальной неопределенности

При проектировании летательных аппаратов (ЛА) важное значение имеют вопросы исследования устойчивости и определения допустимы значений параметров, характеризующих состояние ЛА, при которых обеспечивается устойчивое состояние. ЛА – сложный объект, описываемый в общем случае нелинейными дифференциальными уравнениями больших порядков. В работе предложена методика расчета интервальной матрицы, необходимой для синтеза автопилота, обеспечивающего заданную область притяжения,

Рассмотрим систему дифференциальных уравнений, описывающих продольное движение ЛА [1].

(1)

где V – скорость самолёта истребителя, m – его масса,, – проекции суммы внешних силы, действующих на ЛА, и тяги на соответственно оси Ox, Oy связанной системы координат, – проекция момента внешних сил на ось Oz, – угловая скорость относительно оси Oz, – угол тангажа, – момент инерции относительно оси Oz.

Для разложения в ряд Тейлора уравнений (1) необходимо знать аналитическое выражение величин , , . Данные зависимости сложны и определяются из теоретических выводов и опытных испытаний [1-3]. Результаты опытных испытаний имеют графическое представление [2], для определения их аналитических зависимостей предлагается применить аппроксимацию полиномами Чебышева [4]:

,

, (2)

,

где – искомая аналитическая зависимость аппроксимированной функции определённой на интервале ;

– полиномы Чебышева,

– дискретные значения функции, полученные из графических зависимостей

– сглаженные дискретные значения функции,

x – область определения искомой функциональной зависимости.

Для численных расчётов, были использованы характеристики на самолёт МИГ 29.

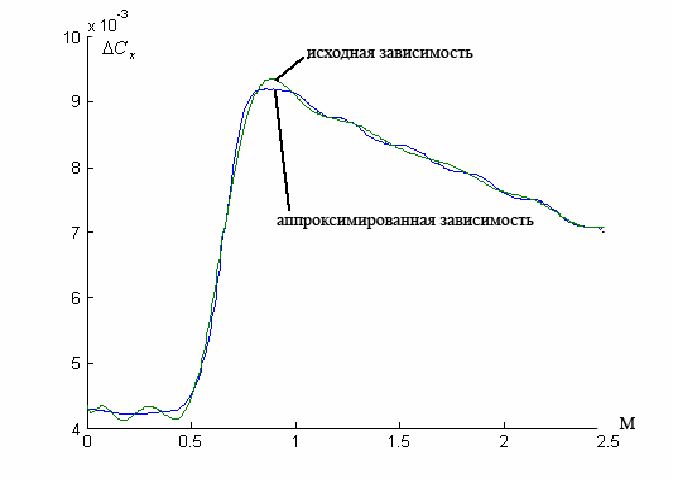
Пример аппроксимации данным методом представлен на рисунке 1, здесь изображена зависимость дополнительного коэффициента лобового сопротивления от числа Маха.

Рис. 1. Аппроксимация зависимости дополнительного коэффициента лобового сопротивления от числа Маха ортогональными полиномами Чебышева

Пусть исследуемая система описывается совокупностью обыкновенных дифференциальных уравнений

_. (3)

Разложив функцию в ряд Тейлора и пренебрегая нелинейной частью этого разложения, получим

, (4)

где .

По линейному приближению (4) можно судить о свойствах системы (3) в малой окрестности точки разложения.

Однако на практике нужно знать, в какой окрестности исходной точки линеаризованная модель сохраняет свою адекватность и при каких отклонениях недопустимо пренебрегать нелинейными слагаемыми. Для этого используется понятие области притяжения положения равновесия нелинейной системы (3).

В общем случае под областью притяжения &#; системы (3) понимают наибольшую область начальных отклонений x(0), при которых решения этой системы являются асимптотически устойчивыми, или, иначе, устойчивые решения, удовлетворяющие условиям

(5)

принадлежат области притяжения нулевого положения равновесия системы (3).

Пусть область притяжения задается в виде многомерного параллелепипеда в пространстве состояний исследуемой системы

. (6)

Чтобы найти соотношения, при выполнении которых система будет устойчивой в области (6), осуществим линеаризацию ее математической модели в вершинах данного параллелепипеда. В результате получим следующий спектр линеаризованных моделей

. (7)

Дальнейшее исследование предполагает построение интервальной матрицы вида

, , (8)

где – множество матриц, элементами которых являются вещественные интервалы ; – интервальные элементы этой матрицы, нижние и верхние границы которых вычисляются следующим образом. В случае, когда функции являются монотонными в области (4) или, что-то же самое, функции являются знакоопределенными в этой области, тогда

где , ; (9)

В противном случае

где . (10)

Задача нахождения минимума или максимума вещественной функции решается двумя методами: метод Хука и Дживса и метод генетического алгоритма.

Генетический алгоритм (ГА) – метод оптимизации, основанный на концепциях естественного отбора и генетики. Генетические алгоритмы максимизируют многопараметрические функции. Генетический алгоритм состоит из следующих шагов:

1. Генерация начальной популяции. Начальная популяция задаётся экспертным путём.

2. Выбор родительской пары. Осуществляется для тех особей, для которых функция имеет максимальное значение.

3. Двухточечный кроссинговер. Случайным образом выбираются две точки разрыва i и j из диапазона [1, n-1]. Пусть при этом i<j. Тогда потомки определяются путем обмена соответствующих частей родительских хромосом:
   H1 = {c1₁, c1₂,.., c2_i, c2_i+1,.., c2_j, c1_j+1,.., c1_n},
   H2 = {c2₁, c2₂,.., c1_i, c1_i+1,.., c1_j, c2_j+1,.., c2_n}.

4. Мутация. Вероятность 10 %

5. Полученные особи-потомки добавляются в популяцию после переоценки.

Область притяжения для ЛА МИГ 29, описывается неравенствами

рад/с, м/с, (11)

рад, рад

Применив метод ГА и метод Хука-Дживса, получены следующие результаты:

Матрица А и В, найденная методом Хука-Дживса:

Матрица А и В, найденная методом ГА:

Результирующие матрицы:

В результате получили верхние и нижние значения границ обоих методов для результирующей матрицы. Для верхней границы использовалось максимальное значение из двух методов, также, для нижней границы выбрано минимальное значение из двух методов.

Метод генетического алгоритма эффективнее решает задачу построения интервальной матрицы, т.к. значения более приближенны к истинным.

Литература:

1. Бочкарёв А.Ф., Адреевский В.В. Аэромеханика самолёта–М: Изд-во Машиностроение, 1985.–357с.

2. Учебное пособие, Практическая аэродинамика самолёта МИГ-29 –М., 1995.– 316с.

3. Д. Гроп. Методы идентификации систем – М., 1978.

4. Остославский И. В. Аэродинамика самолёта – М., 1957. – 560с.: ил.

5. Исследование сложных технических систем на основе анализа областей притяжения / Р. Р. Акчурин, В. Н. Ефанов // 10-я Международная конференция по компьютерным наукам и информационным технологиям CSIT’2008: сб. науч. ст., Анталия, 2008, Т. 3. с. 131-136