Программное обеспечение и математическая реализация фрактального распознавания искусственных и природных объектов



Использование фрактальных сигнатур для задач обнаружения и идентификации различных целей является основой перспективных методов. Предложен адаптивный алгоритм для фрактального распознавания искусственных объектов, основанный на концепции сглаживания для правильной оценки фрактальной размерности в окрестности краев. Представлено описание модели в форме набора уравнений плоскостных кривых и показано, что такие признаки целей, как прямые линии, образующие силуэты, могут быть использованы для обнаружения объектов. Представлено экспериментальное сравнение результатов распознавания радиолокационных целей. Выявлено, что применение теории хаотических колебаний и фракталов весьма перспективно при обработке радиолокационных сигналов и идентификации радиолокационных целей.

Ключевые слова: фрактал, фрактальная сигнатура, коэффициент корреляции, фрактальная текстура, фрактальная размерность, бинарное изображение, фрактал контура единичной области, фрактальная обработка.

Современные подходы и средства в системе обработки информации (СОИ) повышают эффективность при решении задач мониторинга земной поверхности с помощью искусственных спутников Земли. Распознавание и автоматическое обнаружение протяженных малоконтрастных объектов на фоне земной и морской поверхности является одной из самых актуальных и трудных задач современных СОИ, при этом большая степень неопределенности при описании распределений вероятностей сигналов протяженных целей и помех окружающего фона приводит к проблемам при практической реализации существующих методов.

Объекты, построенные человеком, такие как промышленные и жилые здания, эффективно описываются набором простых геометрических примитивных фигур: кубов, сфер, цилиндров, конусов. Цветные же текстуры природного происхождения, являясь нерегулярными и фрагментарными, плохо поддаются такому описанию. При включении в систему геометрических признаков используются некоторые аппроксимирующие оценки в виде равновеликого эллипса рассеяния, размеров его большой и малой полуосей и тому подобное. Следовательно, для анализа таких текстур оказывается естественным представление их фракталами с некоторым размером фрактала D. До сих пор фактически нет окончательного определения фрактала. Концепция фракталов заключается в использовании самоподобия в определении размера фрактала [1].

В настоящее время фракталы применяются при анализе текстур ландшафтов, полученных при аэрокосмической съемке, поверхностей облаков, и других пористых сред и так далее. Однако размер фрактала цветной текстуры во многом зависит от выбора метода оценки. Так, при использовании разных методов оценки размера фрактала, можно получить соответственно и разные его размеры [1–2]. Итак, сопоставление текстур возможно при использовании одного и того же метода (группы методов). Более того не все текстуры хорошо различимы по размеру фрактала. Поэтому прежде чем включать в систему признаков размер фрактала, необходимо оценить фрактальность текстуры. Оценку фрактальности текстуры проводят на основе выбранного метода оценки размера фрактала. Поскольку размер фрактала вычисляется через оценку выборочной регрессии, то следует оценивать фрактальность текстуры по коэффициенту корреляции между логарифмом случайной величины и логарифмом заданной функции шага. При этом принятие решения о фрактальности текстуры можно строить следующим образом:

– построить зависимость коэффициента корреляции от шага; значение шага, при котором функция имеет максимум, является максимальным шагом в диапазоне задаваемых шагов при оценке размера фрактала;

– не учитывать оценку размера фрактала при низком коэффициенте корреляции в тех методах, где используется оценка фрактала как среднее значение в серии экспериментов;

– не включать размер фрактала в систему признаков для сегментации текстур при значениях коэффициента корреляции < 0,7.

Оценка фрактальности текстуры является важной характеристикой при сегментации по размеру фрактала. Алгоритм оценки размера фрактала текстуры по длине контура [1] состоит в развитии алгоритма оценки размера фрактала линии для оценки размера фрактала поверхности. Для оценки фрактала текстуры производится разбиение динамического диапазона яркостей изображения на равные интервалы. Для полученного набора пороговых уровней строится бинарное изображение. При этом значениям, яркость которых меньше порога, приписывается значение 0, а значениям, яркость которых выше или равна порогу, приписывается значение 1. Таким образом, исходное изображение представляется набором бинарных изображений. Для каждого из таких изображений производится оценка размера фрактала контуров единичных областей. В качестве оценки размера фрактала исходного изображения используется среднее значение полученных фракталов для бинарных изображений. При этом следует оценивать размер фрактала бинарных изображений только по строкам, только по столбцам, а также совместно по строкам и столбцам, что имеет особое значение при распознавании анизотропных текстур.

При использовании фрактальных сигнатур для определения объекта или природных текстур важно установить условия их независимости от размеров окна [2]. Неровности природных объектов могут меняться в различных масштабах. В [4] рассматривается четыре ИК-изображения (размером 256х190) двух классов облаков 1 (типа а, б) и 2

(типа а, б). Соответствующие фрактальные сигнатуры приведены на рис. 1. Следует отметить, что текстуры одной и той же категории дают в результате подобные сигнатуры.

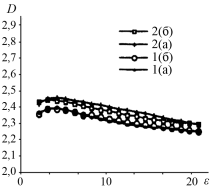
Рис. 1. Фрактальные сигнатуры четырех изображений двух классов облаков [4]

В исследованиях применялись три природные сцены в ИК и оптическом диапазонах: два класса облаков и лесной массив размером 64х64 [4]. Класс изображений облаков 1

(тип б) разделен на две вертикальные равные части. Соответствующие сигнатуры целого изображения и половинок (заштрихованные квадраты) показаны на рис.2,а. Все три сигнатуры достаточно точно совпадают друг с другом. Далее класс изображений облаков 2 (тип б) разделен на две горизонтальные и две вертикальные половины. Рассчитанные сигнатуры показаны на рис.2,б и рис.2,в. Фрактальные сигнатуры половинок изображений расположены вокруг сигнатуры полного изображения. Однако, сигнатуры левой и правой половинок изображения гораздо ближе к сигнатуре целого изображения, чем сигнатуры вертикальных половинок. Следовательно, левая и правая половинки изображения имеют более схожие текстуры, чем другие половинки. Сигнатуры полного изображения леса и верхней левой четверти изображения приведены на рис.2,г. Во всех примерах фрактальные сигнатуры относительно постоянны и слабо меняются при изменении масштаба.

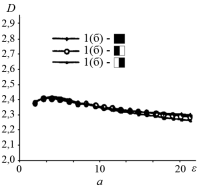
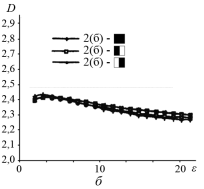
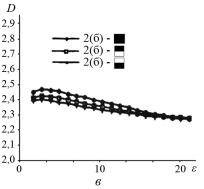
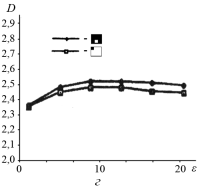
Рис. 2. Последовательность фрактальных сигнатур: а — класс 1 (тип б) изображений облака; б — класс 2 (тип б) изображений облака с их правыми и левыми половинами; в ‒ класс 2 (тип б) изображений с их верхними и нижними половинами; г ‒ изображение лесного массива

В предшествующих исследованиях считалось, что в окне имеется только интересующая нас единственная текстура, и нет кромок и антропогенных объектов. Однако, для фрактального распознавания искусственных объектов в [5] предложен адаптивный алгоритм, основанный на концепции кромкосохраняющего сглаживания для правильной оценки фрактальной размерности в окрестности краев. Для двух однородных областей в [3] экспериментально показано, что измеренная фрактальная размерность при всех масштабах меньше топологической размерности.

В то же время в [4] показано с использованием метода покрытий, что кромки проявляют себя как неровные поверхности при больших масштабах и имеют фрактальную размерность, превышающую топологическую. Для иллюстрации этого факта приведены результаты экспериментов с синтезированными и реальными изображениями.

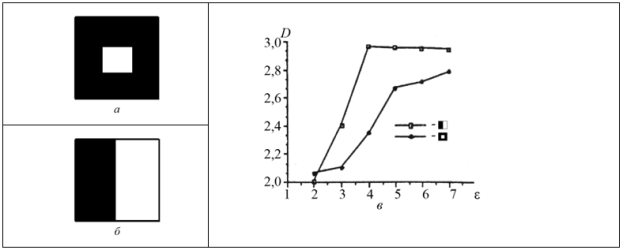
Рис. 3. Результаты экспериментов с синтезированными и реальными изображениями: а — изображение квадрата на черном фоне; б — ступенчатая кромка; в — фрактальные сигнатуры

На рис.3,а приведено изображение квадрата с геометрическим размером 32×32 пиксел на черном фоне с соответствующей фрактальной сигнатурой (рис.3,в). Изображение ступенчатой кромки и фрактальной сигнатуры представлено на рис.3,б и рис.3,в соответственно. Для обоих случаев неровности увеличиваются с возрастанием масштаба, и всегда значения D больше топологической размерности D0. Аналогичные результаты получены для реальных изображений горной местности.

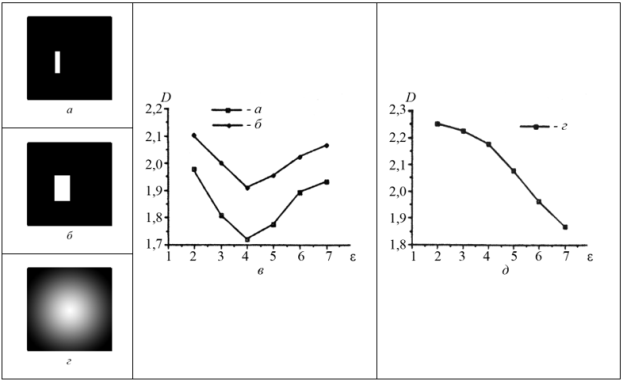
Рис. 4.Результаты исследования фрактальных сигнатур узких перепадов яркости на изображениях 32х32 пиксел: а — изображения узкого перепада яркости; б — широкого перепада яркости; г — дерево; в, д — фрактальные сигнатуры

В приведенных экспериментах условие D < D0 может иметь место для аномально малых образований. Иллюстрацией данного положения являются результаты исследования фрактальных сигнатур узких перепадов яркости на изображениях 32х32 пиксел, приведенные на рис.4. Вся сигнатура для узкого перепада яркости (рис.4,а) состоит из D < 2, а для более широкого перепада яркости (рис.4,б) это происходит только на некоторых масштабах. Для изображения дерева (рис.4,г) значение D < 2 наблюдается только при ε > 6 (рис.4,д).

Искусственные объекты состоят из относительно гладких частей, поэтому их фрактальные сигнатуры будут отражать гладкость на малых масштабах и неровность при больших ε. С учетом того, что фрактальные сигнатуры земных покровов относительно постоянны, возможно создание эффективных алгоритмов идентификации целей на фоне земной поверхности. Эксперименты в [4] проводились с тремя классами изображений (32х32 пиксел): растительный покров (море), деревья (островки), средства передвижения — машина (корабль) и два танка (две баржи). Соответствующие фрактальные сигнатуры приведены на рис.5.

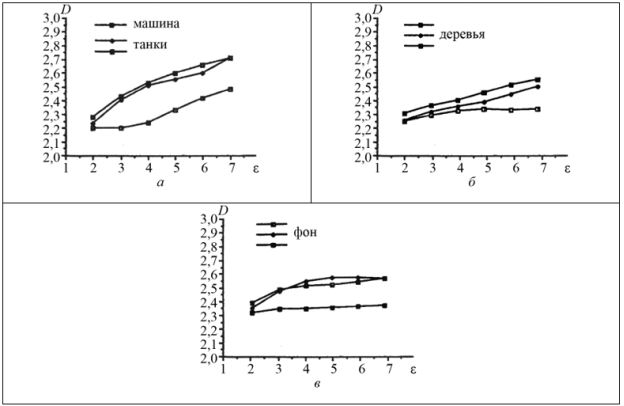
Рис. 5. Фрактальные сигнатуры для движущихся объектов: а — машина и танки; б — деревья; в — фон

Образцы изображений фона имели почти постоянные неровности в большинстве масштабов. Два из трех образцов обладали относительно большими значениями D. Для изображений деревьев фрактальная сигнатура имела слегка увеличивающийся наклон. Для изображений танков было отмечено резкое возрастание значений D при увеличении ε. Сигнатура машины более похожа на сигнатуру деревьев, чем на сигнатуру танков. Поэтому танки на фоне растительных покровов эффективнее обнаруживать по изменениям наклона фрактальных сигнатур.

Распознавание, основанное на использовании единственного масштаба, иллюстрируется в [4] на изображении зданий на склоне горы. Объекты типа зданий на изображении имеют более высокую яркость. Из-за «гладкой» структуры яркостного поля они обладают низким значением фрактальной размерности. При пороге разделения, равном 2,2 на шкале ε = 2, результаты фрактальной обработки позволяют выделить здания, ранее замаскированные фоном.

Одношкальное обнаружение танков между деревьями также было проведено в [4]. Результаты фрактальной обработки показали, что большинство образов танков сохранено на изображении при значительном снижении влияния земных помех. Фон частично сохранился, вследствие многомасштабности его характерных неровностей и размеров. Таким образом, использование фрактальных сигнатур для задач обнаружения и идентификации различных целей является основой многообещающих методов.

В [6, 8, 9] рассмотрен метод распознавания искусственных объектов на фоне природного пейзажа, основанный на модели фрактальности, т. е. системы характерных геометрических признаков. Представлено описание модели в форме набора уравнений плоскостных кривых и показано, что такие признаки целей, как прямые линии, образующие силуэты, могут быть использованы для обнаружения объектов. Приведены результаты экспериментальных исследований по выделению танков и морских судов на естественном фоне с помощью ИК датчика изображений и алгоритма фрактального оценивания. Применение теории хаотических и мультифрактальных колебаний для обработки радиолокационных сигналов при определении параметров цели и ее идентификации исследовано в [7]. Методом корреляционных интегралов получены оценки размерности эхо-сигналов от множественных целей. Рассчитаны показатели Ляпунова для пяти различных сечений, характеризующих сходимость результатов. Экспериментальное сравнение результатов распознавания радиолокационных целей показало, что применение теории хаотических колебаний и фракталов весьма перспективно при обработке радиолокационных сигналов и идентификации радиолокационных целей.

Литература:

1. Потапов А. А. Фракталы в радиофизике и радиолокации: Топология выборки. Изд. 2-е, перераб. и доп.- М.: Университетская книга, 2005.- 848 с.
2. Егорова Е. В., Бузылев Ф. Н., Нефедов В. И. Алгоритм обработки изображений. INTERMATIC-2009, ч. 4. Материалы Международной научно-технической конференции «Фундаментальные проблемы радиоэлектронного приборостроения», 7–11 декабря 2009 г. Москва, с. 138–139.Pentland A. P. Fractal-Based Description of Natural Scenes//IEEE Trans. 1984. V. PAMI-6, 6. P. 661–674.
3. Потапов А. А. Фракталы в дистанционном зондирование / Зарубежная радиоэлектроника. Успехи современной радиоэлектроники. 2000. № 6. С. 3–65.
4. Arduini F., Dambra C., Dellepiane S. et al. Fractal Dimension by Adaptive Mask Selection//Proc. IEEE Intern. Conf. on Acoustics, Speech and Signal Processing. — N. Y.: 1988. P. 1116–1119.
5. Аксяитов М. Х., Егорова Е. В., Мартынов Н. В., Рыбаков А. Н. Обнаружение малоконтрастных целей, Успехи современной радиоэлектроники № 1, 2017, стр. 23–26
6. Xion M., Zhuang Z., Xiao S., Guo G. The Analyse and Recognition of Radar Targets Scattering Signal with Chaos Multifractal Theory//J. National University of Defense Technology (China). 1998. V. 20, 2. P. 60–64.
7. Реконструкция изображений/Под ред. Г. Старка: Пер. с англ.; Под ред. Б. С. Кругликова. — М.: Мир, 1992. С.636.
8. Фор А. Восприятие и распознавание образов: Пер. с франц.; Под ред. Г. П. Катыса. — М.: Машиностроение, 1989. С.272.
9. Карпов М. А., Сигов А. С., Попов Е. А., Нефедов В. И. Методы исследования изображений в нестационарной спектроскопии. // Наукоемкие технологии. — 2011, № 7, т. 12, с. 4–59.