Алгоритмическая реализация обработки спектрального анализа



Нахождение уровня корреляционным методом сводится к вычислению взаимной корреляционной функции сигналов, поступающих с датчиков. Однако на практике, так как размер исследуемых выборок достаточно велик, использование (1):

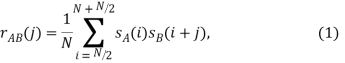
для вычисления корреляционной функции не является целесообразным. Очевидно, что реализация (1) требует умножения каждого отсчета последовательности , на каждый из отсчетов последовательности , то есть операций умножения. Так как величина оказывает влияние на точность обнаружения уровня, она является достаточно большой (имеет порядок десятков тысяч), что затрудняет расчет корреляции непосредственно.

Таким образом, для больших более эффективным способом расчета корреляционной функции является использование алгоритма Тома-Кука. В основу алгоритма положена теорема о корреляции, которая описывается следующим соотношением

где — прямое дискретное преобразование Фурье (ДПФ); — обратное ДПФ; — комплексно-сопряженное представление результатов прямого ДПФ. Преимущество (2) заключается в возможности использования эффективных алгоритмов ДПФ, для вычисления взаимной корреляционной функции. В частности, использование алгоритма быстрого преобразования Фурье (алгоритма Кули-Тьюки), позволяет ускорить расчет по формуле (2) для . Это связано с более благоприятной асимптотикой метода — количество необходимых операций умножения в данном случае составляет . Кроме того, специфика расчета ДПФ с помощью алгоритма БПФ позволяет производить его эффективную реализацию на многопроцессорных устройствах, что позволяет получить существенный выигрыш в быстродействии системы обработки сигналов в целом.

При программной реализации, алгоритм Тома-Кука может быть представлен следующей последовательностью шагов:

Шаг 1. С помощью алгоритма БПФ выполняются дискретные преобразования Фурье дискретизированных сигналов обоих датчиков:

Так как применение БПФ связано с последовательным делением точечной последовательности на две точечных и далее, то на количество отсчетов в исходной последовательности накладывается ограничение , где — целое. Кроме того отсчеты сигналов и являются вещественными, следовательно ДПФ содержит 2 вещественных спектральных отсчета и комплексно сопряженных пар отсчетов. В связи с этим, результат БПФ может быть представлен уникальным спектральным отсчетом, то есть .

Шаг 2. Путем поэлементного перемножения и формируется новый комплексный массив (кросс-спектр сигналов):

Шаг 3. С помощью алгоритма БПФ выполняется обратное дискретное преобразование Фурье кросс-спектра сигналов датчиков:

Результатом обратного ДПФ является функция взаимной корреляции , где .

Шаг 4. В связи с тем, что использование аппарата ДПФ предполагает - периодичность исходных последовательностей, то функцию взаимной корреляции , также можно считать — периодической. В связи с этим справедливо следующее представление корреляционной функции:

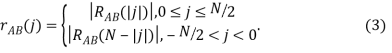
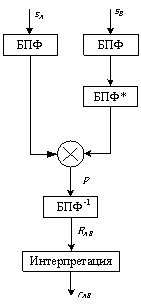
Рис. 1. Схема вычисления взаимной корреляции через БПФ

Для измерения уровня в емкости разработаем программу, задача которой спектральный анализ принятого сигнала. На вход программы поступает звукозапись, размер окна, начальный индекс, вектор гармоник и вектор окрестностей:

Рис. 2. Тело программы вычисления спектрального анализа

Алгоритм программы такой:

1. достаём окно сигнала (размер задается на входе);
2. находим сначала его комплексный спектр;
3. получаем из него амплитудный спектр;
4. дальше считаем энергию принятого сигнала в заданных частотных областях (учитывая окрестности);

На входе функции соответственно: I — запись сигнала (одноканального), в нашем случае, определять значение функции будем два раза для верхнего и нижнего датчиков соответственно;

II — частота дискретизации — частота взятия отсчётов непрерывного по времени сигнала при его дискретизации (в частности, аналого-цифровым преобразователем), со звуковой карты — 44.1 кГц — используется в Audio CD. Выбрано Sony из соображений совместимости с стандартом PAL, за счёт записи 3 значений на линию картинки кадра × 588 линий на кадр × 25 кадров в секунду, и достаточности (по теореме Котельникова) для качественного покрытия всего диапазона частот, различаемых человеком на слух (20 Гц — 20 КГц); III — ширина окна БПФ (кратна двойки) и ровна ; IV — начальный индекс, с которого начинаем разбирать запись (то есть, чтобы не разбивать запись предварительно, можно было взять окно откуда-нибудь из середины); V — вектор, содержащий индексы спектральных отсчётов, в котором мы ищем гармоники (набор гармоник выходного сигнала динамика):

;

VI — вектор, где для каждой гармоники указана окрестность, в которой мы её ищем.

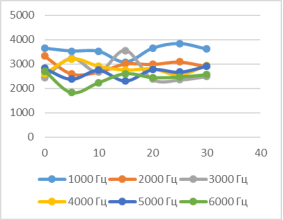
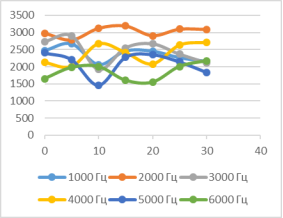
Верхний датчик Нижний датчик

Литература:

1. Method and apparatus for detecting and locating fluid leaks / patent US 4083229 A. — 1978.
2. Мясниикова Н. В., Берестень М. П., Цыпин Б. В., Мясникова М. Г. Экспресс-анализ сигналов в инженерных задачах // Физматлит, 2016. — С. 184.
3. Александр Харкевич. Спектры и анализ // Editorial URSS, 2018. — C. 240.
4. Айфичер Э. С., Джервис Б. У. Цифровая обработка сигналов: практический подход. 2-е изд. — М: Вильямс, 2008. — 992 с.
5. Методы спектрального анализа в задаче обнаружения аномалий информационных процессов телекоммуникационных сетей. — М.: Бибком, 2013. — 171 с.