Математическая основа алгоритма определения неисправности датчиков по их выходным данным

Одним из факторов, определяющих достоверность результатов, получаемых при обработке результатов измерений датчиков, является наличие возможности фильтрации неточных значений. Неточные значения могут появляться в результате помех в канале связи, неисправности приемной, передающей и измерительной аппаратуры.

Неисправность датчика, как и его цепей, является частным случаем сбоев измерительного тракта. Необходимость автоматического контроля (т.е. с помощью программных или программно-аппаратных средств) исправного состояния датчика по его показаниям следует из того, что, как правило, отсутствуют дополнительные вспомогательные данные об исправности датчика, а устанавливать непосредственный контроль за измерительным оборудованием нет возможности. Неавтоматический контроль с помощью человека потребует больших материальных и ресурсных затрат. При этом именно такую неисправность сложнее всего определять автоматически. Это связано с необходимостью очень точно задать критерии корректной работы датчика, такие как возможные допуска на значения измеряемого параметра и временные интервалы для соответствующих допусков. Для определения неисправности датчиков можно использовать статистические данные, собранные при предыдущих аналогичных измерениях с помощью таких же датчиков.

При сборе статистики следует учитывать, что результаты двух различных измерений какого-либо параметра одного и того же физического процесса могут иметь различаться как по величине значений, так и по моменту времени характерных изменений в измеряемом параметре. Основными причинами таких различий как правило являются внешние воздействия на систему, в которой происходит процесс, начальные условия процесса или воздействия компонентов системы на ход процесса. Однако в целом поведение параметров физического процесса носит сходный характер.

Для статистической оценки поведения параметра удобно использовать его дисперсию[1]

, (1)

среднеквадратичное отклонение (СКО)[1]

, (2)

а также математическое ожидание[1]

, (3)

где

. (4)

Как известно

. (5)

Полагая на некотором интервале значений размера все из (5) и (3) получим

, (6)

где – среднее арифметическое значение измеряемого параметра на интервале размера .

Тогда из (1) и (2) следует

, (7)

(8)

Данные вычисления ((6), (7), (8)) следует производить на небольших интервалах, разбивая весь интервал значений параметра на интервалов размера . Если производить вычисления на слишком большом (в частности при , т.е. на всем интервале значений параметра) или слишком маленьком интервале то результаты могут оказаться некорректными. При слишком малом интервале дисперсия и математическое ожидание будут неточны, при слишком большом будут учитывать все изменения значений параметра, что не позволит обнаружить отклонения значений от ожидаемых.

При таких способах оценки точности телеизмерений математическое ожидание является лишь вспомогательным критерием. Использование его как основного наложит существенные ограничения, т.к. любое отклонение состояния системы от того, при котором рассчитывалось математическое ожидание, приведет к отклонению значений от ожидаемых. Использование дисперсии и СКО устраняет данное ограничение.

При статистическом анализе следует учитывать характер поведения измеряемого параметра физического процесса: так, например, на вибрационных параметрах как правило допускается дисперсия большей величины, чем на температурных параметрах, многие параметры предполагают изменение значений математического ожидания и дисперсии во времени. Для учета характера поведения удобно производить анализ дисперсии, СКО и математического ожидания первой[2]

, (9)

и второй производной значений телеметрического параметра

. (10)

Такой подход позволит отличить изменение значений параметра в результате изменения измеряемой величины от изменения в результате действия помех или прочих факторов. Без такого анализа необходимо строго оценивать временные интервалы возможных изменений статистических характеристик телеметрируемых параметров.

Для автоматического определения неисправности датчика путем анализа его показаний предлагается методика, описанная далее.

Сигнал на приемной стороне состоит из нескольких компонентов (11):

• непосредственно сигнала датчика,

• белого шума датчика ,

• белого шума и помех в линии передачи данных, шума приемного и передающего устройства .

(11)

Белый шум присутствует в составе сигнала постоянно, но шум в линии передачи данных может компенсироваться помехоустойчивым кодированием и самим способом передачи (правильный выбор мощности, ширины полосы, модуляции сигнала). Шум датчика и шум в линии передачи, входящей в состав системы на которой проводятся измерения сложно компенсировать без использования инновационных методов: интеллектуальных датчиков, оптоволоконных бортовых линий связи и датчиков с оптическим выходом (такие методы позволяют дополнительно защитить сигнал от действия помех). Белый шум в силу своей физической природы вносит почти одинаковые искажения в принимаемый сигнал вне зависимости от внешних условий и состояний системы.

Помехи в линии связи (при их наличии) вносят сложнокомпенсируемое искажение в принимаемый сигнал, но их воздействие в большинстве случаев кратковременно.

Во время устойчивого приема сигнала , при этом «. При неустойчивом приеме значительно возрастает. Как написано выше, может различаться при одинаковых характеристиках физического процесса в системе вследствие внешних воздействий на систему.

Дисперсия принимаемого сигнала, аналогично формуле (11) состоит из нескольких компонентов:

, (12)

но для медленно меняющихся параметров , для быстроменяющихся параметров это условие справедливо при больших помехах в линии.

Следовательно, для каждого параметра можно задать некоторые значения и на определенных интервалов времени ( может быть велико), при которых выполнение условия (13) будет свидетельствовать о высокой точности измерений параметров физического процесса.

. (13)

Нарушение этого условия может свидетельствовать о высоком уровне помех в канале связи () или некорректной работе измерительного оборудования (датчика), например в результате образования ложного спая (неравенство может нарушаться как в одну, так и в другую сторону).

Дисперсии первой и второй производных тоже удовлетворяют аналогичным условиям (14), (15). Использование производных более точно позволяет идентифицировать нештатные отклонения значений измеряемых параметров.

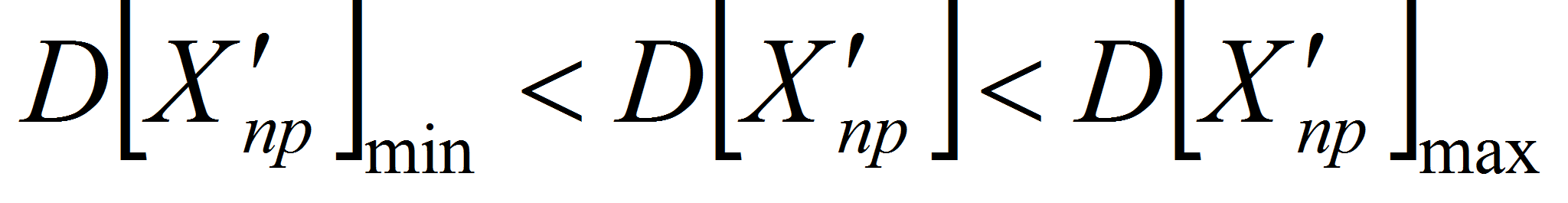(14)

(15)

Таким образом, оценка попадания дисперсии измеряемого параметра и дисперсии его производных, а также математических ожиданий параметров и их производных (в качестве дополнительных критериев) позволяет составить алгоритм для автоматического детектирования неисправности датчиков, а также наличия сбоев в канале передачи данных. Алгоритм может быть реализован программно (реализован в компьютерной программе) или программно-аппаратно (реализован в микроконтроллере или программируемой логической интегральной схеме). Суть алгоритма сводится к вычислению значений вышеуказанных характеристик параметра и сравнению их с граничными значениями, заданными на основе статистики предыдущих измерений аналогичного параметра. По итогам сравнений программа может сделать вывод о корректности значений параметра (или некорректности с указанием временных интервалов со сбойными значениями параметра). При этом отсутствует необходимость оператору самостоятельно анализировать значения параметров (или графики значений параметров) на предмет выявления неисправностей датчиков и их цепей.

Литература:

1. Г. Корн, Т. Корн Справочник по математике для научных работников и инженеров. М., 1973 г., 832 стр. с илл.

2. Бронштейн И.Н ., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов. – 13-е изд., исправленное. – М.: Наука, Гл. ред. Физ.-мат. лит., 1986. –544с.