Математическое моделирование параллельного компенсатора мощности

В настоящее время по оценкам отечественных и ведущих зарубежных специалистов, доля энергоресурсов, и в частности электроэнергии, составляет порядка 30-40% от стоимости продукции [1, с.6]. Полная мощность, потребляемая нагрузкой, делится на две составляющие – активную и реактивную. Реактивная мощность в отличие от активной не совершает механической работы, тем не менее, она необходима для работы реактивной нагрузки. Вследствие этого целесообразно локализовать место ее протекания непосредственно вблизи с оборудованием, поскольку при этом снижаются потери мощности на проводах и кабелях, появляется возможность подключения дополнительной нагрузки за счет снижения тока, потребляемого с силового трансформатора. Локализация протекания реактивной составляющей полной мощности лежит в основе компенсации реактивной мощности. Поэтому этот метод является одним из направлений решения вопроса энергосбережения. Меры принимаемые для компенсации реактивной мощности, помимо снижения затрат на электроэнергию увеличивают ресурс оборудования, тем самым уменьшая расходы компании или производства.

Одним из мероприятий по компенсации реактивной мощности является параллельное подключение к устройству с постоянной нагрузкой компенсирующего конденсатора соответствующей мощности. При изменяющейся во времени нагрузке рекомендуется использовать автоматические конденсаторные установки. Однако при этом процесс компенсации происходит не единовременно с изменением параметров сети, а с некоторой задержкой. Применение конденсаторных установок с переключающими ключевыми полупроводниковыми элементами (тиристорами) приводит к появлению переходных процессов, ухудшающих качество сетевого напряжения. Не маловажным фактором является то, что подобные компенсаторы не обеспечивают компенсации реактивной мощности в нагрузке по высшим гармоникам.

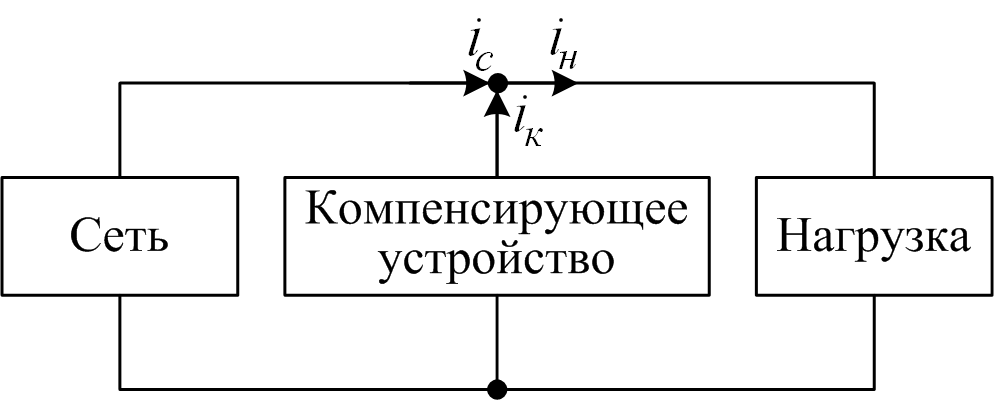
Рассматриваемый в статье параллельный компенсатор реактивной мощности отличается отсутствием данных недостатков. На рисунке 1 приведена структурная схема включения исследуемого компенсатора.

Рис. 1. Структурная схема системы с параллельным компенсатором

Особенностью системы, изображенной на рисунке 1, является то, что искажения, вносимые нагрузкой в сетевой ток, компенсируются включенным параллельно нагрузке компенсирующим устройством. Это устройство генерирует ток компенсации , таким образом, что ток сети становится сфазированным с сетевым напряжением и равным активной составляющей тока нагрузки . Алгоритм вычисления тока компенсации представляет собой следующую последовательность действий:

1) Вычисляется активная мощность нагрузки из измеренных тока нагрузки и напряжения нагрузки за текущий период :

. (1)

2) Вычисляется активное сопротивление нагрузки и активный ток через нагрузку за этот же период :

; (2)

, (3)

где – действующее сетевое напряжение (равное действующему напряжению на нагрузке ).

3) Вычисляется ток компенсации на следующий период:

. (4)

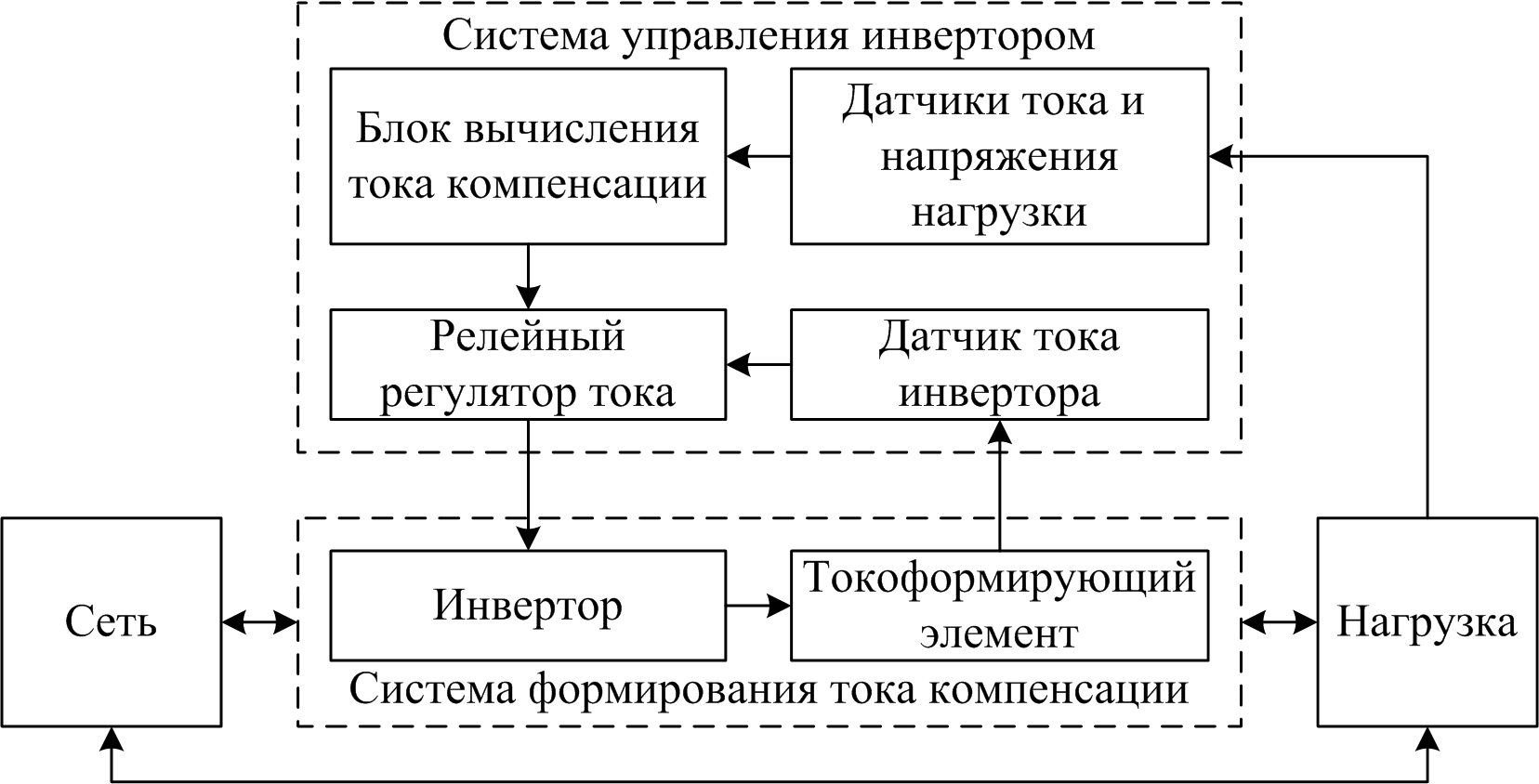
Структурная схема компенсирующего устройства, выполняющего данный алгоритм и формирующего ток компенсации, представлена на рисунке 2.

Рис. 2. Структурная схема компенсирующего устройства параллельного типа

Схема работает следующим образом:

1. информация о текущих значениях напряжения и тока нагрузки с датчиков поступают в блок вычисления тока компенсации;

2. в блоке вычисления тока компенсации по алгоритму, описанному выше, производится вычисление тока компенсации;

3. релейный регулятор тока (РРТ) по вычисленному току компенсации и информации о реальном токе, полученной от датчика тока инвертора, формирует импульсы управления на силовых ключах инвертора;

4. силовые ключи инвертора отрабатывают протекание через токоформирующий элемент вычисленного тока компенсации.

Для исследования системы с параллельным компенсатором реактивной мощности использовалась среда математического моделирования MATLAB и ее модуль Simulink, позволяющий моделировать, имитировать и анализировать динамические электрические системы.

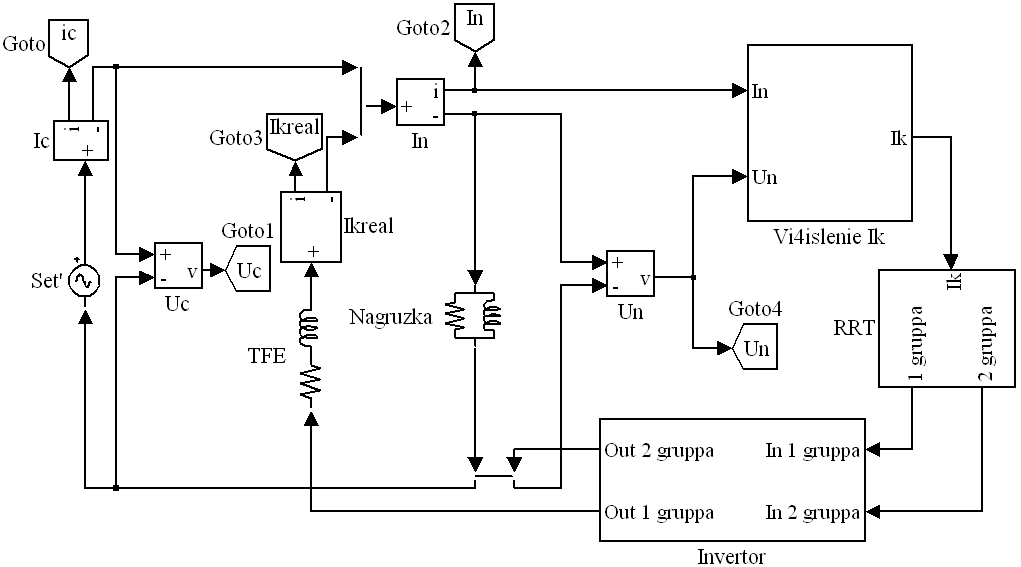
На рисунке 3 представлена расчетная модель системы с параллельным компенсатором, разработанная в пакете MATLAB.

Рис. 3. Расчетная модель исследуемой системы в программе MATLAB

Сеть (блок Set’) моделируется источником переменного напряжения с действующим значением равным 220 В. Нагрузка (блок Nagruzka) представляет собой параллельно включенное сопротивление R = 10 Ом и индуктивность L = 15 мГн. Токоформирующий элемент (блок TFE) представляет собой индуктивность L = 10 мГн с собственным сопротивлением R = 0,1 Ом.

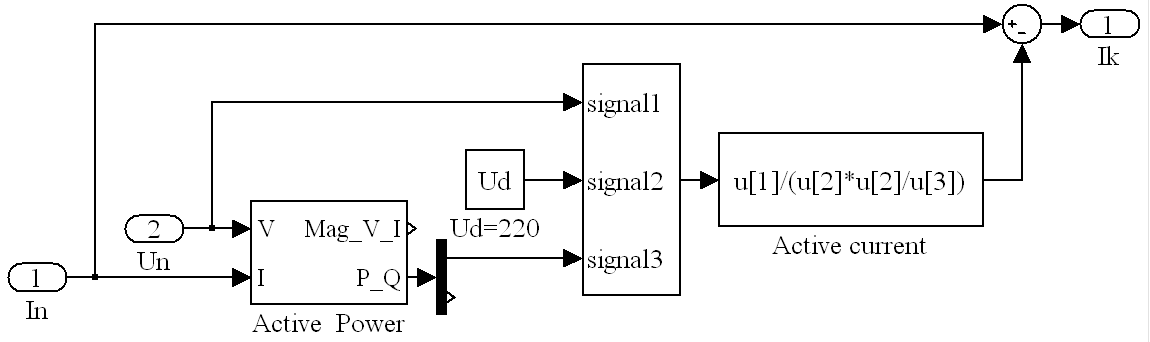
Рассмотрим более подробно устройство остальных блоков и принцип их работы. На рисунке 4 представлена схема блока вычисления тока компенсации (блок Vi4islenie Ik на рисунке 3).

Рис. 4. Схема блока вычисления тока компенсации

Данный блок реализует алгоритм вычисления тока компенсации. На входы 1 (In) и 2 (Un) подаются соответственно ток и напряжение нагрузки, блок Active Power вычисляет значение активной мощности за период. Значения напряжения сети Un, действующего напряжения сети Ud и мощности в блоке Active current служат для вычисления активного тока по формулам (2) и (3) приведенным к одному уравнению. Блок вычисления разницы реализует формулу (4) и на выходе получается вычисленный ток компенсации.

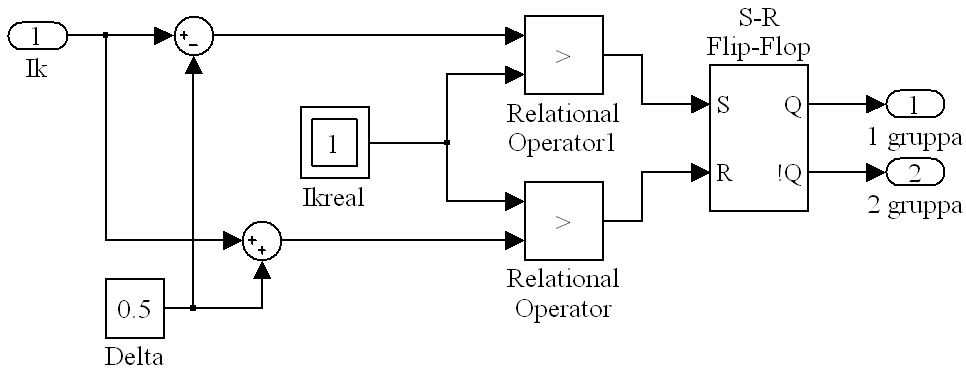
Рассмотрим теперь блок релейного регулятора тока (блок RRT на рисунке 3), схема которого приведена на рисунке 5.

Рис. 5. Схема блока релейного регулятора тока

Она представляет собой релейный регулятор тока с двумя фиксированными состояниями. Условиями переключения ключей является достижение реальным током компенсации (блок Ikreal) одного из пределов погрешности  (задана в блоке Delta) установленного от значения вычисленного тока компенсации. Этот ток поступает на вход 1 (Ik) с выхода 1 (Ik) блока вычисления тока компенсации (рисунок 4). За пересечением верхней и нижней границ следят компараторы (блоки Relational Operator и Relational Operator1 соответственно).

Таким образом, при условии , т.е. при превышении верхней границы реальным током компенсации, с компаратора (блок Relational Operator) на R вход триггера (блок S-R Flip-Flop) подается логическая единица. Состояние прямого выхода триггера переходит в состояние логический ноль, а инверсного в логическую единицу. При этом силовые ключи VT1 и VT3 закрываются, а ключи VT2 и VT4 открываются (силовые ключи изображены на рисунке 7). При достижении условия , с выхода компаратора (блок Relational Operator1) логическая единица поступает на S вход триггера. Состояние прямого выхода триггера переходит в состояние логическая единица, а инверсного в логический ноль. Силовые ключи VT1 и VT3 открываются, а ключи VT2 и VT4 закрываются.

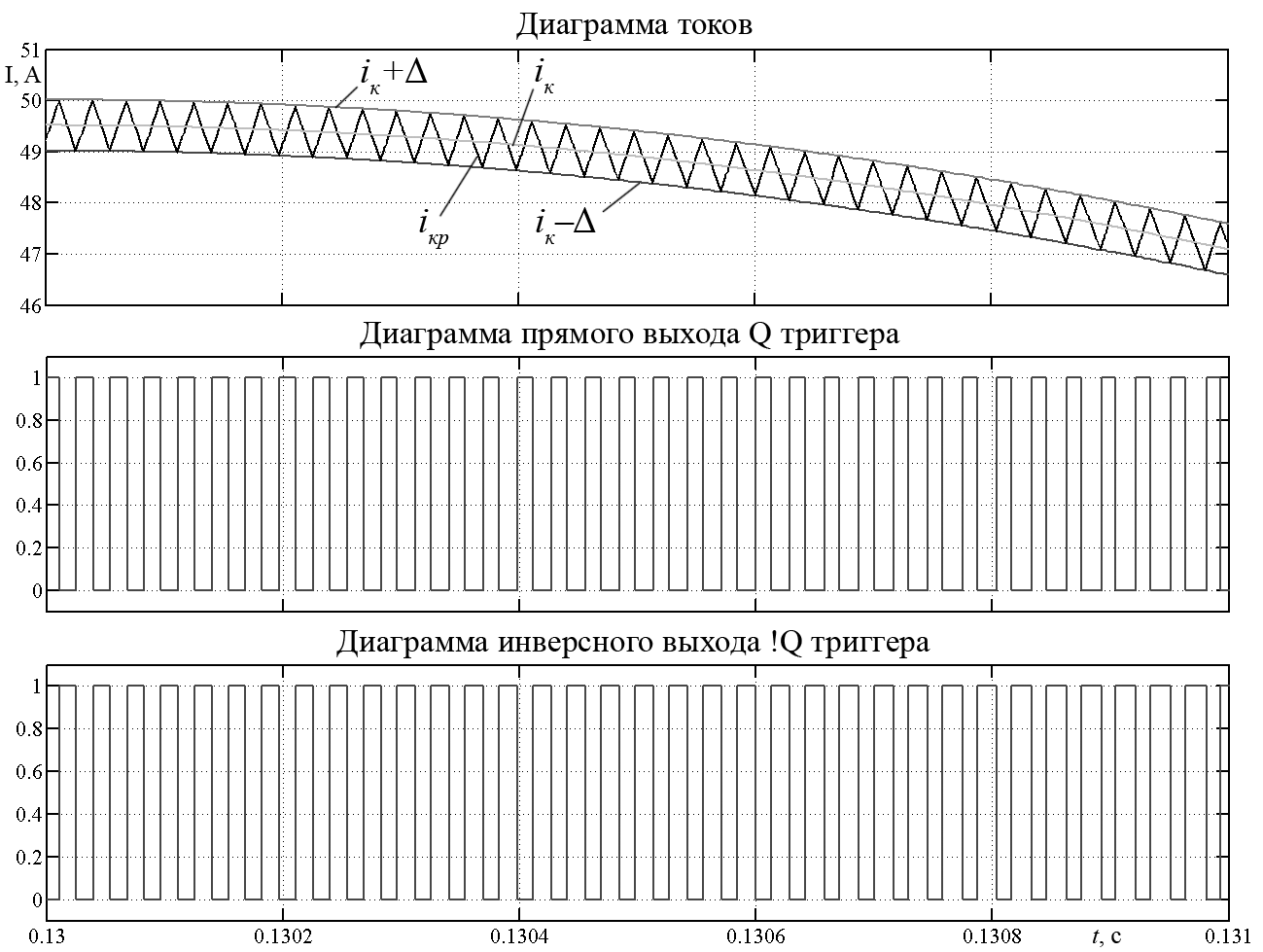
Наглядно работу релейного регулятора тока видно на диаграммах токов и состояний выходов триггера (рисунок 6).

Рис. 6. Диаграммы, поясняющие принцип работы релейного регулятора тока

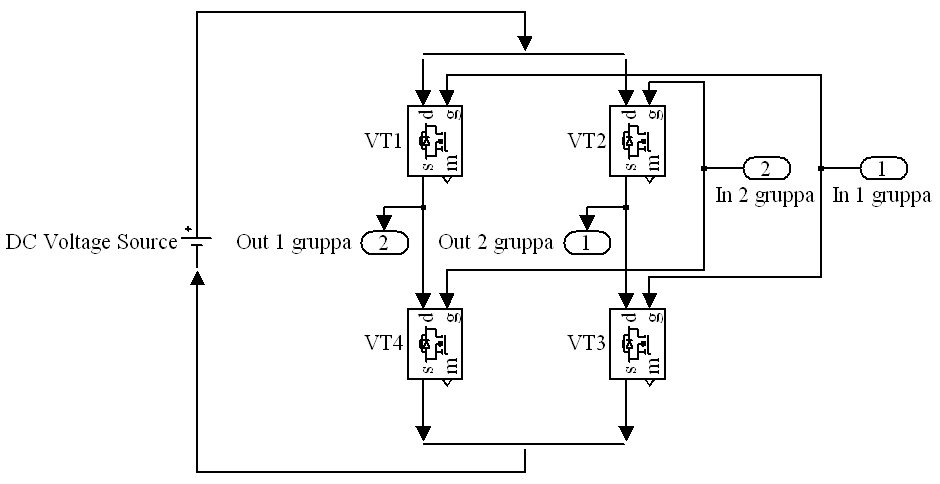
Структура инвертора (блок Invertor на рисунке 3) представлена на рисунке 7. Она включает управляемые силовые ключи (VT1 – VT4), включенные по мостовой схеме, и источник питания инвертора, выполненный постоянным источником ЭДС (DC Voltage Source).

Рис. 7. Схема инвертора

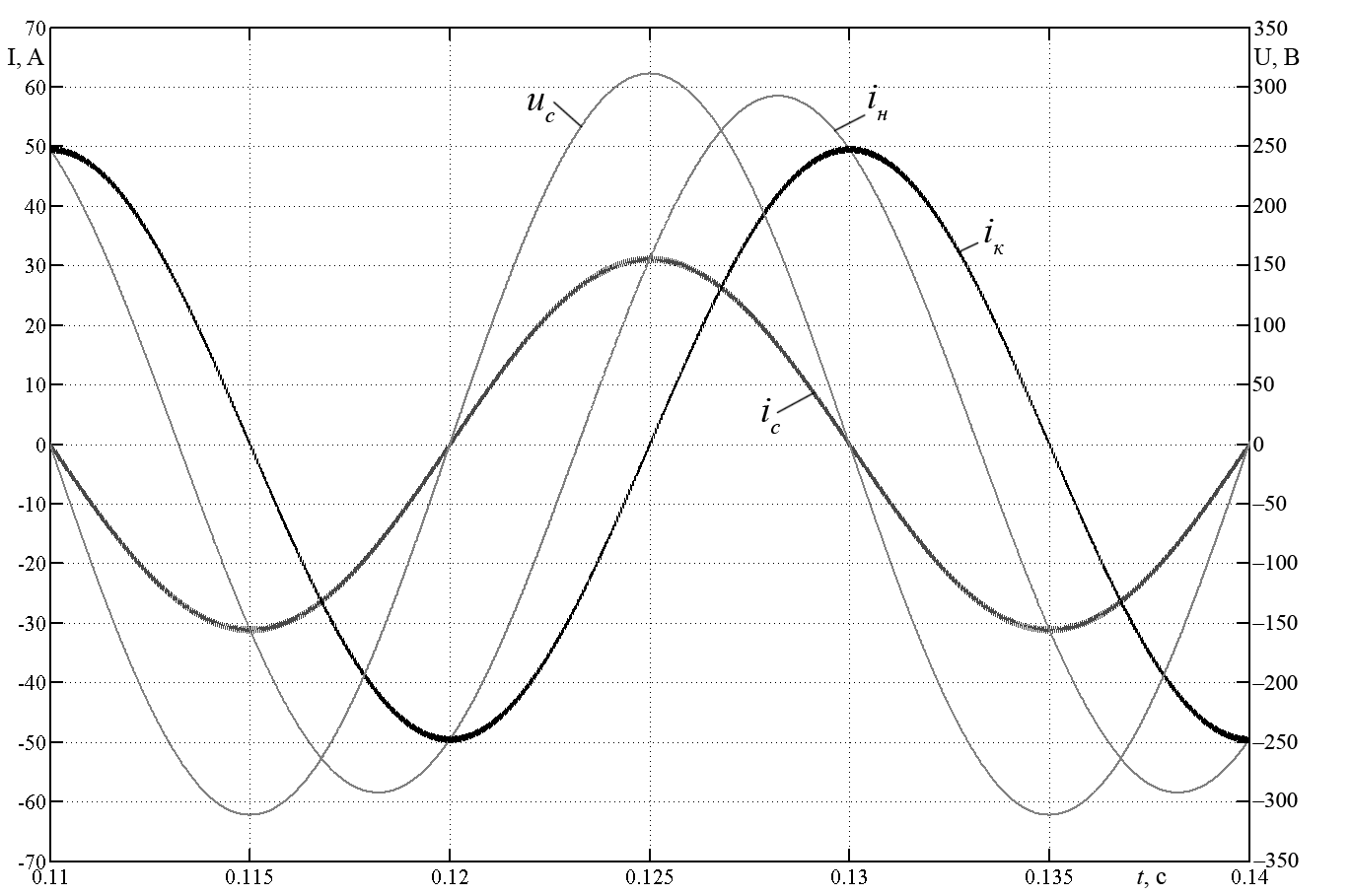
Проведем анализ результатов моделирования по диаграмме, полученных напряжения сети, токов сети, нагрузки и компенсации (рисунок 8).

Рис. 8. Диаграмме напряжения сети, токов сети, нагрузки и компенсации

На диаграмме можно графически увидеть разницу тока нагрузки и сетевого тока в виде тока компенсации. Это говорит о выполнении формулы (4). Приведенные кривые тока и напряжения сети показывают, что они сфазированны и нагрузка потребляет из сети только активную составляющую мощности.

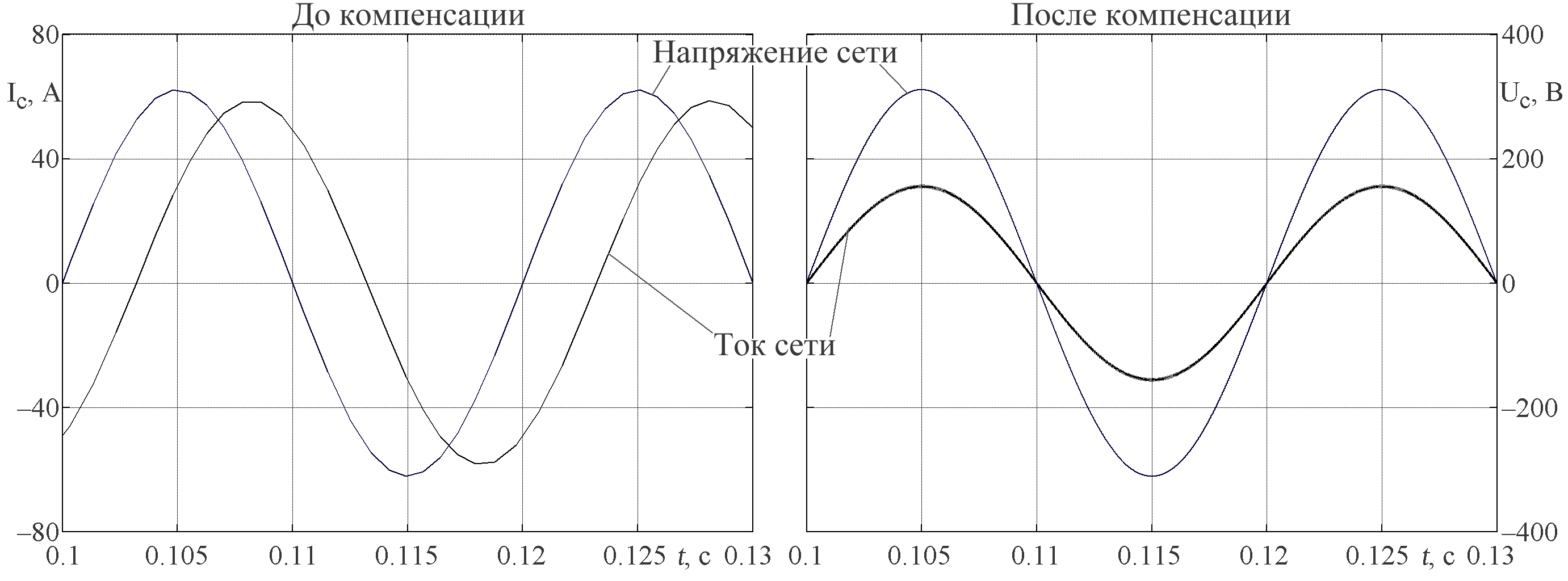
На рисунке 9 представлены диаграммы токов и напряжения сети, иллюстрирующие результат работы компенсирующего устройства.

Рис. 9. Сравнение напряжения и тока сети до компенсации и после

На левом графике можно видеть сдвиг по фазе между напряжением и током сети, а на правом благодаря работе компенсатора они становятся сфазированными. Также можно наблюдать, что за счет отсутствия в токе сети реактивной составляющей мощности протекающей в нагрузке, уменьшается и амплитуда сетевого тока, а следовательно и потребляемая полная мощность.

Отметим, что возможен режим работы инвертора, генерирующий частично или полностью активный ток нагрузки, а также режим, в котором энергия от источника ЭДС поступает в сеть. Такие режимы возможны при замене постоянного источника ЭДС альтернативным источником энергии и модификацией системы управления инвертором. Подобная альтернатива является одной из основных задач для дальнейшего исследования системы с параллельным компенсатором.

Полученные результаты позволили сформировать список проблем и действий для их решения:

1. Наличие высших гармоник в компенсационном токе и вызываемых ими высших гармоник в сетевом токе.

2. Определение условий работы инвертора в режиме генерации энергии от источника ЭДС в нагрузку и сеть.

3. Исследование работы системы совместно с альтернативным источником энергии.

Литература:

1. http://www.matic.ru/doc/brochure/parts/teor.pdf