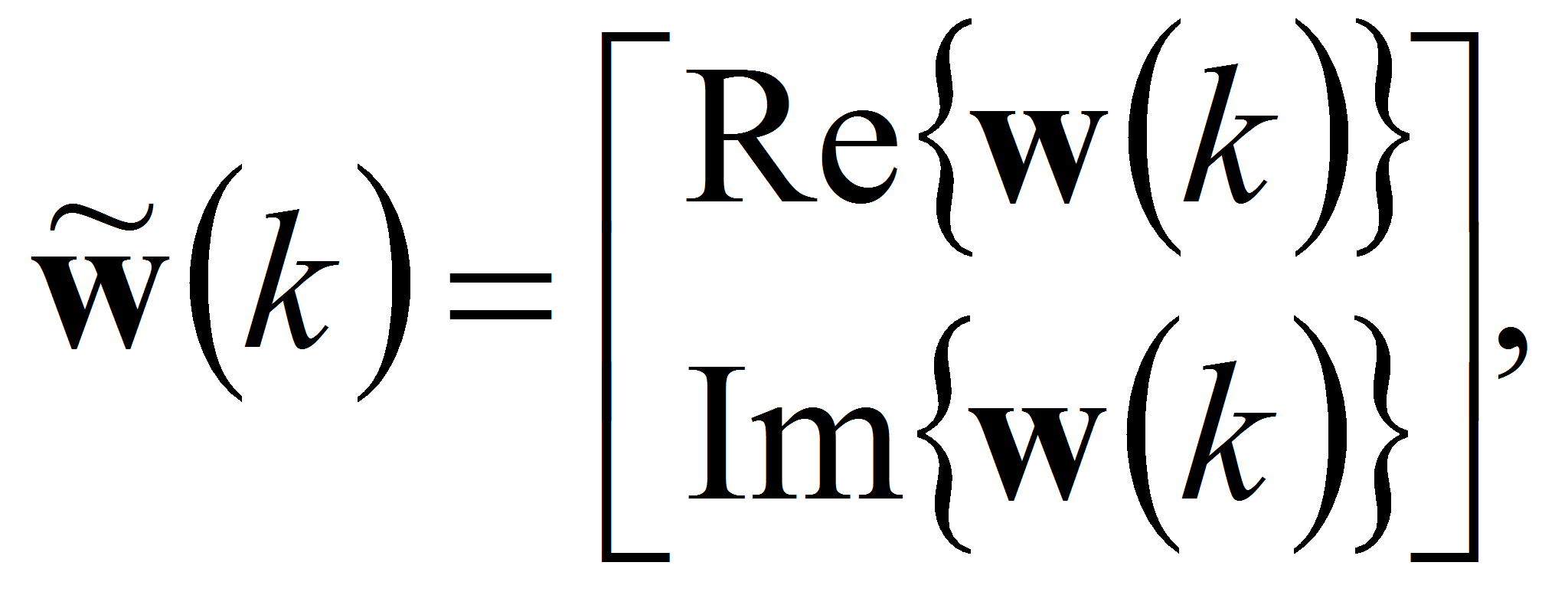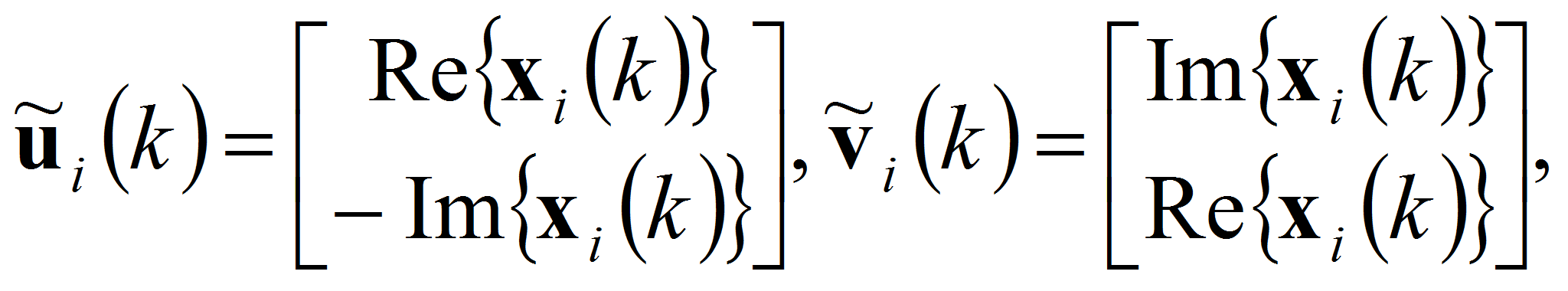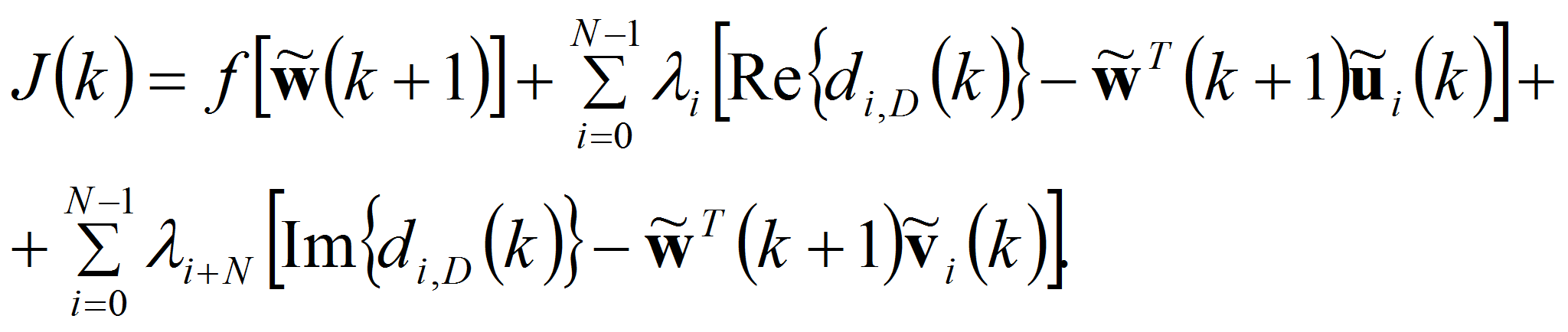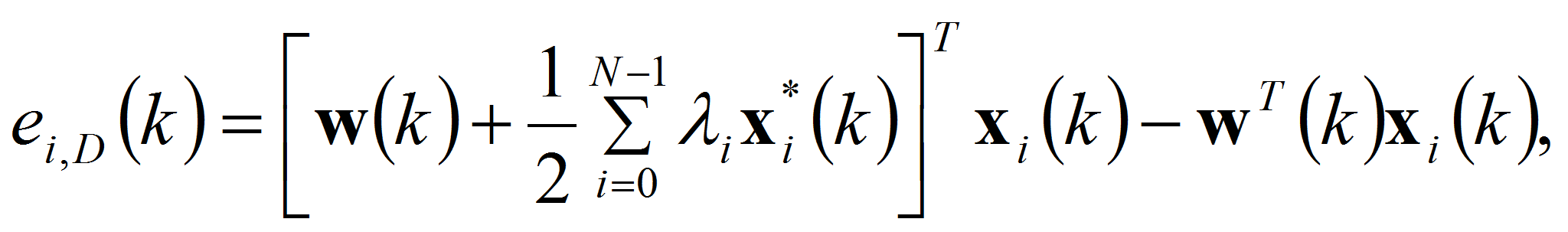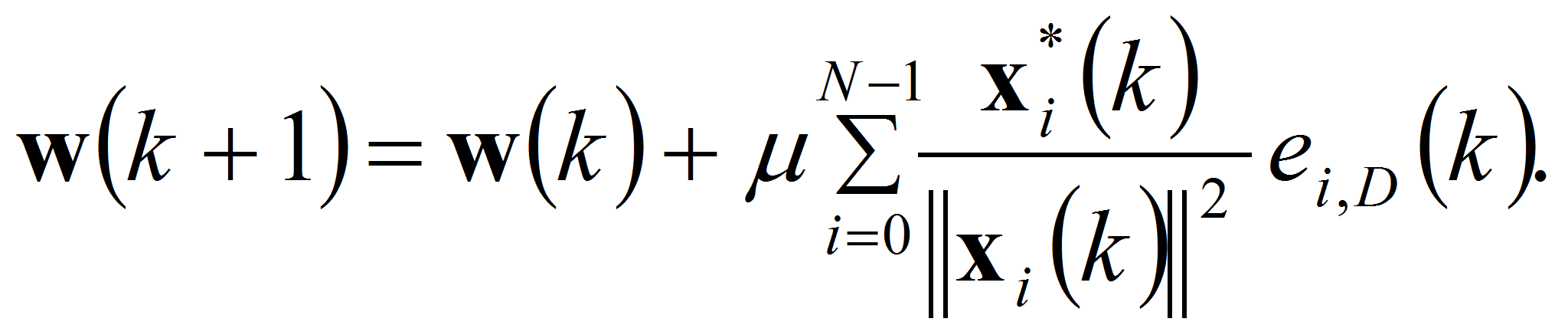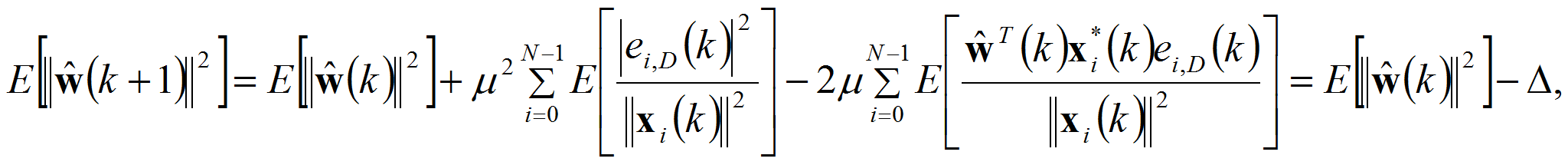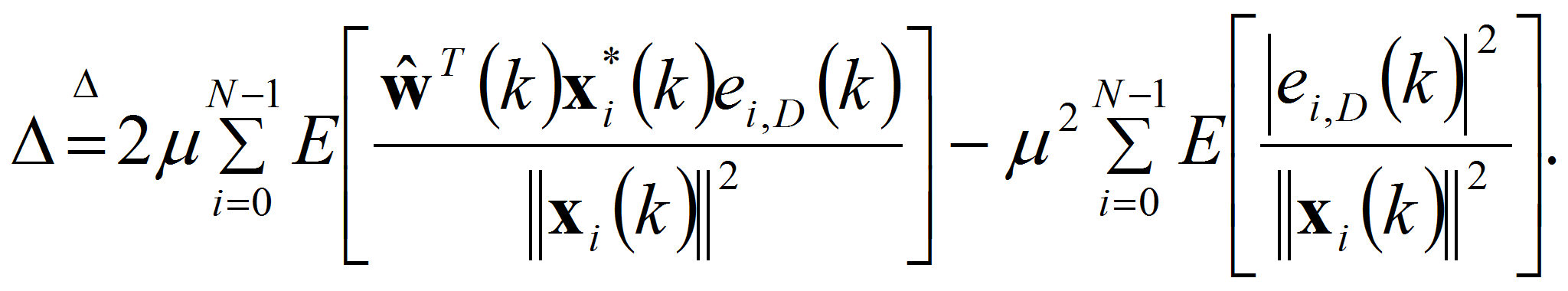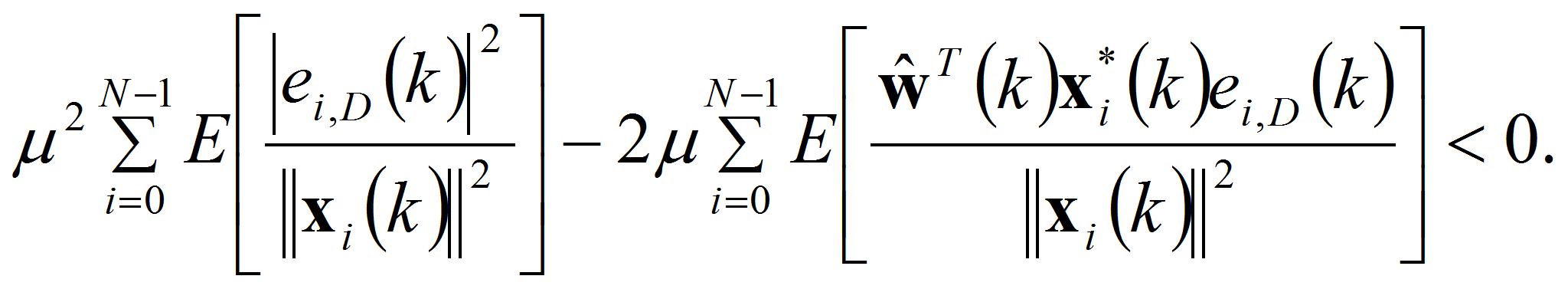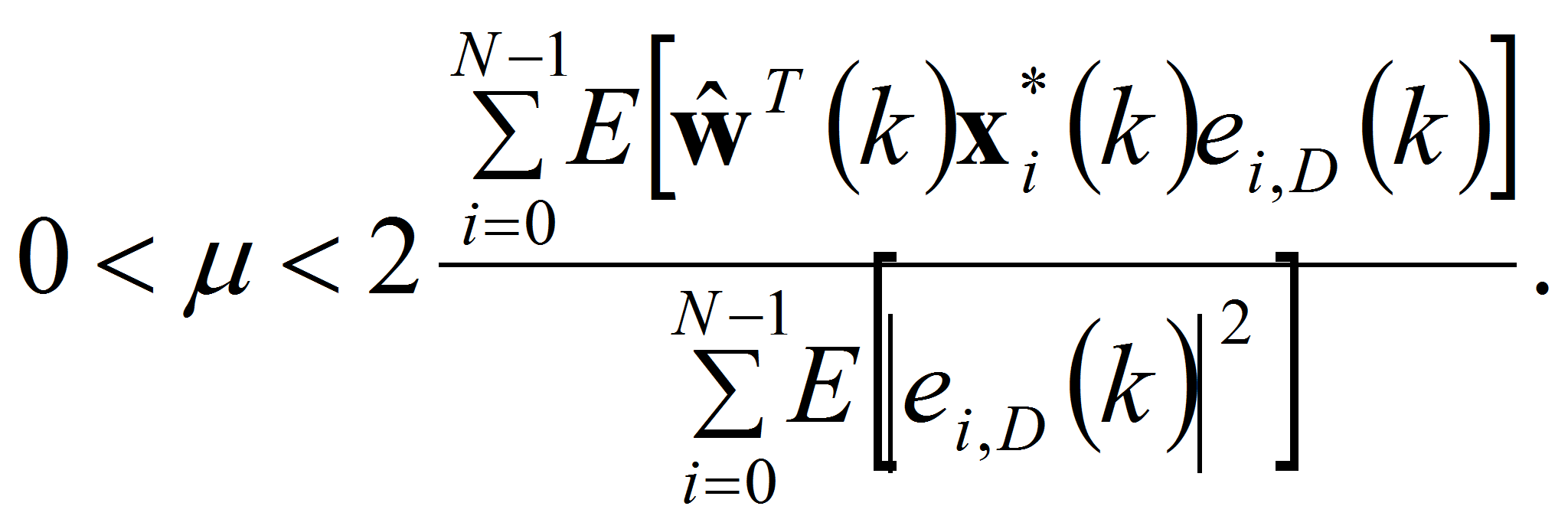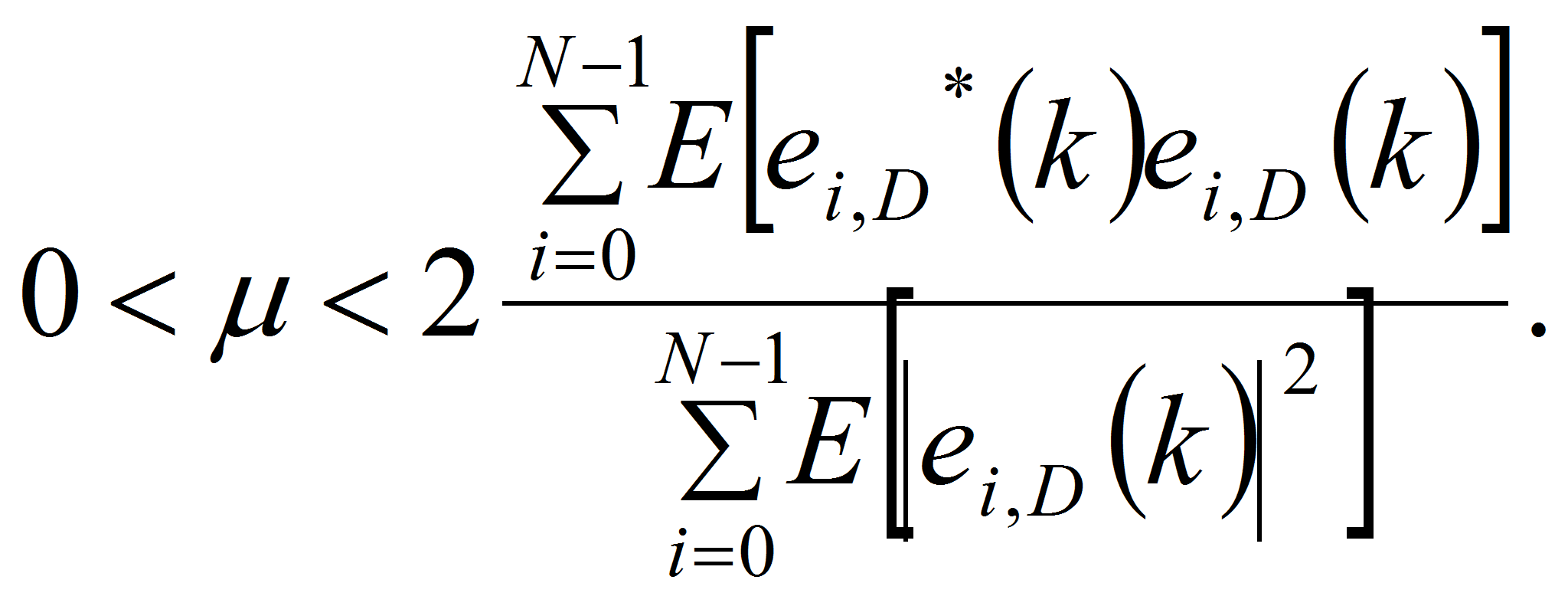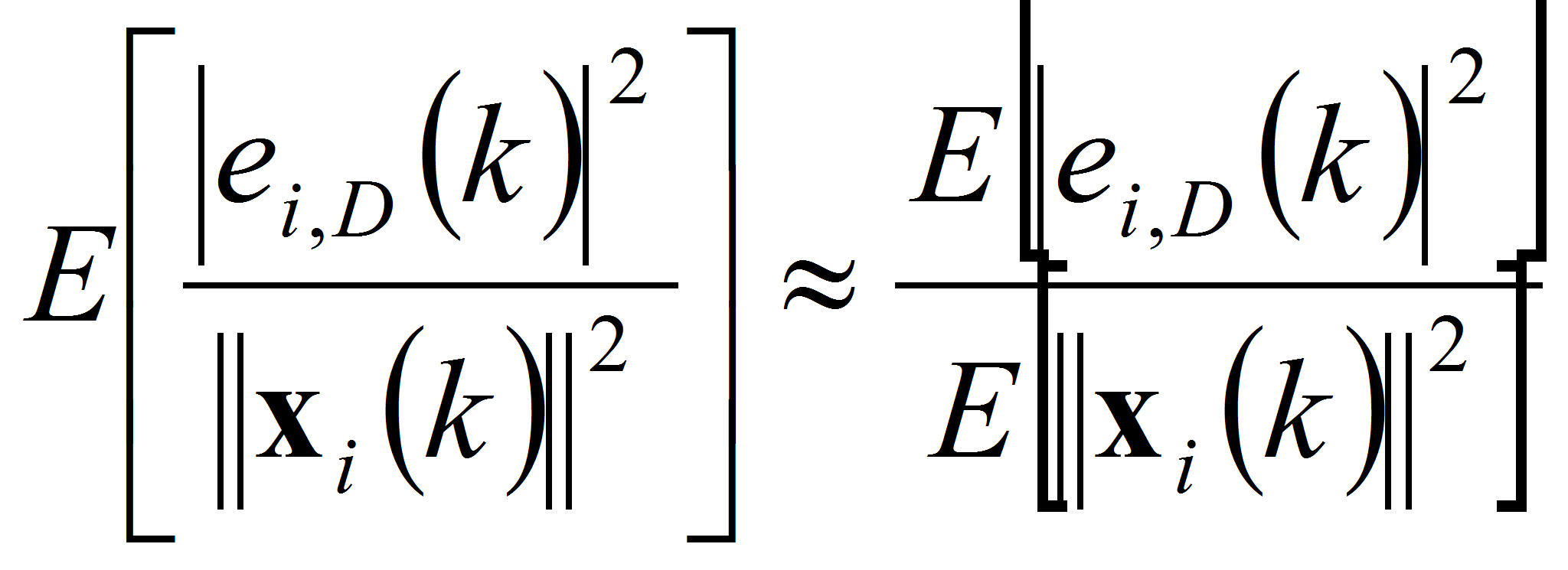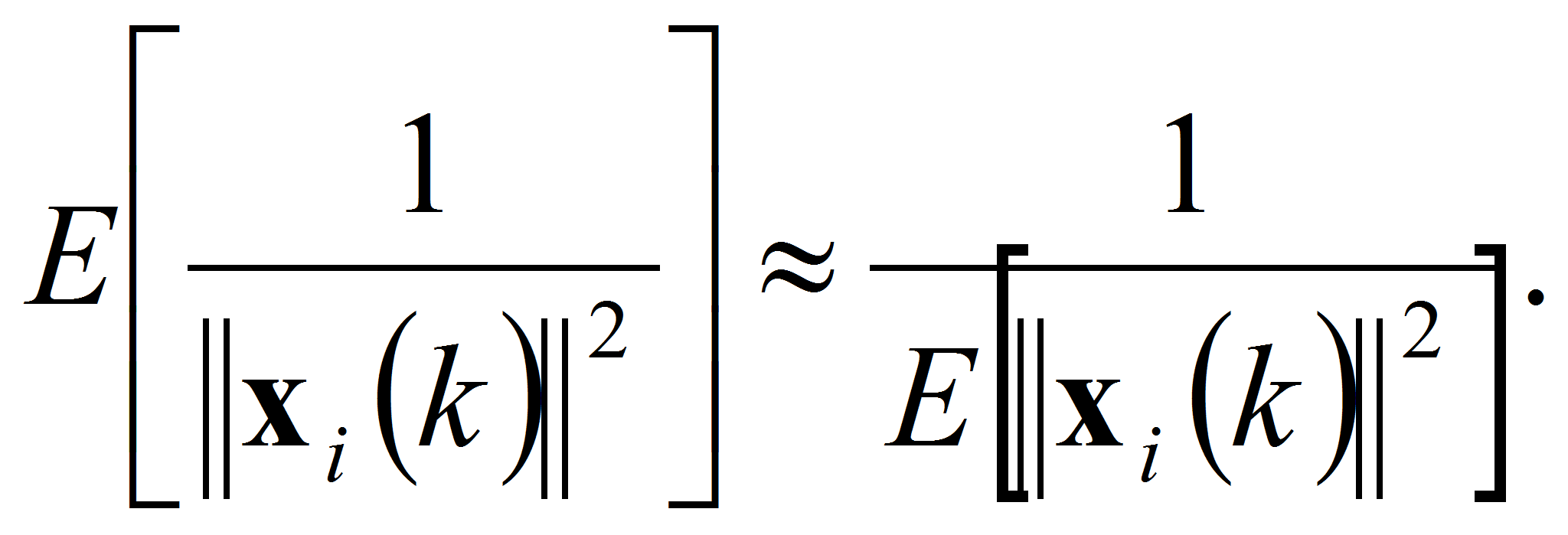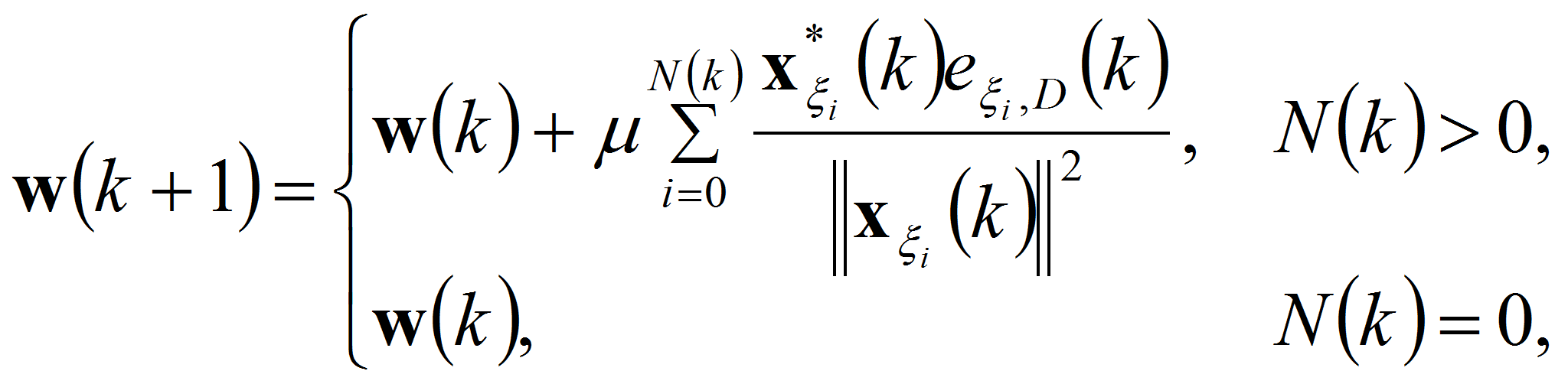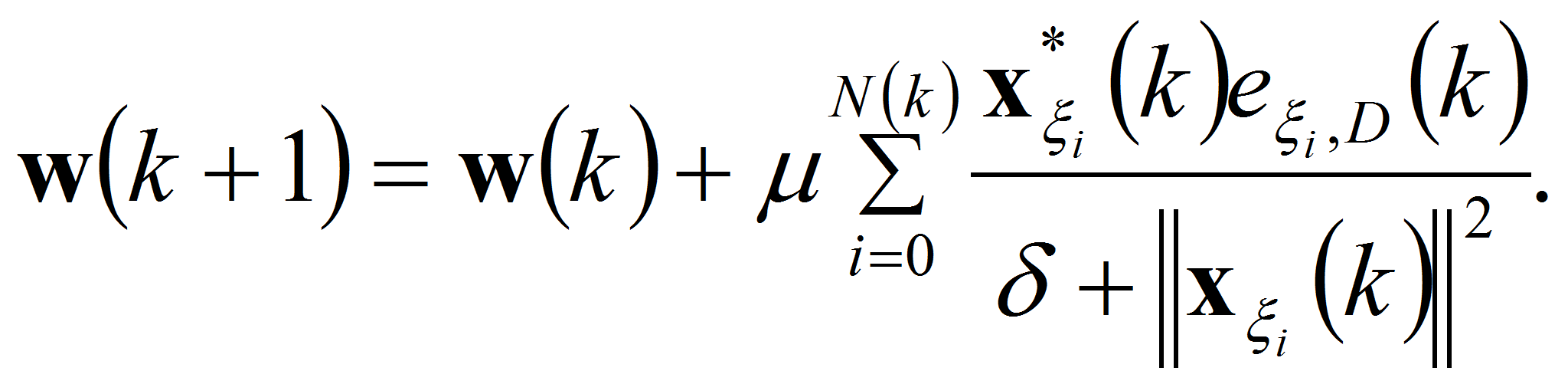Эквалайзер с настраиваемой структурой
Автор: Линович Александр Юрьевич
Рубрика: 2. Электроника, радиотехника и связь
Опубликовано в
международная научная конференция «Технические науки: традиции и инновации» (Челябинск, январь 2012)
Статья просмотрена: 947 раз
Библиографическое описание:
Линович, А. Ю. Эквалайзер с настраиваемой структурой / А. Ю. Линович. — Текст : непосредственный // Технические науки: традиции и инновации : материалы I Междунар. науч. конф. (г. Челябинск, январь 2012 г.). — Челябинск : Два комсомольца, 2012. — С. 20-29. — URL: https://moluch.ru/conf/tech/archive/6/1589/ (дата обращения: 24.04.2025).
- 1. Введение
Наиболее известным подходом к решению задачи оценивания неизвестных параметров канала связи является метод наименьших квадратов (МНК). С целью сокращения вычислительных затрат часто предпочитают использовать более простые градиентные алгоритмы, такие как хорошо известный алгоритм НСКО. Главным недостатком НСКО является медленная скорость настройки. Этот недостаток становится особенно важным в тех случаях, когда отсчёты входного сигнала оказываются сильно коррелированными между собой, а также в присутствии аддитивной помехи с неравномерно распределённой спектральной плотностью мощности.
Одно из направлений решения указанных выше проблем связано с построением многоканальных адаптивных фильтров (МАФ), в которых каждый канал работает только с некоторой предоставленной ему частью спектра, вычлененной посредством подсистемы фильтров анализа из широкополосного входного сигнала. Преимущество такого субполосного подхода связано с декорреляцией обрабатываемого сигнала при разбиении его на узкополосные составляющие. Поэтому переход к многоканальной структуре адаптивного фильтра, с одной стороны, обеспечивает более высокую скорость настройки эквалайзера, но, с другой стороны, требует введения в структуру эквалайзера подсистем анализа и синтеза для разбиения широкополосного входного сигнала на компоненты и последующего объединения полученных в процессе адаптивной обработки компонентов выходного сигнала в результирующий широкополосный выходной сигнал.
В настоящей работе рассмотрен МАФ, отличающийся от классических структур наличием единого вектора весовых коэффициентов для всех каналов. При этом фильтрация входного сигнала может выполняться двумя способами, о которых говорится в теоретической части статьи. Результаты проведённого компьютерного моделирования подтверждают, что использование методов самоорганизации в алгоритмах настройки МАФ позволяет значительно снизить вычислительные затраты на их реализацию и создаёт возможность повышения эффективности работы эквалайзеров при ограничениях, накладываемых производительностью выбранной элементной базы.
В статье предложены структура и алгоритм настройки многоканального эквалайзера с адаптивной структурой системы анализа-синтеза и проведён подробный анализ его работы. Описаны правила построения и настройки данного эквалайзера. Выведены расчётные соотношения для определения объёма вычислительных затрат.
2. Теоретическая часть
В современных системах широкополосной цифровой связи одной из важнейших проблем является необходимость обработки значительных объёмов данных в реальном масштабе времени. При имеющихся ограничениях, накладываемых доступной элементной базой, разработчики систем передачи данных стремятся разными способами снизить вычислительные затраты.
Одним из наиболее распространённых подходов к оценке оптимальных параметров адаптивного фильтра в настоящее время является метод наименьших квадратов (МНК). Его особенность прежде всего проявляется в отсутствии каких-либо жёстких претензий к априорной информации об оцениваемых параметрах и экспериментальных ошибках, что очень важно для задач, которые не допускают экспериментального повторения и в этом смысле являются однократными. При организации вычислительного процесса в реальном времени применяют рекуррентный алгоритм МНК [1, 2]. Однако при высокой частоте дискретизации обрабатываемого сигнала реализация рекуррентного алгоритма МНК в его традиционной форме является очень трудоёмкой в вычислительном плане задачей.
Поиск упрощений алгоритма МНК ведётся в основном по трём направлениям. Первое направление связано с упрощением процедуры обновления матрицы или полным отказом от неё. Здесь следует упомянуть известный алгоритм МНК с нормированием мощности входного сигнала (НМНК) [3 – 5]. Второе направление представлено эквалайзерами с обратной связью по решению, в которых задача обратного моделирования заменяется задачей прямого моделирования [6, 7]. Третье направление связано с переносом обработки сигнала в частотную область и активно использует быстрое преобразование Фурье или его модификации [4, 5]. Эквалайзеры на основе многоканальных адаптивных фильтров (МАФ), в которых каждый канал выполняет обработку входного сигнала в отдельной ограниченной полосе частот, часто относят к третьей из указанных выше групп эквалайзеров [8].
Классические МАФ, в каналах которых применяется алгоритм НМНК, подробно рассмотрены в [8, 9]. МАФ данного типа отличаются значительной экономией вычислительных затрат и одновременным улучшением качественных показателей процесса настройки. Сокращение объёма вычислительных затрат достигается благодаря использованию многоскоростной обработки сигналов. Ускорение и повышение точности настройки связаны с декорреляцией сигнала при разбиении на отдельные частотные компоненты и независимой адаптацией в каналах МАФ.
В настоящей работе рассмотрен МАФ, отличающийся от классических структур наличием единого вектора весовых коэффициентов для всех каналов. При этом фильтрация входного сигнала может выполняться двумя способами. В первом случае свёртка вектора отсчётов входной последовательности с вектором весовых коэффициентов адаптивного фильтра осуществляется в отдельных каналах структуры МАФ, работающих на пониженной частоте дискретизации, с последующим объединением компонентов с помощью подсистемы синтеза в результирующий выходной сигнал. Во втором случае выходная последовательность формируется на исходной частоте дискретизации, а настройка весовых коэффициентов выполняется на пониженной частоте: такой подход позволяет, с одной стороны, полностью исключить подсистему синтеза из структуры МАФ, а с другой стороны, избежать временной задержки, связанной с обработкой полезного сигнала системой анализа-синтеза. Экономия вычислительных затрат в таких МАФ может достигаться только за счёт динамического исключения каналов по указанному ниже критерию. Улучшение качественных показателей связано, как и для упомянутых выше классических МАФ, с декорреляцией. МАФ с похожими структурой и алгоритмом настройки были рассмотрены в [10, 11], но использовались они для подавления акустического эха и имели вещественные коэффициенты.
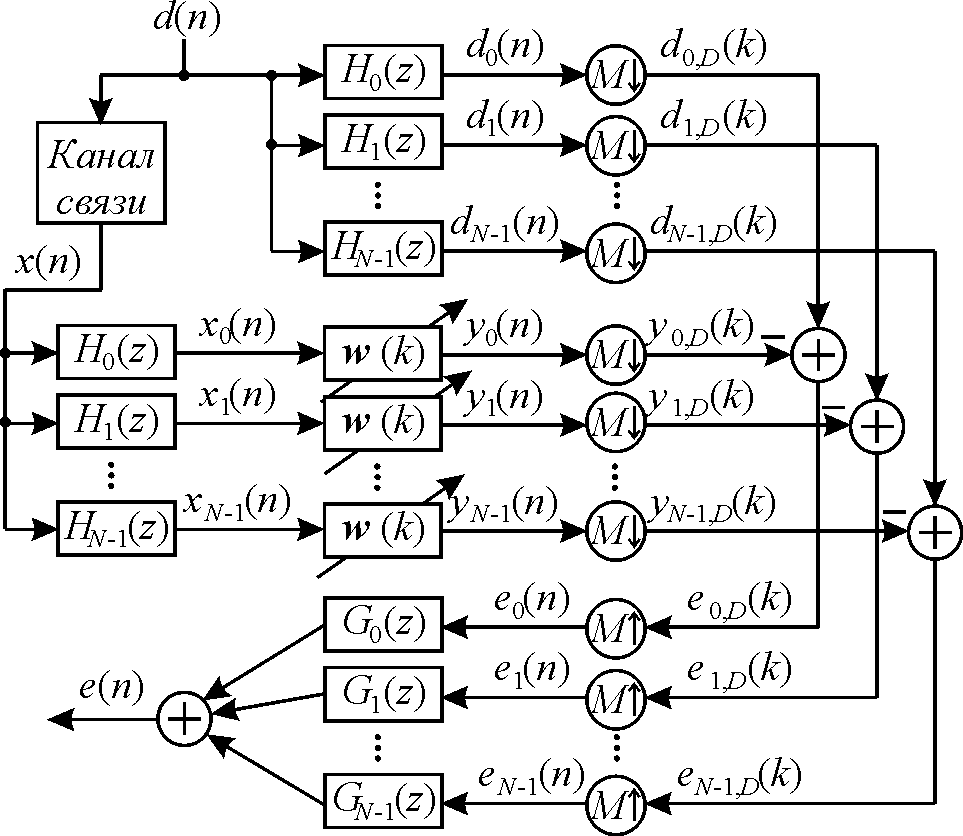
Теоретические исследования. Предлагаемая структура в общем виде показана на рисунке 1. Процесс формирования выходной последовательности y(n) на схеме не раскрыт, так как возможны два способа её формирования, о которых речь пойдёт ниже.
Рисунок 1 – Структурная схема МАФ
Предполагается, что на этапе настройки эквалайзера обучающий сигнал d(n) известен на приёмной стороне и отличается от переданного обучающего сигнала только задержкой. Эквалайзер должен настроить вектор весовых коэффициентов w(k) адаптивного КИХ-фильтра порядка L таким образом, чтобы минимизировать средний квадрат ошибки e(n) = d(n) – y(n), где y(n) – выходной сигнал эквалайзера. Если массив отсчётов, содержащихся в линии задержки адаптивного фильтра в момент времени n, обозначить как
то
или при переходе к многоканальной структуре и учёте операции децимации (обрабатывается только каждый M-й отсчёт)
где i – порядковый номер канала МАФ, k –индекс времени при обработке на пониженной частоте дискретизации.
Теперь получим правило обновления вектора весовых коэффициентов w(k). Критерием качества настройки эквалайзера целесообразно выбрать квадрат евклидовой нормы изменения вектора весовых коэффициентов, как это сделано, например, в [10]:
Аналогично [10], вводим N ограничений:
Методы решения задачи нахождения условного минимума (или максимума) функции нескольких переменных при наличии уравнений связи описаны во многих учебниках по высшей математике [12 – 15]. Тем не менее, в отличие от [10], в нашем случае сложность применения этих методов связана с необходимостью поиска минимума функции (1) комплексного аргумента. Не трудно проверить, что (1) не является аналитической функцией и для неё понятие производной не применимо.
Поэтому для того чтобы воспользоваться в дальнейшем методом неопределённых множителей Лагранжа, введём следующие обозначения:
где Re{} и Im{} — условные обозначения операций взятия вещественной и мнимой частей комплексной величины.
Введём 2N неопределённых вещественных коэффициентов (множителей Лагранжа), и на основе выражений (1) и (2) составим функцию
Следует заметить, что данная функция является квадратичной. Для нахождения точки минимума достаточно вычислить первую производную по w(k+1), приравнять её к нулевому вектору и решить полученное уравнение.
Вычислив первую производную (3) по w(k+1) и приравняв её к нулевому вектору, получим следующее векторное уравнение первого порядка:
Прежде, чем приступить к решению данного уравнения, упростим его.
Введём N новых переменных
![]() следующим образом:
следующим образом:
где j – мнимая единица. С учётом введённых выше обозначений, получим комплексное уравнение:
Поскольку сигнал ошибки в i-м канале определяется как
то с учётом (2) и (4) можно записать выражения для сигналов ошибки:
а упростив его, получить
где i принимает значения от 0 до N–1. Символ H обозначает операцию комплексно-сопряжённого транспонирования матрицы или вектора.
Введём новые обозначения:
Тогда система уравнений (5) запишется в матричном виде:
откуда
В [10] показано, что при незначительном перекрытии спектров соседних
каналов взаимной корреляцией можно пренебречь и считать матрицу
![]() диагональной матрицей. Тогда выражение (6) можно упростить:
диагональной матрицей. Тогда выражение (6) можно упростить:
С учётом (4) получаем правило обновления вектора весовых коэффициентов предлагаемого МАФ:
Получившееся соотношение напоминает по форме правило обновления весовых коэффициентов комплексного алгоритма НМНК [3 – 5]. Параметр μ представляет собой шаг адаптации алгоритма. Чем меньше μ, тем точнее выполняется настройка, но тем дольше продолжается переходной процесс.
Определим интервал значений параметра μ, при
которых предлагаемый алгоритм проявляет устойчивую сходимость. Пусть
![]() – вектор весовых коэффициентов, соответствующий оптимальной
настройке адаптивного КИХ-фильтра. И пусть
– вектор весовых коэффициентов, соответствующий оптимальной
настройке адаптивного КИХ-фильтра. И пусть
![]() – вектор невязки в определении весовых коэффициентов на k-й
итерации. Тогда устойчивая сходимость алгоритма
может быть выведена из условия [10]:
– вектор невязки в определении весовых коэффициентов на k-й
итерации. Тогда устойчивая сходимость алгоритма
может быть выведена из условия [10]:
Воспользовавшись (7) и предполагая независимость процессов настройки в соседних каналах, как это было сделано ранее, получим
где для упрощения записи символом Δ обозначено выражение:
Подставляя полученный результат в соотношение (8), запишем
Следовательно, параметр μ должен выбираться из условия:
Если аддитивный шум, вносимый каналом связи, достаточно мал, что им можно пренебречь, по сравнению с шумом адаптивного процесса, возникающим в результате постоянной подстройки его весовых коэффициентов при выбранном шаге адаптации μ, то
и
Упрощая последнее неравенство, окончательно получим
В завершение теоретического раздела статьи,
выведем правило исключения каналов МАФ. Из (8) и дальнейших
рассуждений следует, что алгоритм сходится, если при переходе к
очередной итерации алгоритма убывает
средний квадрат невязки, то есть если Δ > 0. Причём
увеличение Δ, приводит к ускорению процесса настройки
алгоритма. Однако если раньше мы предположили, что аддитивный
шум достаточно мал и пренебрегли его величиной, то теперь учтём
дисперсию шума, обозначив её
![]() ,
где
,
где
![]() – составляющая шума, попадающая в i-й
канал МАФ.
– составляющая шума, попадающая в i-й
канал МАФ.
С учётом того, что
выражение (9) примет следующий вид:
При этом предполагается, что составляющие
аддитивного шума канала связи, поступающие в разные каналы МАФ, не
зависят друг от друга и подчиняются гауссовскому закону
распределения. Кроме того, аддитивный шум, вносимый каналом
связи, считается независимым от передаваемого полезного сигнала x(n),
а невязка
![]() считается независимой от величины аддитивного шума на предыдущей
итерации (то есть, от
считается независимой от величины аддитивного шума на предыдущей
итерации (то есть, от
![]() ,
где
,
где
![]() – порядковый номер канала МАФ).
– порядковый номер канала МАФ).
В [16] показано, что разброс значений
![]() ,
проявляющийся в процессе настройки адаптивного фильтра высокого
порядка, на интервале нескольких последовательно взятых итераций в
большинстве практических приложений оказывается настолько мал, что им
можно пренебречь. Поэтому, следуя рассуждениям [16], будем считать,
что
,
проявляющийся в процессе настройки адаптивного фильтра высокого
порядка, на интервале нескольких последовательно взятых итераций в
большинстве практических приложений оказывается настолько мал, что им
можно пренебречь. Поэтому, следуя рассуждениям [16], будем считать,
что
и
Тогда выражение Δ, записанное ранее в форме (11), можно заменить его приближённой оценкой:
При выполнении (10) постоянный коэффициент
![]() всегда оказывается положительным. И как следует из (12), при
выполнении условия
всегда оказывается положительным. И как следует из (12), при
выполнении условия
![]() i-й канал МАФ способствует увеличению
величины
i-й канал МАФ способствует увеличению
величины
![]() ,
а при выполнении обратного ему условия
,
а при выполнении обратного ему условия
![]() i-й канал МАФ способствует уменьшению
величины
i-й канал МАФ способствует уменьшению
величины
![]() .
Поэтому с целью ускорения процесса настройки адаптивного фильтра
имеет смысл отключать каналы, влияние которых на k-й
итерации не приводит к уменьшению среднего квадрата невязки
.
Поэтому с целью ускорения процесса настройки адаптивного фильтра
имеет смысл отключать каналы, влияние которых на k-й
итерации не приводит к уменьшению среднего квадрата невязки
![]() ,
проводя настройку только в тех каналах структуры МАФ, для которых
выполняется условие
,
проводя настройку только в тех каналах структуры МАФ, для которых
выполняется условие
Поскольку величину математического ожидания невозможно определить по результату одного отдельного измерения, то в последнем неравенстве приходится ввести замену:
Величина аддитивного шума на выходе канала связи в большинстве практических приложений оценивается на интервале специально выделенных пауз, когда передача полезных сигналов прекращается, или в рабочем режиме на основе какой-либо из множества широко известных специальных методик.
Введём несколько обозначений. Пусть на k-й
итерации выбрано
![]() каналов МАФ. Обозначим всё множество выбранных каналов
каналов МАФ. Обозначим всё множество выбранных каналов
Элементами
![]() данного множества являются порядковые номера выбранных каналов МАФ на
k-й итерации.
данного множества являются порядковые номера выбранных каналов МАФ на
k-й итерации.
Теперь с учётом введённых обозначений предлагаемый алгоритм настройки вектора весовых коэффициентов комплексного эквалайзера с адаптивной системой анализа-синтеза запишется в следующей аналитической форме:
где
![]() – множество каналов МАФ, для которых выполняется неравенство
– множество каналов МАФ, для которых выполняется неравенство
На основе описанных выше теоретических исследований разработаны два алгоритма настройки эквалайзера (таблицы 1 и 2).
В таблицах 1 и 2 используются следующие обозначения. N
– число каналов МАФ, L – число
настраиваемых весовых коэффициентов (порядок МАФ), LH
– порядок фильтров подсистемы анализа, LG
– порядок фильтров подсистемы синтеза, M
– коэффициент децимации, N(k)
– число каналов, для которых проводится настройка МАФ.
![]() – объём вычислительных затрат, определяемый как среднее число
операций комплексного умножения, выполняемых за время Ts,
равное шагу дискретизации входного сигнала МАФ.
– объём вычислительных затрат, определяемый как среднее число
операций комплексного умножения, выполняемых за время Ts,
равное шагу дискретизации входного сигнала МАФ.
Малая положительная константа δ вводится для того, чтобы повысить устойчивость алгоритма в случае приёма сигнала малой мощности [1, 2, 10].
Несмотря на то, что система анализа-синтеза функционирует на частоте дискретизации входного сигнала, затраты на её реализацию удаётся сократить в M раз. Сокращение вычислительных затрат на обработку сигналов в системе анализа-синтеза достигается переходом к полифазной структуре, которая подробно рассмотрена в таких фундаментальных работах по теории многоскоростной обработки сигналов как [17 – 19]. Если входной сигнал является вещественным, то половину каналов МАФ можно исключить из рассмотрения, поскольку спектр вещественного сигнала симметричен относительно нулевой частоты (или относительно половины частоты дискретизации).
Таблица 1
Алгоритм МАФ, использующий подсистему синтеза (далее МАФ-1)
|
Выполняемые действия |
|
|
Операции, выполняемые для отсчётов n = 0, 1, 2, … на частоте дискретизации 1/Ts |
|
|
1) Разделение входного и обучающего сигналов на компоненты подсистемой анализа: |
|
|
2) Объединение компонентов выходного сигнала подсистемой синтеза: |
|
|
Операции, выполняемые для отсчётов k = 0, 1, 2, … на частоте дискретизации 1/(MTs) |
|
|
1) Вычисление компонентов выходного сигнала и оценка сигналов ошибки: |
|
|
|
|
3. Экспериментальные исследования
Для эксперимента была выбрана модель, аналогичная предложенной в [20]: 4-позиционная относительная фазовая манипуляция (QPSK) с использованием кода Грея, скорость передачи равна 10 Мбит/с. Фильтрация импульсов осуществляется на приёмной и передающей сторонах цифровым фильтром с характеристикой типа «приподнятый косинус», нормированной на квадратный корень, и коэффициентом спада, равным 0,23. Как и в [20] при модуляции используется одна несущая частота, но обработка сигнала выполняется без перехода в частотную область при помощи алгоритма быстрого преобразования Фурье. Кроме того, предполагается, что настройка происходит по известному в приёмнике эталонному сигналу, поэтому пилот-сигналы в модели отсутствуют.
Таблица 2
Алгоритм МАФ, не использующий подсистему синтеза (далее МАФ-2)
|
Выполняемые действия |
|
|
Операции, выполняемые для отсчётов n = 0, 1, 2, … на частоте дискретизации 1/Ts |
|
|
1) Вычисление очередного отсчёта выходного сигнала: |
|
|
L |
|
|
2) Разделение входного и обучающего сигналов на компоненты подсистемой анализа: |
|
|
Операции, выполняемые для отсчётов k = 0, 1, 2, … на частоте дискретизации 1/(MTs) |
|
|
1) Оценка сигналов ошибки: |
|
|
|
|
В качестве модели канала связи выбран стационарный канал с многолучевым распространением сигнала в среде городского типа [20, 21]. Параметры такого канала приводятся ниже в табличной форме (таблица 3).
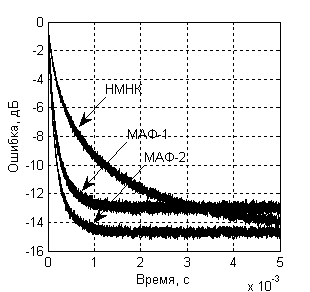
Сравнить результаты настройки эквалайзеров 512-го порядка на основе адаптивных алгоритмов МАФ-1 и МАФ-2 с известным алгоритмом НМНК позволяет рисунок 2.
Таблица 3
Параметры канала связи
|
Номер луча |
Задержка луча, мкс |
Мощность луча, дБ |
|
1 |
0 |
3,00 |
|
2 |
0,010 |
5,22 |
|
3 |
0,030 |
6,98 |
|
4 |
0,360 |
5,22 |
|
5 |
0,370 |
7,44 |
|
6 |
0,385 |
9,19 |
|
7 |
0,250 |
4,72 |
|
8 |
0,260 |
6,94 |
|
9 |
0,280 |
8,69 |
|
10 |
1,040 |
8,19 |
|
11 |
1,045 |
10,41 |
|
12 |
1,065 |
12,17 |
|
13 |
2,730 |
12,05 |
|
14 |
2,740 |
14,27 |
|
15 |
2,760 |
16,03 |
|
16 |
4,600 |
15,50 |
|
17 |
4,610 |
17,72 |
|
18 |
4,625 |
19,48 |
Рисунок 2 – Обучающие
кривые для эквалайзеров на основе алгоритмов
МАФ-1, МАФ-2 и НМНК
При моделировании на выходе канала связи к полезному сигналу добавлялся аддитивный белый гауссовский шум. Отношение сигнал-шум было выбрано равным 18 дБ. В результате число каналов N(k) спадало в среднем до 7 – 8 в установившемся режиме (рисунок 3).
Рисунок 3 – Среднее число каналов, для которых проводится настройка МАФ
Судя по рисунку 2, при заданном порядке адаптивного фильтра многоканальный эквалайзер настраивается значительно быстрее, что объясняется декорреляцией входного сигнала при разбиении его на отдельные полосы частот подсистемой анализа. Кроме того, эквалайзер на основе алгоритма МАФ-2, не использующий подсистему синтеза, настраивается заметно быстрее и точнее своего аналога – эквалайзера на основе алгоритма МАФ-1. По точности настройки в установившемся режиме эквалайзер на основе алгоритма МАФ-2 ничем не уступает эквалайзеру на основе известного алгоритма НМНК, если не учитывать предела точности МАФ-2, определяемого ошибкой восстановления сигнала системой анализа-синтеза. В проведённых экспериментах система анализа-синтеза строилась по методике, предложенной в [22]. Порядок фильтра-прототипа был задан равным 80.
При проведении компьютерного моделирования были выбраны следующие численные значения для перечисленных выше параметров. Использовался 16-канальный комплексный адаптивный фильтр (N = 16) с 14-кратным понижением частоты дискретизации (M = 14). Порядки фильтров анализа и синтеза были выбраны одинаковыми LH = LG = 80, порядки всех адаптивных фильтров L были равны 512.
Не трудно оценить затраты на реализацию адаптивных
алгоритмов. Эквалайзер на основе алгоритма МАФ-1 требует
![]() = 2048 + 73∙N(k)
< 2121 умножений на отсчёт, алгоритм МАФ-2 требует
= 2048 + 73∙N(k)
< 2121 умножений на отсчёт, алгоритм МАФ-2 требует
![]() = 2469 + 73∙N(k)
< 2542 умножений на отсчёт. Учитывая, что в
установившемся режиме (рисунок 3) число используемых каналов N(k)
спадает в среднем до 7 – 8, вычислительные затраты на
реализацию МАФ можно оценить следующим образом: эквалайзер на основе
алгоритма МАФ-1 требует в среднем 2080 умножений на отсчёт,
эквалайзер на основе алгоритма МАФ-2 требует в среднем 2500 умножений
на отсчёт. Для сравнения, при использовании стандартного алгоритма
НМНК необходимо 3∙512 = 1536 умножений.
= 2469 + 73∙N(k)
< 2542 умножений на отсчёт. Учитывая, что в
установившемся режиме (рисунок 3) число используемых каналов N(k)
спадает в среднем до 7 – 8, вычислительные затраты на
реализацию МАФ можно оценить следующим образом: эквалайзер на основе
алгоритма МАФ-1 требует в среднем 2080 умножений на отсчёт,
эквалайзер на основе алгоритма МАФ-2 требует в среднем 2500 умножений
на отсчёт. Для сравнения, при использовании стандартного алгоритма
НМНК необходимо 3∙512 = 1536 умножений.
Таким образом, алгоритм МАФ-2 позволяет существенно повысить скорость настройки эквалайзер по сравнению со стандартным алгоритмом НМНК при той же точности и сравнимых вычислительных затратах. Алгоритм МАФ-1 несколько уступает в точности, но превосходит МАФ-2 по экономии вычислительных затрат.
Заключение. В статье предложены структура и алгоритм настройки многоканального эквалайзера с адаптивной структурой системы анализа-синтеза и проведён подробный анализ его работы. Описаны правила построения и настройки данного эквалайзера. Выведены расчётные соотношения для определения объёма вычислительных затрат.
- Литература:
1. Чураков Е.П. Математические методы обработки экспериментальных данных в экономике: Учеб. пособие. – М.: Финансы и статистика, 2004. – 240 с.
2. Певзнер Л.Д., Чураков Е.П. Математические основы теории систем: Учеб. пособие. – М.: Высш. шк., 2009. – 503 с.
3. Уидроу Б. и др. Комплексная форма алгоритма НСКО // ТИИЭР. 1975. – № 3. – С. 49 – 51.
4. Уидроу Б., Стирнз С. Адаптивная обработка сигналов / Пер с англ. – М.: Радио и связь, 1989. – 440 с.
5. Коуэн К.Ф., Грант П.М. Адаптивные фильтры / Пер. с англ. – М.: Мир, 1988. – 392 с.
6. Прокис Д. Цифровая связь / Пер. с англ. – М.: Радио и связь, 2000. – 800 с.
7. Скляр Б. Цифровая связь. Теоретические основы и практическое применение. Пер. с англ. 2-е изд. – М.: Вильямс, 2003. – 1104 с.
8. Haykin S., Adaptive filter theory, 4th ed. – NJ: Prentice-Hall, 2001. – 936 с.
9. Линович А.Ю. Применение методов частотно-временной декомпозиции при решении задачи обратного моделирования // Цифровая обработка сигналов. 2005. – № 3. – С. 28 – 37.
10. Lee K.A., Gan W.S. Improving convergence of the NLMS algorithm using constrained subband updates // IEEE signal processing letters. 2004. – № 9. – C. 736 – 739.
11. Kim S.E., Choi Y.S., Song M.K., Song W.J. A subband adaptive filtering algorithm employing dynamic selection of subband filters // IEEE signal processing letters. 2010. – № 3. – C. 245 – 248.
12. Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. – М.: Физматгиз, 1963. – 856 с.
13. Акулич И.Л. Математическое программирование в примерах и задачах: Учеб. пособие. — М.: Высш. шк., 1986. — 319 с.
14. Пантелеев А.В., Летова Т.А. Методы оптимизации в примерах и задачах: Учеб. пособие. — М.: Высш. шк., 2002. — 544 с.
15. Зорич В.А. Математический анализ. Часть I. 3-е изд., испр. и доп. — М.: МЦНМО, 2001. — XVI + 664 с.
16. Tandon A., Swamy M.N.S., Ahmad M.O. Partial-update L∞-norm based algorithms // IEEE transactions on circuits and systems I. 2007. – № 2. – C. 411 – 419.
17. Crochiere R.E., Rabiner L.R. Multirate digital signal processing. – NJ: Prentice-Hall, 1983. – 411 с.
18. Витязев В.В. Цифровая частотная селекция сигналов. – М.: Радио и связь, 1993. – 240 с.
19. Вайдьянатхан П.П. Цифровые фильтры, блоки фильтров и полифазные цепи с многочастотной дискретизацией: Методический обзор // ТИИЭР. 1990. – № 3. – С. 77–119.
20. Ng B., Lam C.T., Falconer D. Turbo frequency domain equalization for single-carrier broadband wireless systems // IEEE transactions on wireless communications. 2007 – № 2. – С. 759 – 767.
21. Auer G., et al. Assessment of radio-link technologies // WINNER Deliverable D2.3 (section 3.1). Feb. 2005. – Available: https://www.istwinner.org/Deliverable Documents/D2-3.pdf.
22. Harteneck M., Weiss S., Stewart R.W. Design of near perfect reconstruction oversampled filter banks for subband adaptive filters // IEEE transactions on circuits and systems II. 1999. – № 8. – С. 1081 – 1086.