Применение модели линейного предсказания для анализа стохастических сигналов
Автор: Кагановский Юрий Дмитриевич
Рубрика: 2. Электроника, радиотехника и связь
Опубликовано в
международная научная конференция «Технические науки: традиции и инновации» (Челябинск, январь 2012)
Статья просмотрена: 4139 раз
Библиографическое описание:
Кагановский, Ю. Д. Применение модели линейного предсказания для анализа стохастических сигналов / Ю. Д. Кагановский. — Текст : непосредственный // Технические науки: традиции и инновации : материалы I Междунар. науч. конф. (г. Челябинск, январь 2012 г.). — Челябинск : Два комсомольца, 2012. — С. 12-14. — URL: https://moluch.ru/conf/tech/archive/6/1596/ (дата обращения: 21.04.2025).
В начале нового тысячелетия в России начался активный переход на цифровые стандарты связи. Региональные и общегосударственные операторы отказываются от устаревшего аналогового оборудования АТС в пользу намного более производительного и компактного, цифрового. В это время для специалистов в области телекоммуникаций стоит первоочередная задача проектирования удобных, производительных и экономически выгодных систем связи. Ключевым моментом в реализации этой задачи является достижение как можно большего количества подключенных к сети абонентов при как можно меньшем количестве сложного оборудования и высоком качестве связи. Под качеством связи зачастую принято понимать качество речи, которую абонент слышит в трубке телефона. Для количественного описания процессов формирования и передачи речевых сигналов было предложено много различных моделей. Можно, однако, с уверенностью сказать, что ни одна из них не позволяет объяснить все характеристики человеческой речи. Такая модель, в силу своей большой сложности, вероятно, и не потребуется. Во всех практических случаях при выборе математической модели стремятся обеспечить ее минимальную сложность при максимальной точности. Одной из наиболее удачных моделей акустического речевого сигнала является линейная модель, разработанная Фантом. Эта модель далее будет называться моделью речеобразования.
В последние годы в задачах моделирования речевых сигналов широко применялись математические методы линейного предсказания. Модель на основе линейного предсказания может быть легко преобразована в модель речеобразования. Важным ее достоинством является относительная простота оценки параметров, использующей линейные процедуры обработки сигнала. На основе данной модели строятся LPC-вокодеры, или т.н. липредеры. В подобных вокодерах используются алгоритмы линейного предсказания, с помощью которых при анализе в передающем устройстве определяются коэффициенты предсказания, а в приемном устройстве на основе этих коэффициентов с помощью рекурсивного цифрового фильтра синтезируется эквивалент голосового тракта. Эти системы получили наибольшее распространение в мире и являются одними из самых перспективно развивающихся.
Основной проблемой, возникающей при анализе недетерминированных сигналов разнообразной природы (речевых, медицинских, сейсмических, геофизических при поиске и разработке месторождений полезных ископаемых) и динамических систем, является определение их временных и частотных характеристик, поскольку любой недетерминированный сигнал и динамическая система в принципе являются нелинейными объектами, что чрезвычайно усложняет их анализ.
Однако всегда можно выделить некоторый временной
интервал
![]() (Т– период
дискретизации), на котором параметры объекта изменяются не слишком
сильно. Такой интервал называют интервалом квазистационарности, а
параметры объекта на этом интервале считаются постоянными. Отрезок
сигнала x(nT)
на интервале
(Т– период
дискретизации), на котором параметры объекта изменяются не слишком
сильно. Такой интервал называют интервалом квазистационарности, а
параметры объекта на этом интервале считаются постоянными. Отрезок
сигнала x(nT)
на интервале
![]() называется кадром.
называется кадром.
Если построить достаточно точную параметрическую модель
объекта для интервала квазистационарности, то ее можно использовать в
самых различных случаях, в том числе, например, в системах управления
и сжатия данных. Самыми простыми являются линейные модели, которые
легко описываются в терминах передаточных функций [2, с. 125].
Наиболее полной в указанном смысле моделью представляется рекурсивная
система порядка К=М – 1,
описываемая передаточной функцией:
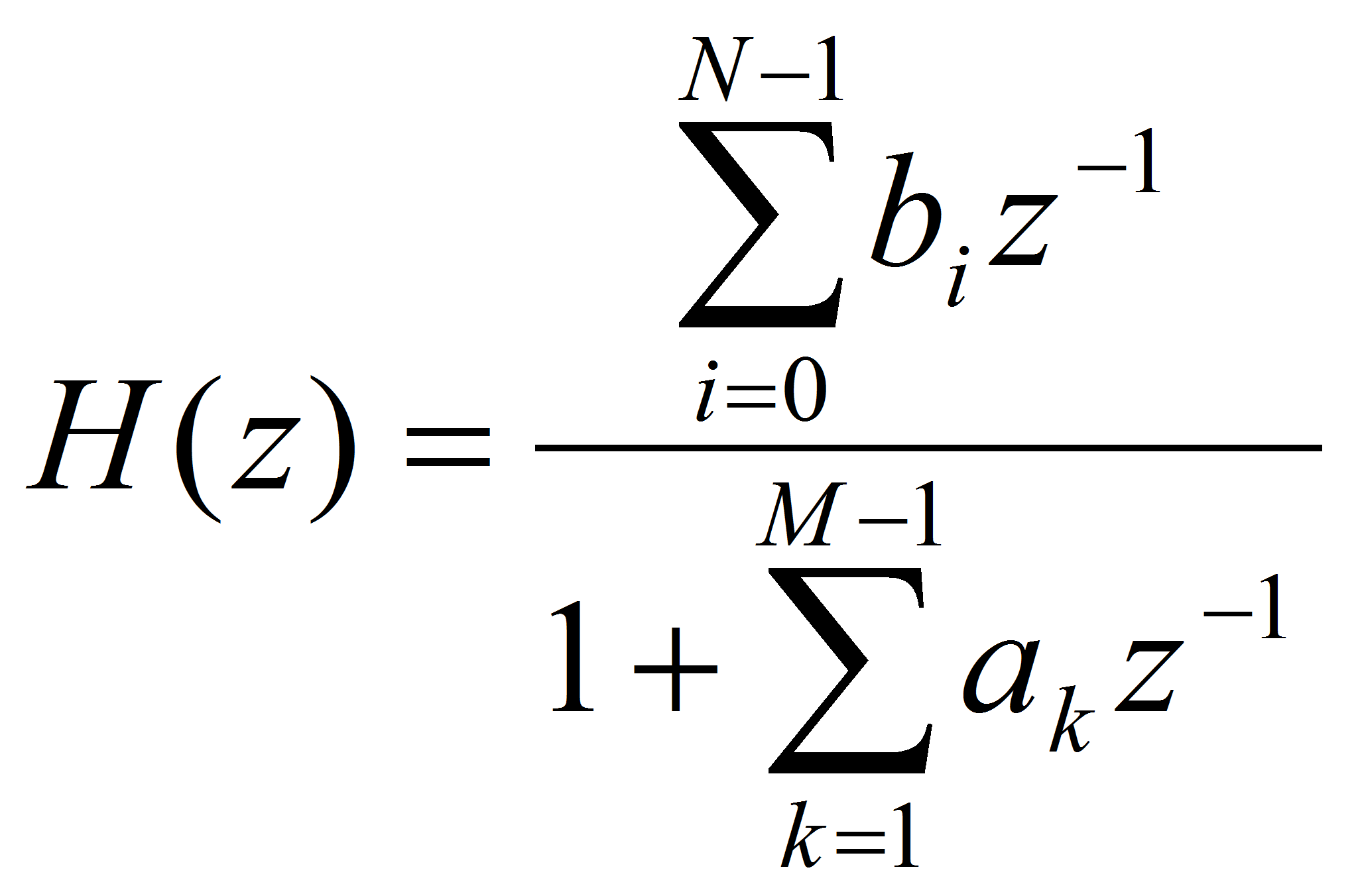 или соответствующим разностным уравнением:
или соответствующим разностным уравнением:
![]() .
.
Наиболее широко в настоящее время применяется полюсная модель, числитель передаточной функции (левая сумма в разностном уравнении) которой содержит только один коэффициент b0.
Пусть на некоторую линейную модель системы с
передаточной функцией H(z)
воздействует сигнал возбуждения x(n),
а на ее выходе формируется сигнал y(n).
Параметры системы, т.е. коэффициенты передаточной функции,
неизвестны. Требуется найти коэффициенты {ak},
такие, чтобы на интервале квазистационарности выполнялось равенство:
![]() при условии, что сигнал возбуждения x(n)
неизвестен. Фактически необходимо предсказать текущее значение
сигнала y(n)
по его известным предыдущим отсчетам. Таким образом, можно сделать
вывод, что линейное предсказание – это вычислительная
процедура, позволяющая по некоторой линейной комбинации L
предшествующих взвешенных отсчетов недетерминированного сигнала
предсказать (с определенной точностью) будущее значение отсчета.
при условии, что сигнал возбуждения x(n)
неизвестен. Фактически необходимо предсказать текущее значение
сигнала y(n)
по его известным предыдущим отсчетам. Таким образом, можно сделать
вывод, что линейное предсказание – это вычислительная
процедура, позволяющая по некоторой линейной комбинации L
предшествующих взвешенных отсчетов недетерминированного сигнала
предсказать (с определенной точностью) будущее значение отсчета.
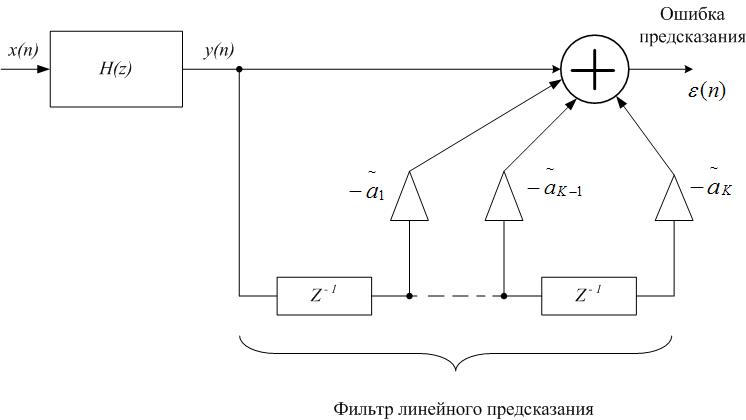
Рис. 1. Линейная модель системы
Практическая важность линейного предсказания состоит в оценке спектра исследуемого сигнала на его отрезке (кадре) длиной в L отсчетов, а с точки зрения фильтрации – в получении рекурсивного адаптивного фильтра порядка K=M – 1 на участке квазистационарности, т.е. на том временном отрезке длительностью LT (T – период дискретизации), где коэффициенты фильтра остаются постоянными. Итогом решения задачи линейного предсказания будет являться получение коэффициентов адаптивного фильтра, АЧХ которого с хорошей степенью приближения совпадает с формой спектра сигнала в кадре [3, с. 46].
-
Задача линейного предсказания сформулируем следующим
образом. На выходе некоторой системы наблюдается сигнал y(n);
известно, что эта система:
- 1. Полюсного типа с передаточной функцией вида:
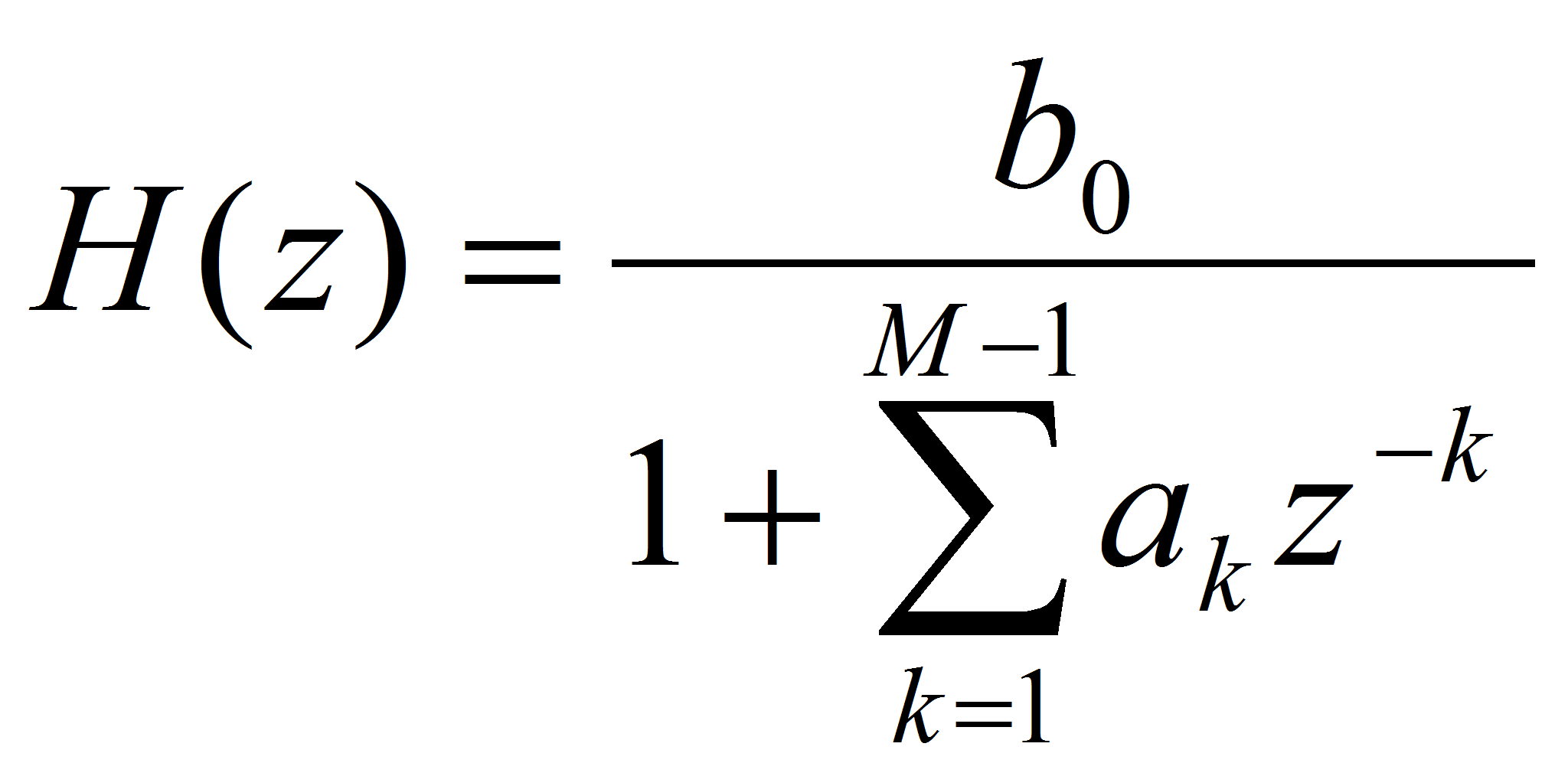 ,
,- 2. Имеет порядок K=M – 1,
- 3.Сигнал возбуждения не наблюдается.
- Требуется найти коэффициенты {ak}.
- Подход к решению поставленной задачи состоит в следующем.
- Согласно формуле передаточной функции, представленной выше, сигнал y(n) определяется выражением:
 .
.
- 1. Полюсного типа с передаточной функцией вида:
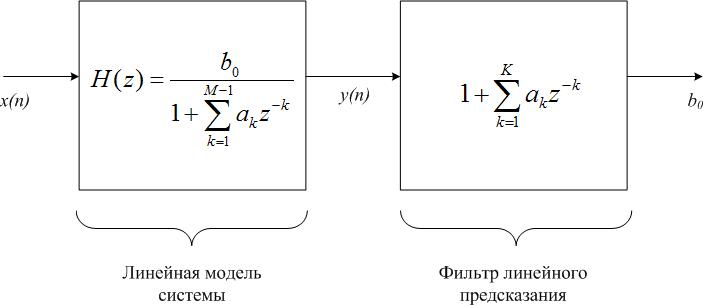
Рис. 2. Решение задачи линейного предсказания
-
- Включим последовательно с искомой системой КИХ-фильтр с передаточной функцией:
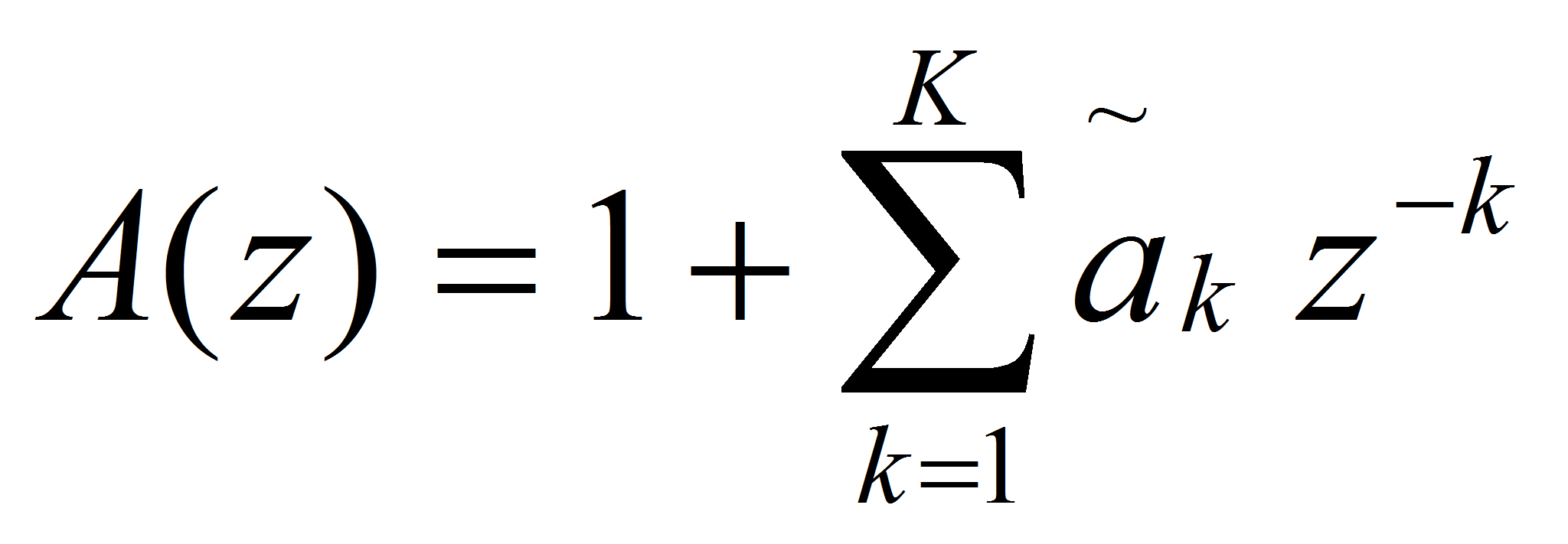 ,
коэффициенты которой
,
коэффициенты которой
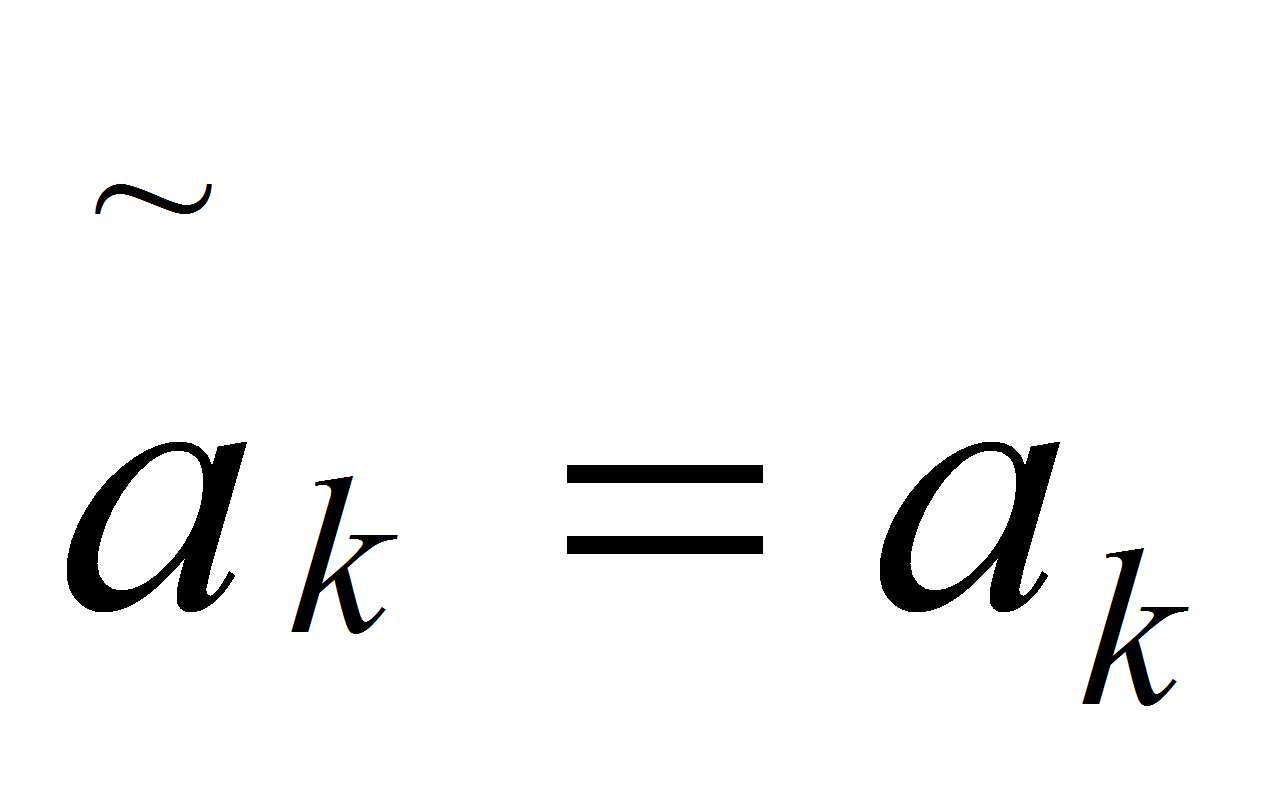 .
Передаточная функция образованной системы получит вид:
.
Передаточная функция образованной системы получит вид:
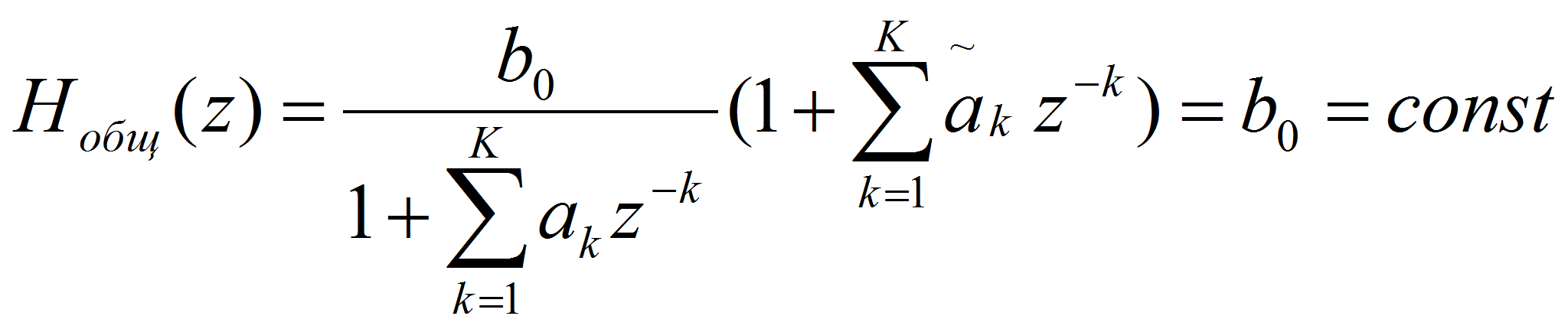 .
. - Включим последовательно с искомой системой КИХ-фильтр с передаточной функцией:
КИХ-фильтр с передаточной функцией A(z)
называется фильтром линейного предсказания, или
фильтром-предсказателем, его порядок K
– порядком предсказания, а его коэффициенты
![]() - коэффициентами линейного предсказания [1, с. 84].
- коэффициентами линейного предсказания [1, с. 84].
В действительности коэффициенты
![]() будут отличаться от точных значений ak,
поэтому предсказываемое значение сигнала
будут отличаться от точных значений ak,
поэтому предсказываемое значение сигнала
![]() будет отличаться от точного y(n)
на величину ошибки предсказания (при n
> 0):
будет отличаться от точного y(n)
на величину ошибки предсказания (при n
> 0):
![]() ,
которую называют остатком.
,
которую называют остатком.
Рис. 3. Структурная схема системы с фильтром-предсказателем
Схема решения задачи линейного
предсказания и формулы передаточной функции показывают, что
передаточная функция построенной системы с точностью до коэффициента
b0
представляет собой обратную передаточную функцию (а потому и
частотную характеристику) фильтра-предсказателя:
![]() ,
откуда видно, что линейное предсказание – это способ оценки
спектра сигнала на выходе линейного тракта с неизвестными
параметрами.
,
откуда видно, что линейное предсказание – это способ оценки
спектра сигнала на выходе линейного тракта с неизвестными
параметрами.
Таким образом, данный алгоритм применения линейного предсказания можно применять к различного рода недетерминированным сигналам, в том числе и к речевым, что открывает широкие возможности применения данного предсказания в области компрессии речевых данных.
Литература:
Рабинер Л., Гоулд Б., Теория и применение цифровой обработки сигналов / Пер.с англ.; Под ред. Ю.И. Александрова. – М.: Мир, 1978. – 848 с.
Сергиенко А.Б. Цифровая обработка сигналов. 2 – изд. – СПб.: Питер, 2006. – 608 с.
Феер К. Беспроводная цифровая связь. Методы модуляции и расширения спектра. Пер с англ. – М.: Радио и связь, 2000. – 253 c.