Оценка надежности трубопроводов, прокладываемых в промерзающих пучинистых грунтах
Авторы: Цапурин Константин Александрович, Скворцов Юрий Васильевич, Глушков Сергей Валериевич
Рубрика: 7. Машиностроение
Опубликовано в
международная научная конференция «Технические науки: теория и практика» (Чита, апрель 2012)
Статья просмотрена: 1801 раз
Библиографическое описание:
Цапурин, К. А. Оценка надежности трубопроводов, прокладываемых в промерзающих пучинистых грунтах / К. А. Цапурин, Ю. В. Скворцов, С. В. Глушков. — Текст : непосредственный // Технические науки: теория и практика : материалы I Междунар. науч. конф. (г. Чита, апрель 2012 г.). — Чита : Издательство Молодой ученый, 2012. — С. 98-105. — URL: https://moluch.ru/conf/tech/archive/7/2071/ (дата обращения: 24.04.2025).
- Криогенное пучение обусловлено теплофизическими и
физико-механическими закономерностями промерзания грунтов. Характер
процесса изменяется как в пространстве, так и во времени, поэтому
получила распространение точка зрения на криогенное пучение как на
стохастический процесс [1]. Достаточный уровень безопасности по
отношению к таким случайным природным воздействиям должен
обеспечиваться ещё на стадии проектирования.
- В качестве объекта исследования выбирается газопровод из стали 13Г1С-4 (к54), который имеет наружный диаметр D = 720 мм и толщину стенки трубы t = 14 мм. Для аппроксимации диаграммы деформирования материала используется методика, предложенная А.Б. Айнбиндером [2]. При этом зависимость
 схематично представляется в виде трех функций, соответствующих
участкам упругой работы, упруго-пластической работы и упрочнения
схематично представляется в виде трех функций, соответствующих
участкам упругой работы, упруго-пластической работы и упрочнения
- В работе [3] представлены результаты экспериментального исследования поведения мёрзлого грунта при различных скоростях деформирования. Для пучения можно воспользоваться данными при невысоких скоростях. Для определения жесткостных характеристик грунта в вертикальном направлении (вверх и вниз) проводится решение плоской задачи механики деформируемого твёрдого тела с использованием МКЭ-пакета ANSYS. При моделировании жесткости грунта в осевом (продольном) направлении коэффициент трения между мёрзлым грунтом и трубопроводом принят равным 0,9. Жесткостные характеристики грунта приведены в таблице 1.
- В качестве объекта исследования выбирается газопровод из стали 13Г1С-4 (к54), который имеет наружный диаметр D = 720 мм и толщину стенки трубы t = 14 мм. Для аппроксимации диаграммы деформирования материала используется методика, предложенная А.Б. Айнбиндером [2]. При этом зависимость
Таблица 1
Жесткостные характеристики мёрзлого грунта
|
Направление |
Жесткость, Н/мм2 |
Предельная сила, Н/мм |
|
Осевое (продольное) |
0,523 |
2,615 |
|
Вверх |
87,31 |
648,7 |
|
Вниз |
117,28 |
762,3 |
- На рассматриваемый газопровод действует следующая система нагрузок: 1) гравитационные силы; 2) внутреннее давление в трубе; 3) тепловое расширение; 4) нагрузки, возникающие при морозном пучении грунта.
- Гравитационная нагрузка учитывается путем задания ускорения силы тяжести и соответствующей массовой плотности материала трубы. Кроме того, здесь учитывается вес газа и изоляции. Внутреннее (рабочее) давление в трубе
 МПа.
Температура замыкания трубопровода равна минус 5оС, а
температура продукта составляет 40оС.
МПа.
Температура замыкания трубопровода равна минус 5оС, а
температура продукта составляет 40оС.- Основными для данной трубопроводной системы являются нагрузки, обусловленные пучением грунта. В настоящее время оценка непосредственно сил морозного пучения затруднительна, поэтому здесь предпочтительно задавать невозмущенный профиль пучения в виде функции вертикального перемещения грунта при свободном пучении (т.е. при отсутствии трубопровода и засыпки) от продольной координаты.
- Пусть на рассматриваемом участке трубопровода морозное пучение грунта происходит в виде образования системы одиночных бугров пучения, удаленных друг от друга настолько, что их совместным влиянием на изгиб трубопровода можно пренебречь. Тогда решение поставленной задачи сводится к решению серии задач о взаимодействии трубопровода с единичным бугром пучения.
- Реальный бугор пучения будем аппроксимировать расчётным бугром прямоугольной формы высотой
 и длиной
и длиной
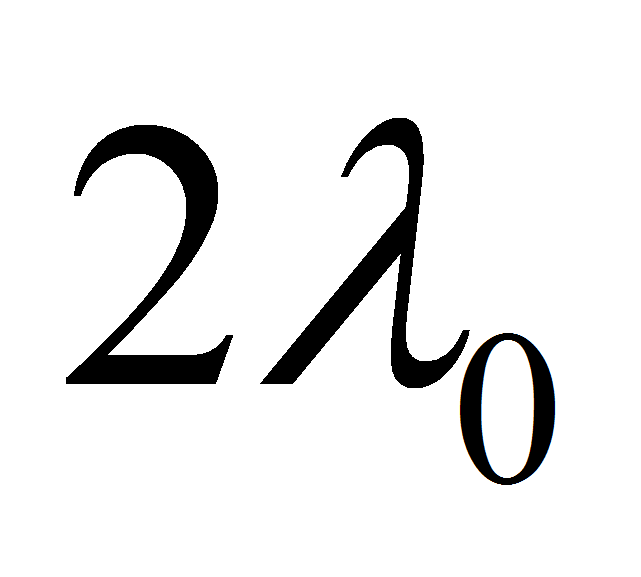 (рисунок 1). Поскольку мёрзлый грунт не является абсолютно жёстким,
происходит частичное смятие бугра за счет сил, действующих со
стороны трубопровода. Очевидно, что при некотором значении этих сил
из-за текучести грунта становится невозможным подрастание бугра
пучения.
(рисунок 1). Поскольку мёрзлый грунт не является абсолютно жёстким,
происходит частичное смятие бугра за счет сил, действующих со
стороны трубопровода. Очевидно, что при некотором значении этих сил
из-за текучести грунта становится невозможным подрастание бугра
пучения.- Основное требование к трубопроводам как транспортным системам повышенной ответственности с точки зрения обеспечения безопасности состоит в сохранении герметичности и конструктивной целостности в течение всего срока службы [4].
- Таким образом, нарушение герметичности оболочки трубопровода означает безусловное наступление предельного состояния, т.е. такого состояния, при котором дальнейшая эксплуатация трубопроводной системы невозможна по соображениям безопасности и/или неприемлемых экономических затрат на продолжение эксплуатации.
- В то же время для потенциально опасных сооружений и конструкций (к которым принадлежат газо- и нефтепроводы) к категории предельных могут быть отнесены пограничные состояния, реализация которых приводит к существенному повышению риска возникновения критических и/или катастрофических отказов. К таким состояниям могут быть отнесены предельные состояния, сформированные в традиционном для строительной механики смысле.
- На рассматриваемый газопровод действует следующая система нагрузок: 1) гравитационные силы; 2) внутреннее давление в трубе; 3) тепловое расширение; 4) нагрузки, возникающие при морозном пучении грунта.
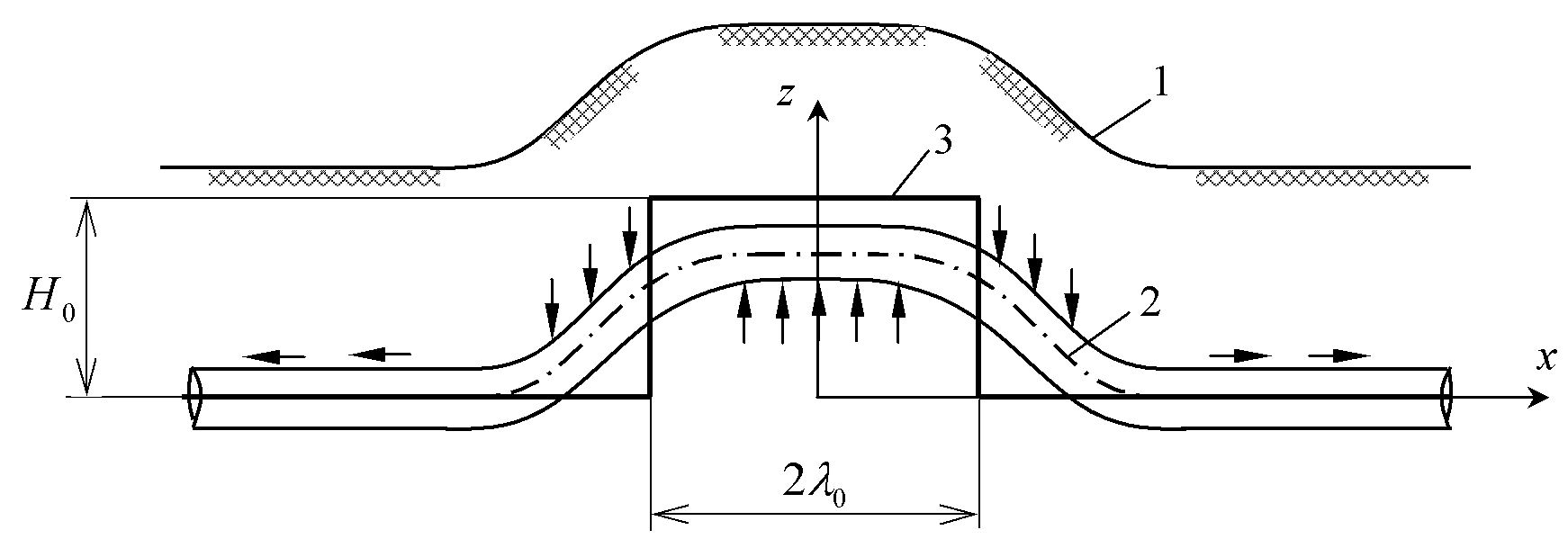
Рисунок 1 – Взаимодействие трубопровода с единичным бугром
пучения:
1 – земная поверхность; 2 – изогнутая ось
трубопровода; 3 – невозмущенный
профиль пучения
-
- Выделим два типа предельных состояний. Предельное состояние типа I свяжем с наступлением текучести. В качестве наиболее жесткого критерия наступления этого предельного состояния примем появление пластических деформаций хотя бы в одной точке поперечного сечения. Данный критерий запишем в следующем виде:
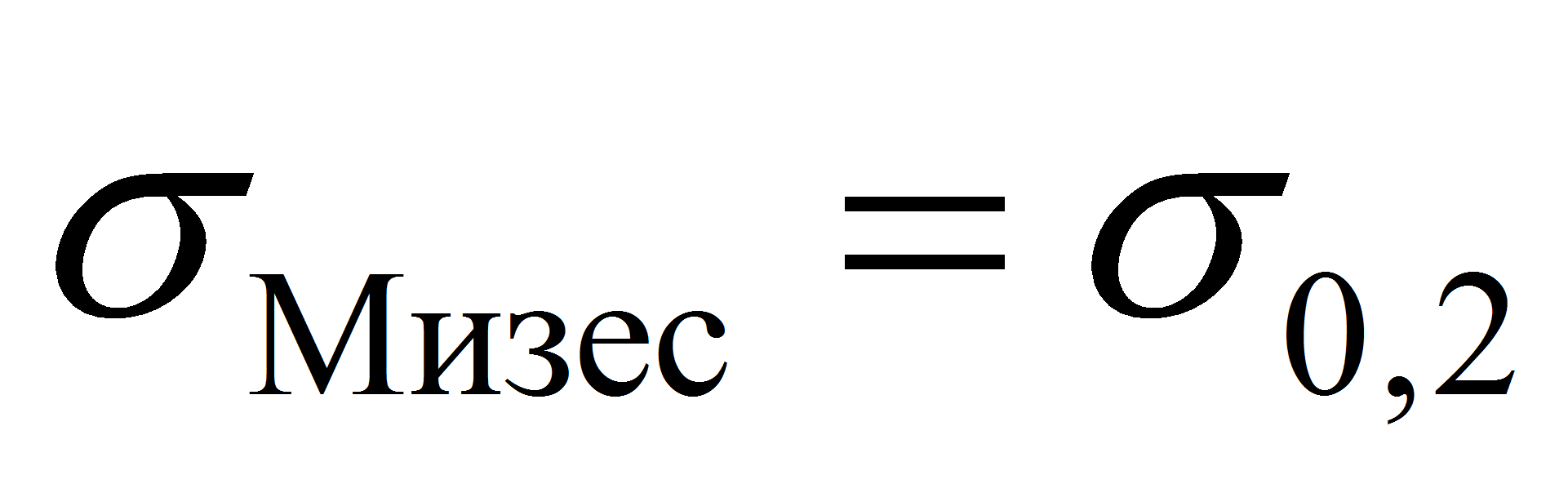 ,
(1)
,
(1)- где
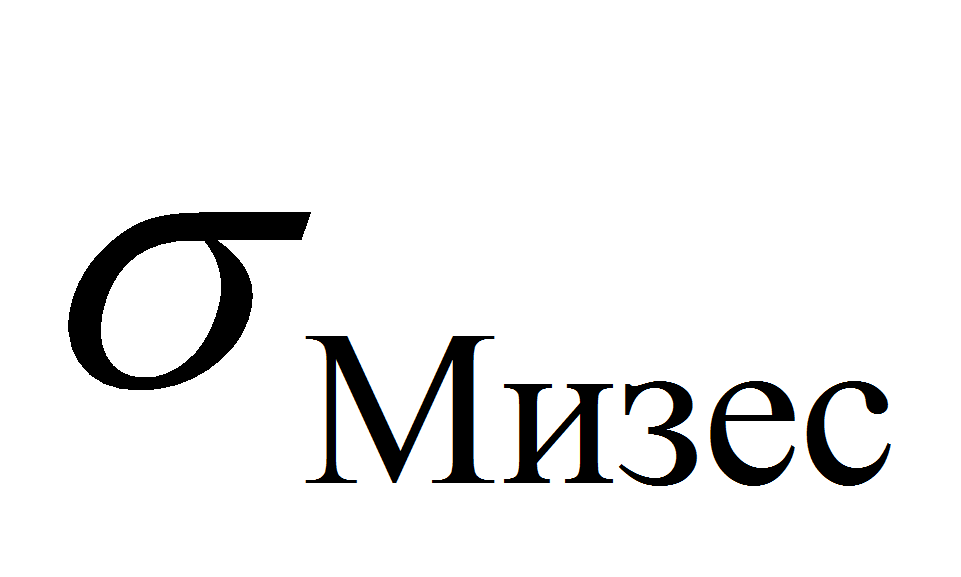 – напряжение по Мизесу (или эквивалентное напряжение по теории
прочности энергии формоизменения);
– напряжение по Мизесу (или эквивалентное напряжение по теории
прочности энергии формоизменения);
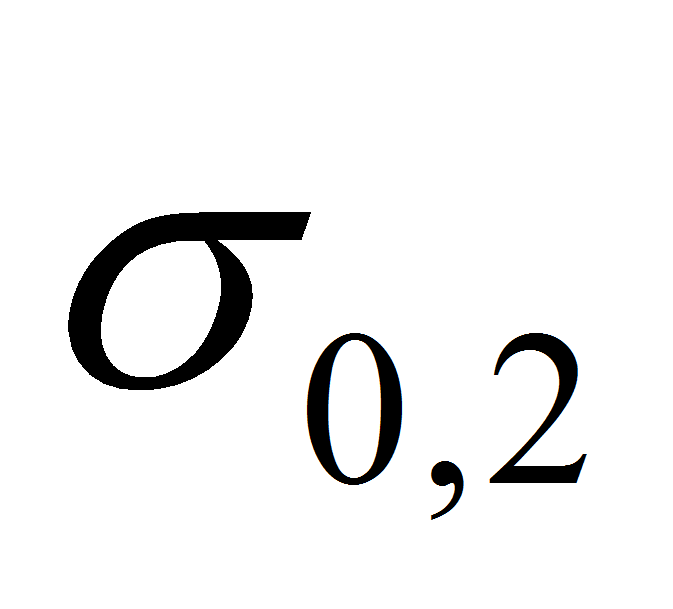 – условный предел текучести. Для рассматриваемого газопровода
– условный предел текучести. Для рассматриваемого газопровода
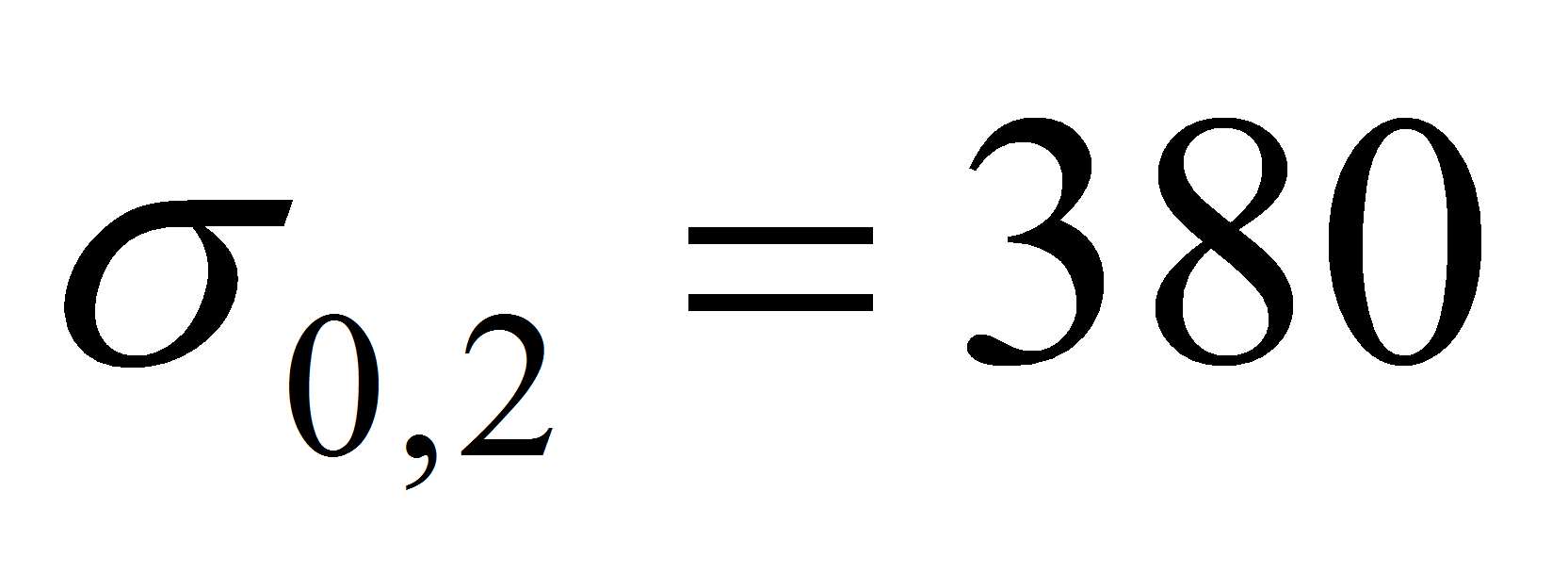 МПа.
МПа.- Предельное состояние типа II свяжем с резким снижением несущей способности трубопровода, обусловленным образованием пластического шарнира или местной потерей устойчивости оболочки трубы (гофрообразованием) в сжатой зоне поперечного сечения. Критерий наступления предельного состояний типа II может быть записан как
 или
или
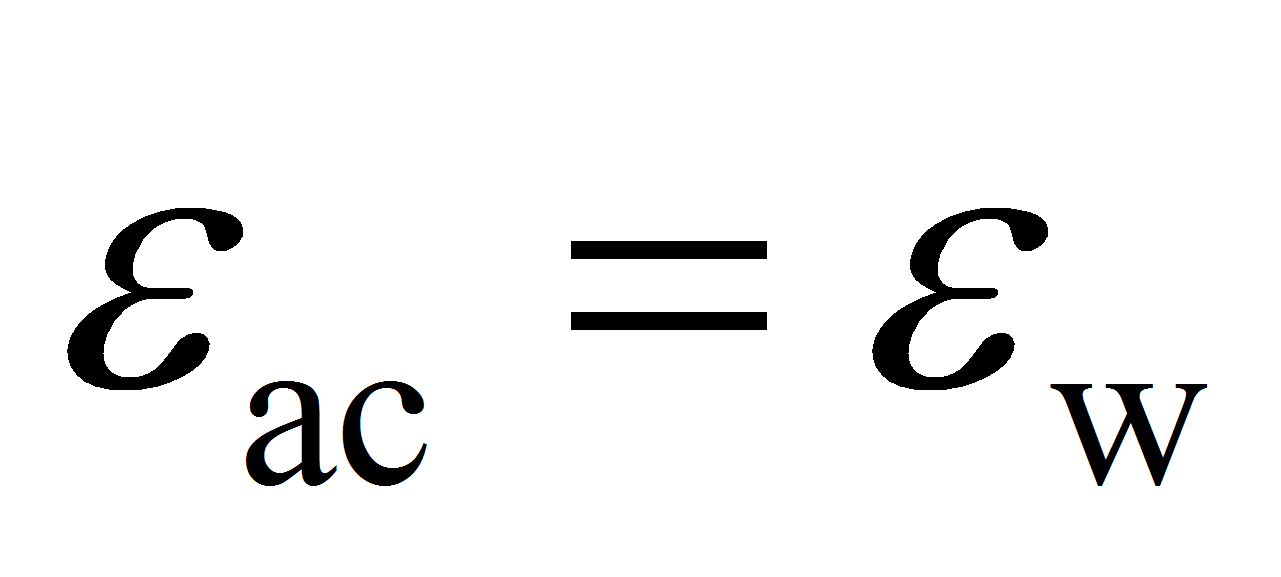 ,
(2)
,
(2)- где
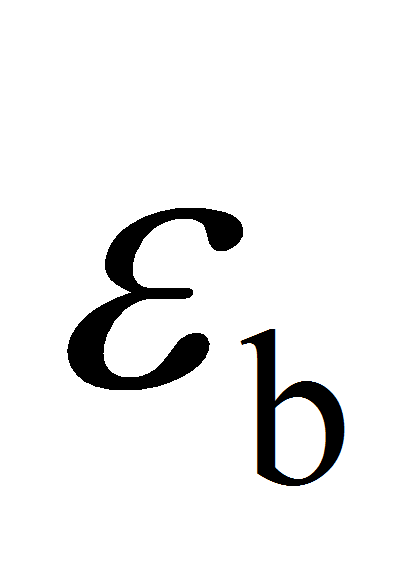 – деформация изгиба трубы;
– деформация изгиба трубы;
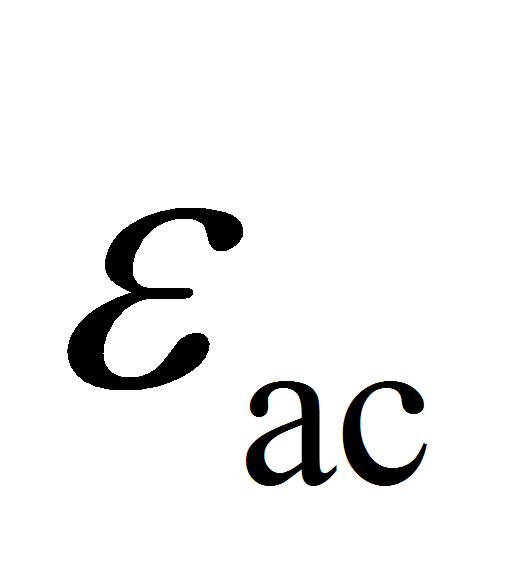 – осевая (фибровая) деформация сжатия;
– осевая (фибровая) деформация сжатия;
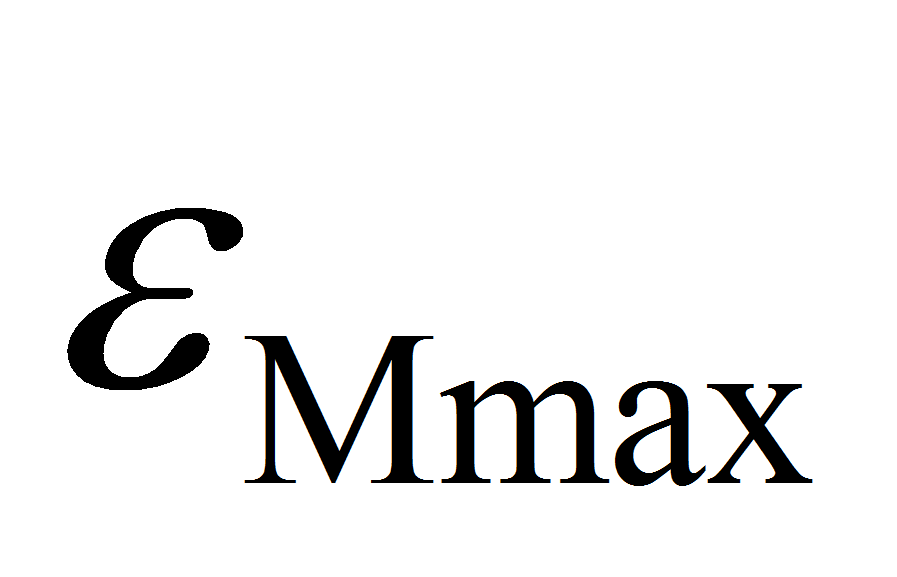 – деформация, соответствующая максимуму на кривой «момент
– деформация»;
– деформация, соответствующая максимуму на кривой «момент
– деформация»;
 – деформация сжатия, при которой начинается гофрообразование.
– деформация сжатия, при которой начинается гофрообразование.- Следует отметить, что наступление предельных состояний данных типов не приводит к непосредственному нарушению герметичности конструкции и тем самым наступлению критического отказа. Однако при этом создаются предпосылки для возникновения критических отказов вследствие реализации непроектных режимов функционирования трубопровода.
- Деформация
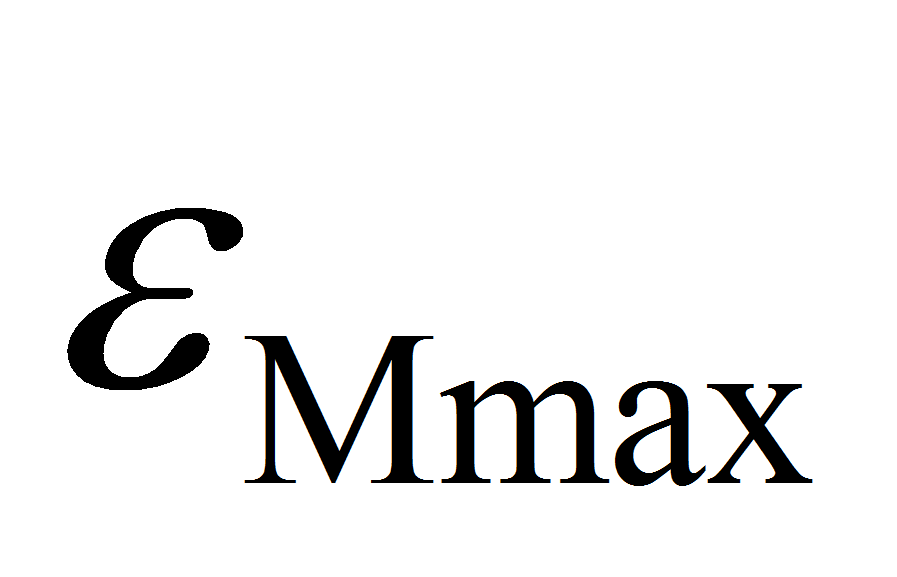 может быть определена с помощью нелинейного МКЭ-анализа чистого
изгиба трубы. При этом для учета возможного сплющивания поперечного
сечения здесь следует воспользоваться оболочечной моделью. Как
показывают результаты решения данной задачи в МКЭ-пакете ANSYS,
для рассматриваемой трубы 720х14 можно принять
может быть определена с помощью нелинейного МКЭ-анализа чистого
изгиба трубы. При этом для учета возможного сплющивания поперечного
сечения здесь следует воспользоваться оболочечной моделью. Как
показывают результаты решения данной задачи в МКЭ-пакете ANSYS,
для рассматриваемой трубы 720х14 можно принять
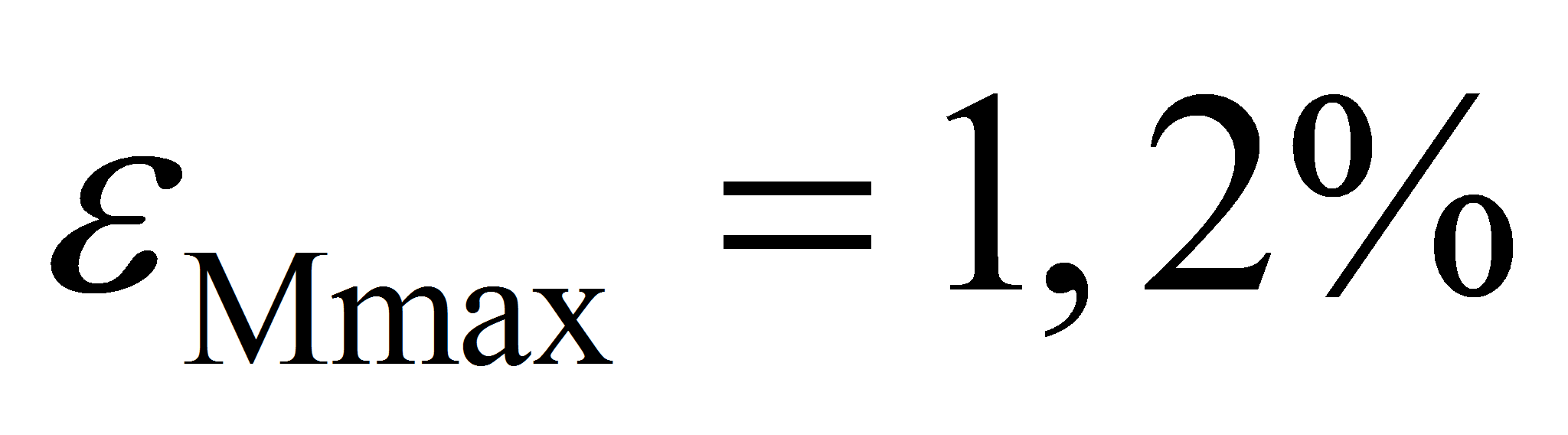 .
Деформация
.
Деформация
 ,
рассчитанная по представленной в работе [3] методике, составляет
минус 2,11%.
,
рассчитанная по представленной в работе [3] методике, составляет
минус 2,11%.- Одним из самых трудоёмких этапов настоящего исследования является моделирование силового воздействия бугра пучения на подземный трубопровод. Решение данной задачи должно проводиться в геометрически и физически нелинейной статической постановке, т.е. с учетом больших перемещений, пластических деформаций и нелинейности поведения окружающего трубу грунта. Для этих целей также используется МКЭ-пакет ANSYS, причем для автоматизации процесса решения разработана программа-макрос heaving.mac. Благодаря симметрии здесь можно ограничиться моделированием только правой половины бугра пучения с размерами
 и
и
 (см. рисунок 1). Для того чтобы граничные условия на правом конце
трубы не имели значительного влияния на критическую область вблизи
бугра пучения, длина модели должна быть достаточно большой.
(см. рисунок 1). Для того чтобы граничные условия на правом конце
трубы не имели значительного влияния на критическую область вблизи
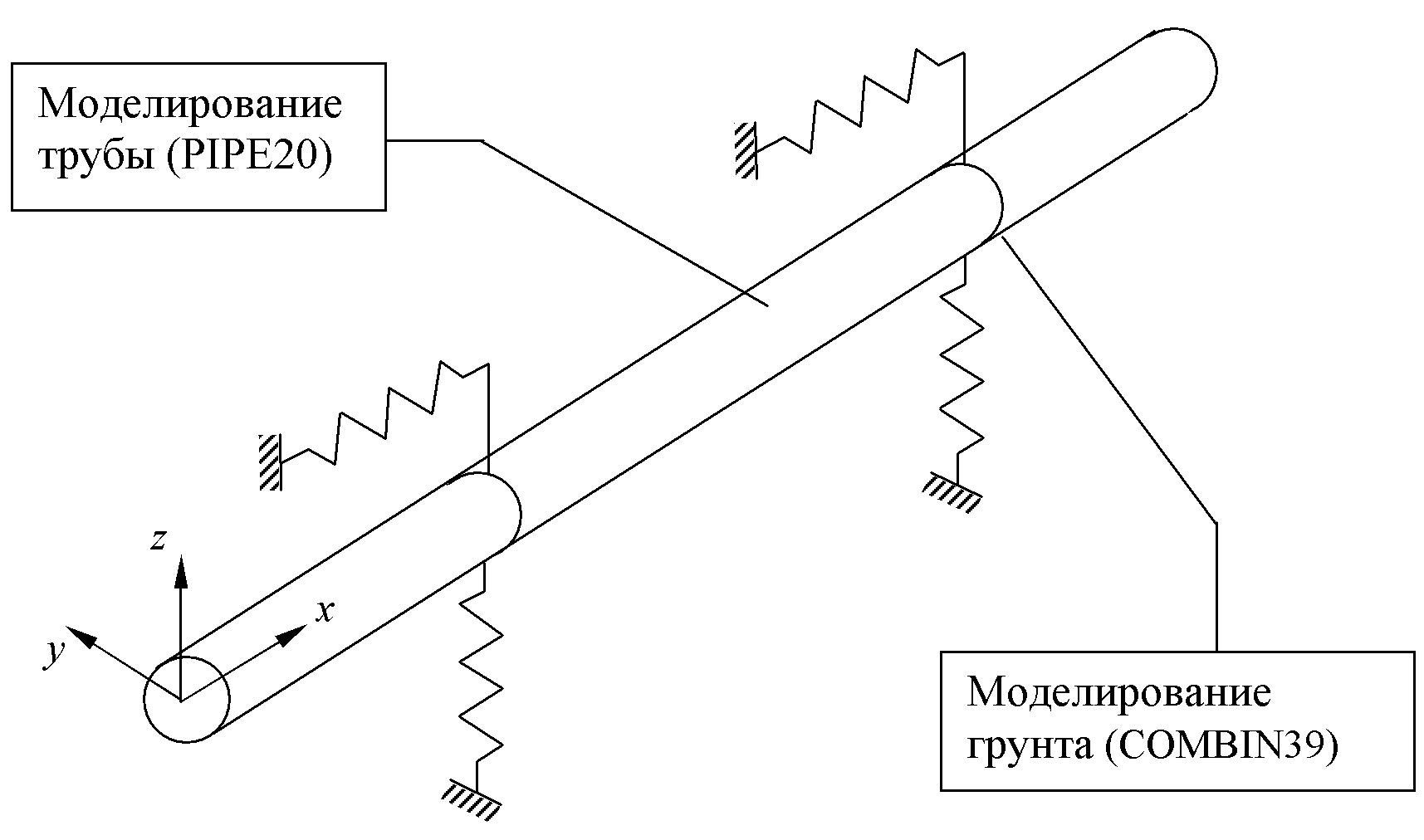
бугра пучения, длина модели должна быть достаточно большой.- Для данной модели используются два типа конечных элементов: элемент пластической трубы PIPE20 и элемент нелинейной пружины COMBIN39, предназначенный для дискретного представления точек грунта. Последний элемент определяется двумя узлами и кривой деформирования (зависимостью силы, возникающей в пружине, от относительного перемещения его узлов). Одним концом пружина крепится к элементу трубы, другим – к опоре (рисунок 2).
- Выделим два типа предельных состояний. Предельное состояние типа I свяжем с наступлением текучести. В качестве наиболее жесткого критерия наступления этого предельного состояния примем появление пластических деформаций хотя бы в одной точке поперечного сечения. Данный критерий запишем в следующем виде:
Рисунок 2 – Представление грунта с помощью дискретных
элементов-пружин
-
- Учитывая, что здесь рассматривается лишь деформирование в вертикальной плоскости, каждый узел трубы, необходимо связать с неподвижной опорой с помощью двух элементов-пружин, представляющих жёсткости грунта в продольном (осевом) и вертикальном направлениях. Следует отметить, что использование элементов-пружин в геометрически нелинейном анализе связано с определёнными трудностями. В результате больших перемещений они могут испытывать значительные отклонения от их правильной ориентации, что может привести к появлению не существующих в действительности компонентов сил. Длина пружин должна быть такой, чтобы эти нежелательные компоненты оставались в приемлемых с точки зрения точности пределах. В данной программе длина элементов COMBIN39 выбрана равной 25 м.
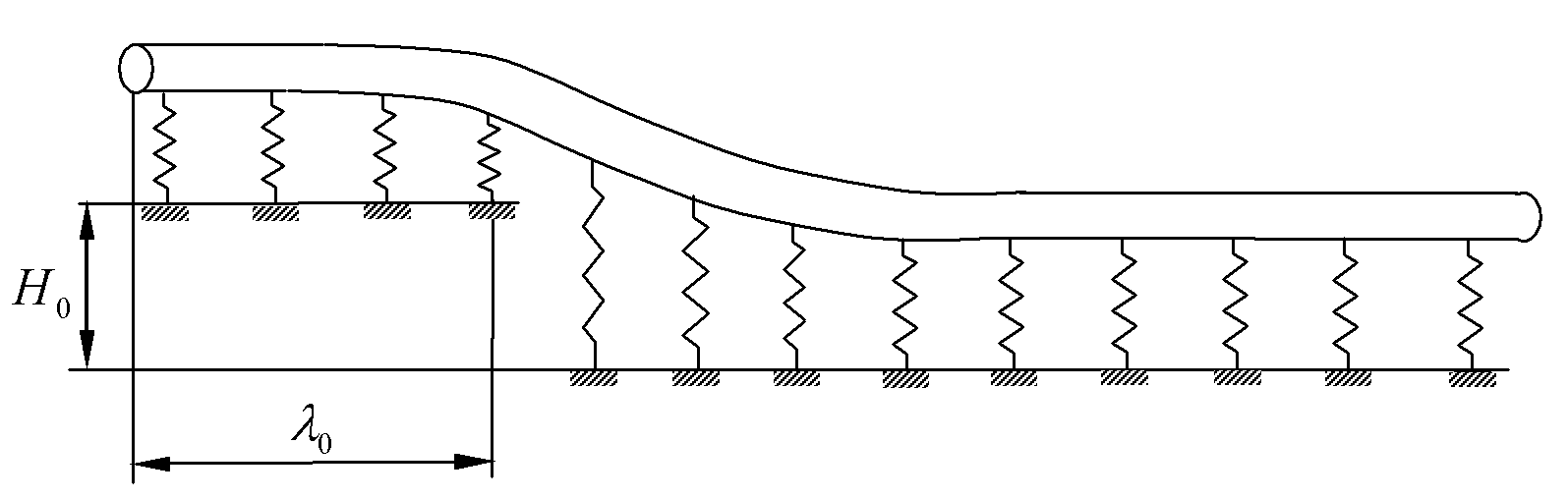
- Моделирование бугра пучения осуществляется путём задания в положительном направлении оси
 постоянного на длине
постоянного на длине
 смещения
смещения
 ,
которое прикладывается к свободным концам элементов-пружин,
имитирующих действие грунта (рисунок 3).
,
которое прикладывается к свободным концам элементов-пружин,
имитирующих действие грунта (рисунок 3).
- Учитывая, что здесь рассматривается лишь деформирование в вертикальной плоскости, каждый узел трубы, необходимо связать с неподвижной опорой с помощью двух элементов-пружин, представляющих жёсткости грунта в продольном (осевом) и вертикальном направлениях. Следует отметить, что использование элементов-пружин в геометрически нелинейном анализе связано с определёнными трудностями. В результате больших перемещений они могут испытывать значительные отклонения от их правильной ориентации, что может привести к появлению не существующих в действительности компонентов сил. Длина пружин должна быть такой, чтобы эти нежелательные компоненты оставались в приемлемых с точки зрения точности пределах. В данной программе длина элементов COMBIN39 выбрана равной 25 м.
Рисунок 3 – Моделирование смещения бугра пучения
-
- Следует отметить, что по окончании работы макроса heaving.mac автоматически определяется наиболее нагруженное сечение трубопровода, в диаметрально противоположных точках которого имеют место максимальное
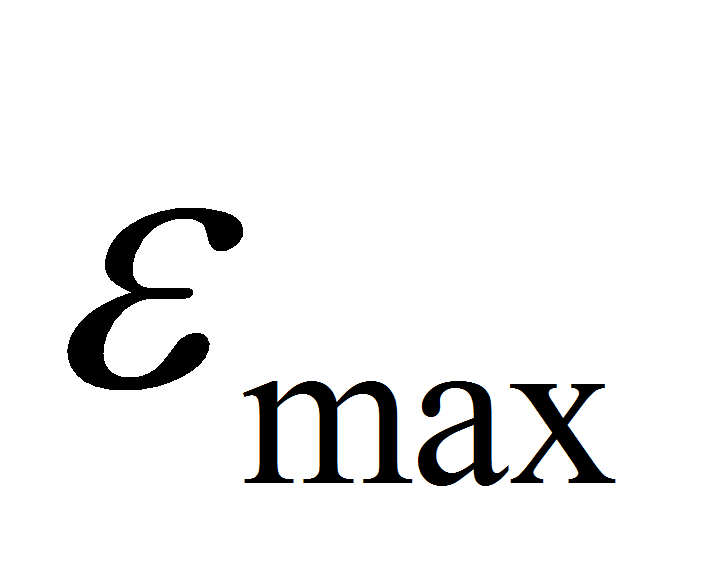 и минимальное
и минимальное
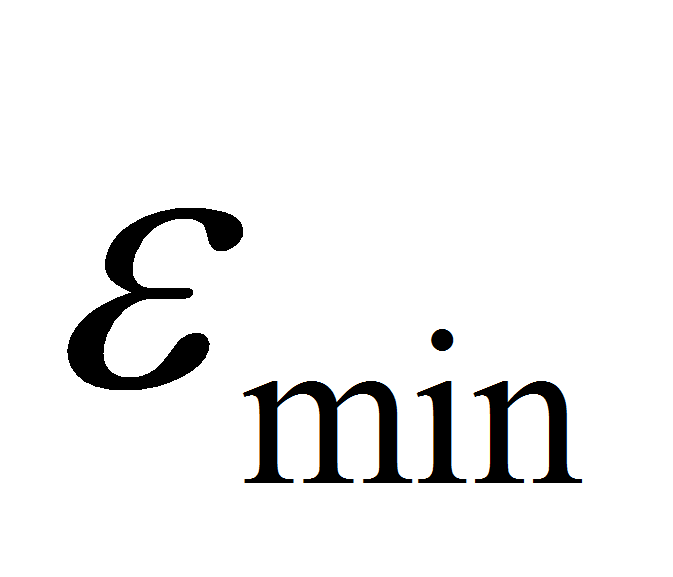 значения осевых деформаций. По этим значения рассчитываются
деформация изгиба
значения осевых деформаций. По этим значения рассчитываются
деформация изгиба
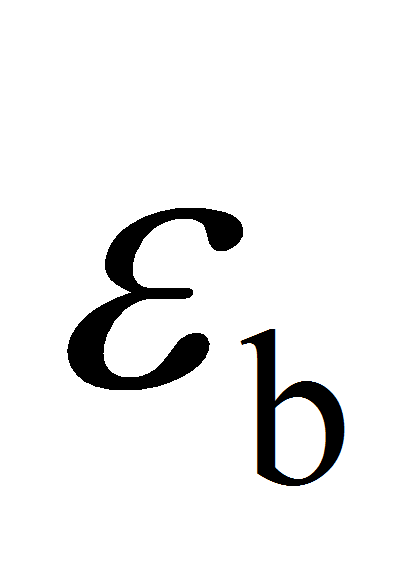 и осевая деформация сжатия
и осевая деформация сжатия
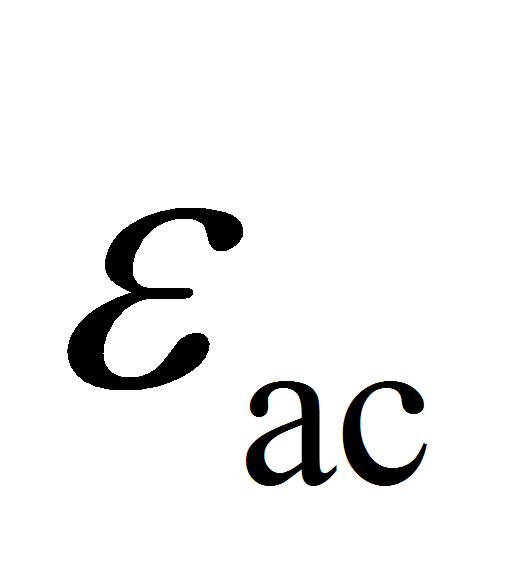 ,
которые используются в критериях (1) и (2).
,
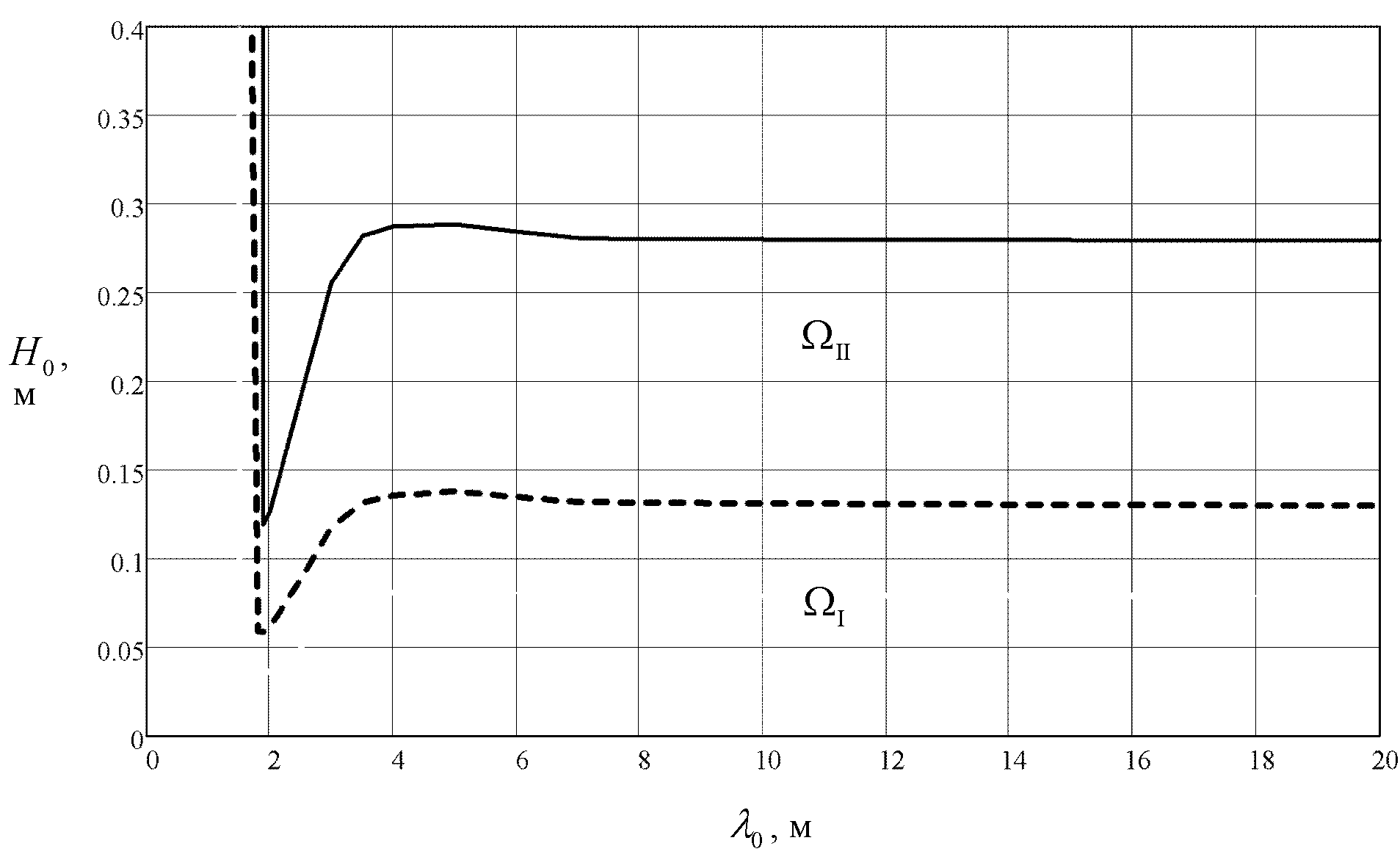
которые используются в критериях (1) и (2).- Предельные состояния для рассматриваемого газопровода 720х14 изображены на рисунке 4, причём штриховая линия соответствует предельному состоянию типа I (возникновение пластических деформаций), а сплошная – состоянию типа II (резкое снижение несущей способности). Очевидно, что области допустимых размеров бугров пучения
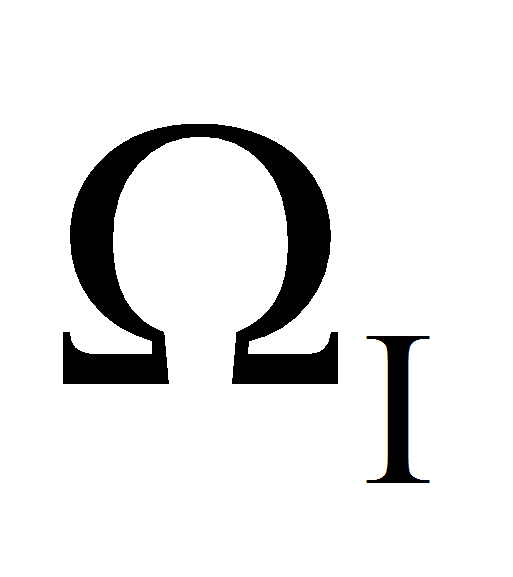 и
и
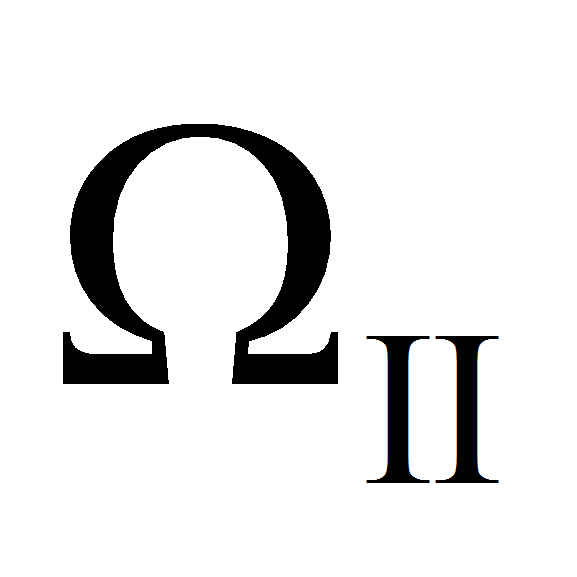 ,
соответствующие двум введённым ранее критериям, располагаются под
этими кривыми, которые выступают в роли их предельных границ.
,
соответствующие двум введённым ранее критериям, располагаются под
этими кривыми, которые выступают в роли их предельных границ.- Если оценивать работоспособность рассматриваемого газопровода по критерию типа II (сплошная линия на рисунке 4), то видно, что наиболее опасными для него являются бугры пучения длиной 3,8 м (
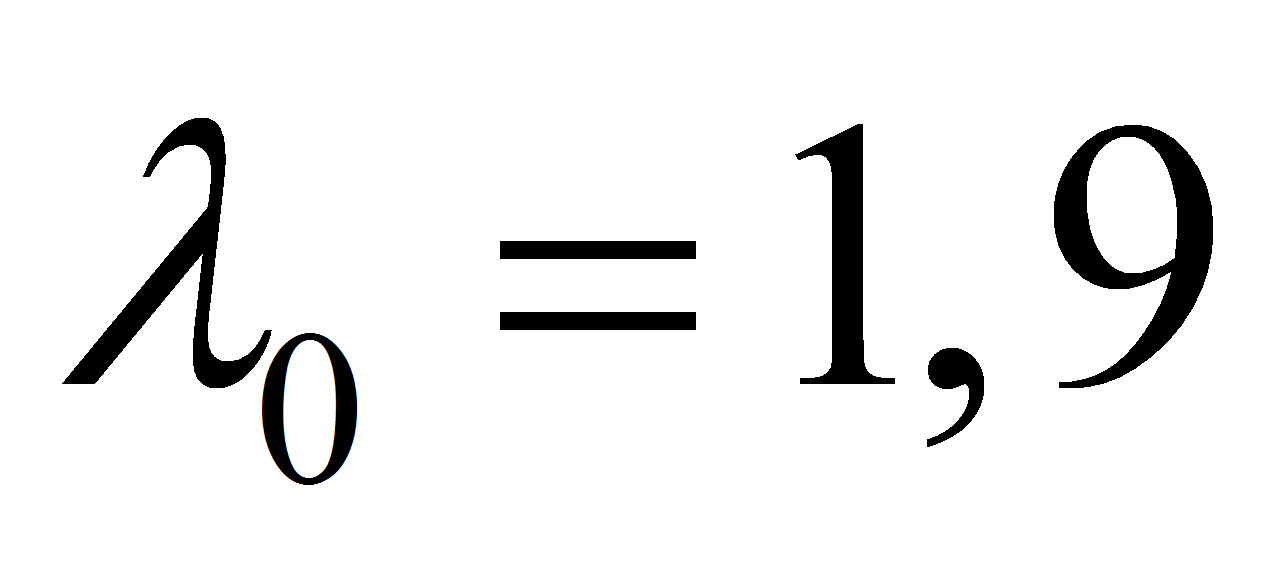 м), причём бугры меньшей длины сминаются трубопроводом до
наступления в нём предельного состояния типа II,
и поэтому они вообще не представляют какой-либо опасности вне
зависимости от высоты бугра.
м), причём бугры меньшей длины сминаются трубопроводом до
наступления в нём предельного состояния типа II,
и поэтому они вообще не представляют какой-либо опасности вне
зависимости от высоты бугра.
- Следует отметить, что по окончании работы макроса heaving.mac автоматически определяется наиболее нагруженное сечение трубопровода, в диаметрально противоположных точках которого имеют место максимальное
Рисунок 4 – Области допустимых размеров бугров пучения
-
- Решение задачи статистической динамики здесь проводится метод интерполяционных полиномов, который является наиболее экономичным. В качестве случайных входных данных выбираются две величины, оказывающие наибольшее влияние на напряжённо-деформированное состояние трубопровода: высота
 и полудлина
и полудлина
 бугра пучения. Предполагается, что они не коррелируют между собой и
подчиняются нормальному закону распределения. Их числовые
характеристики приняты следующими: математические ожидания
бугра пучения. Предполагается, что они не коррелируют между собой и
подчиняются нормальному закону распределения. Их числовые
характеристики приняты следующими: математические ожидания
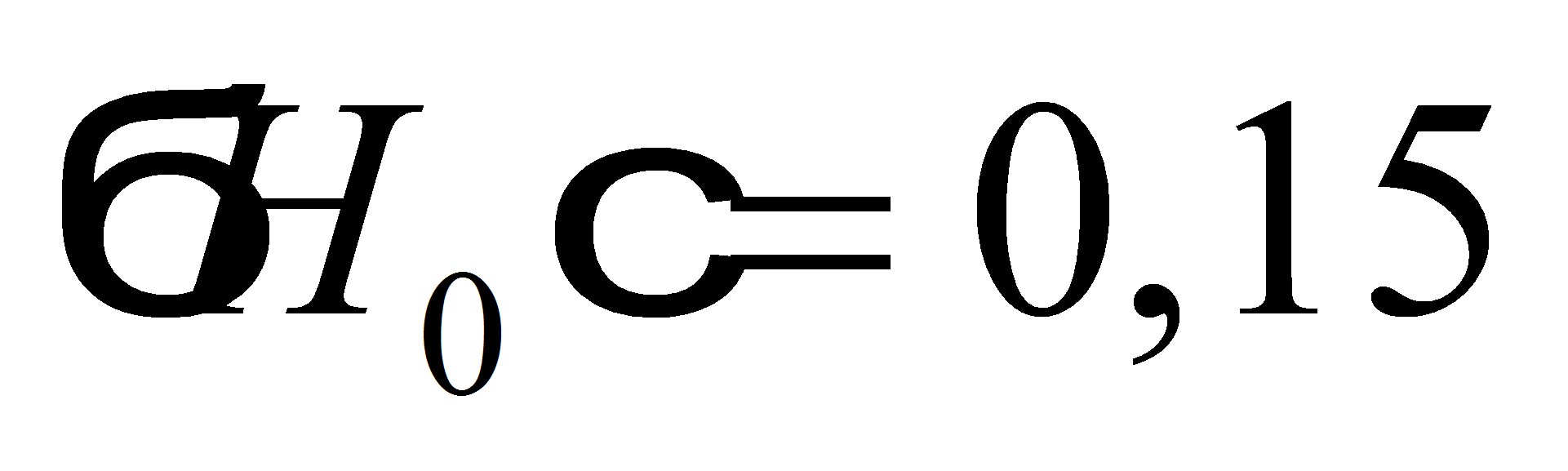 м
и
м
и
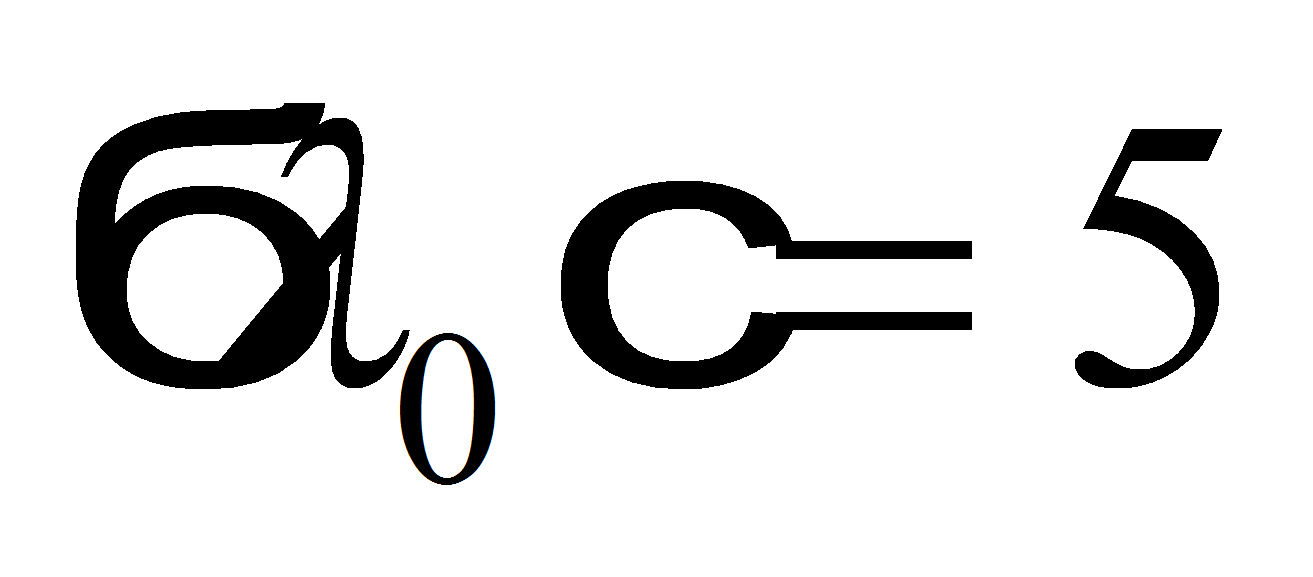 м;
средние квадратические отклонения
м;
средние квадратические отклонения
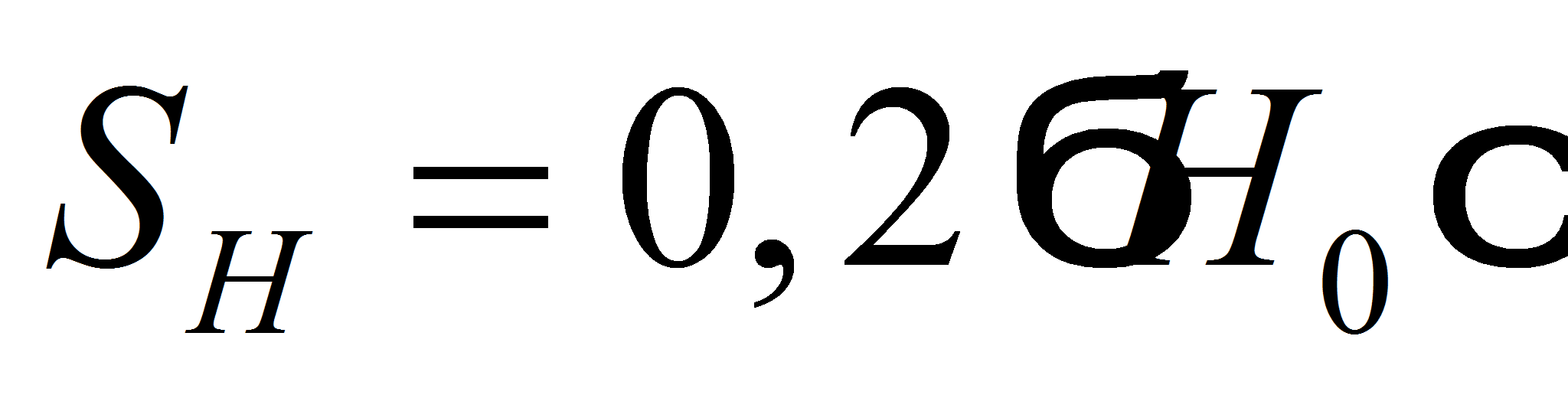 и
и
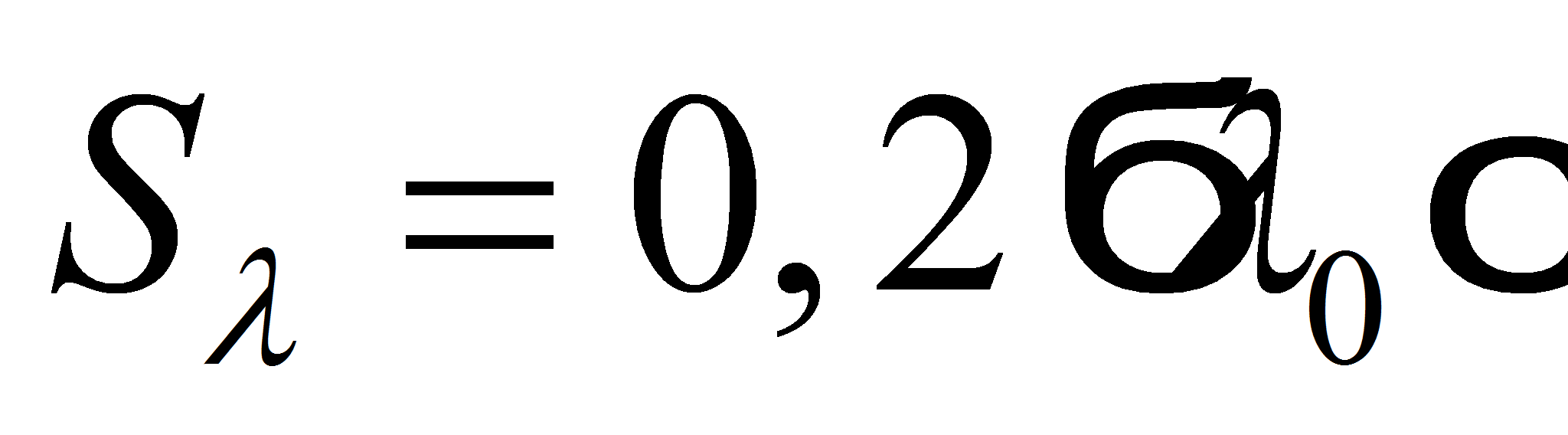 .
.- Для каждой входной случайной величины задаётся по пять узлов интерполирования (схема 5х5). При этом значения xj случайной величины x, распределённой по нормальному закону, определяются по следующей формуле:
 , (3)
, (3)- где
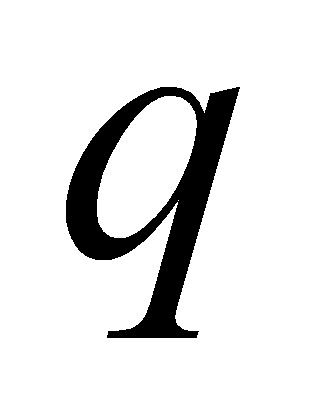 – число узлов интерполирования (в нашем случае
– число узлов интерполирования (в нашем случае
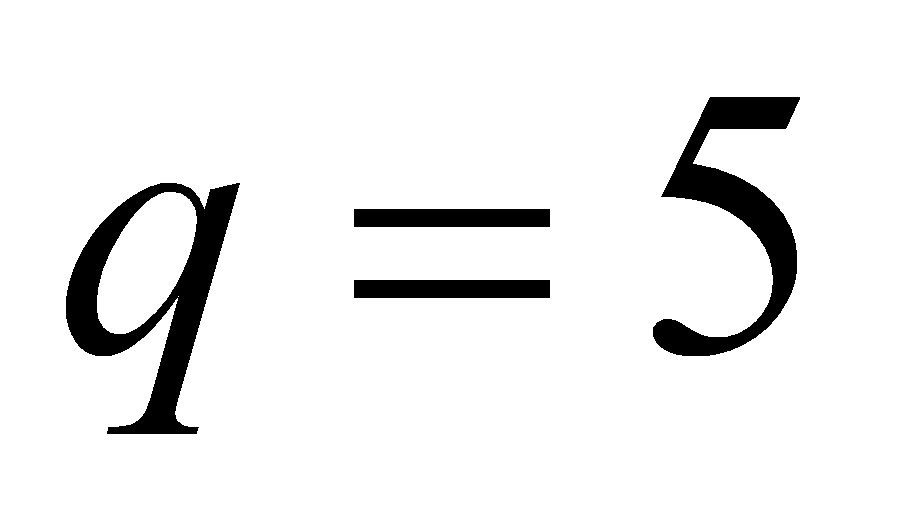 );
);
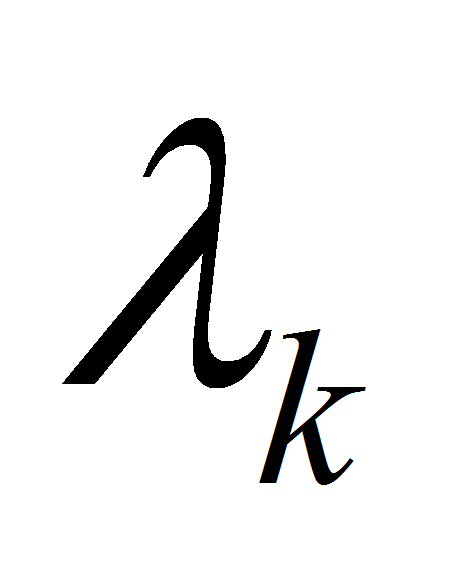 – координаты узлов типа Чебышева.
– координаты узлов типа Чебышева.- Следует отметить, что в методе интерполяционных полиномов математическое ожидание и среднее квадратическое отклонение некоторой выходной случайной величины
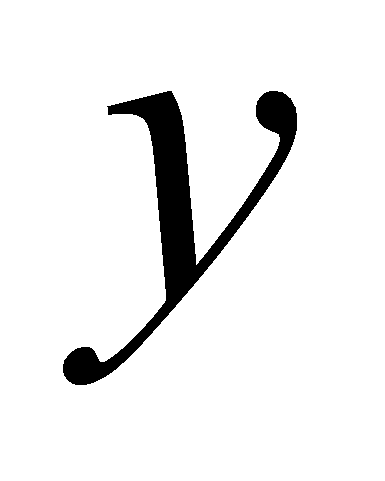 находятся по формулам
находятся по формулам (4)
(4)- где
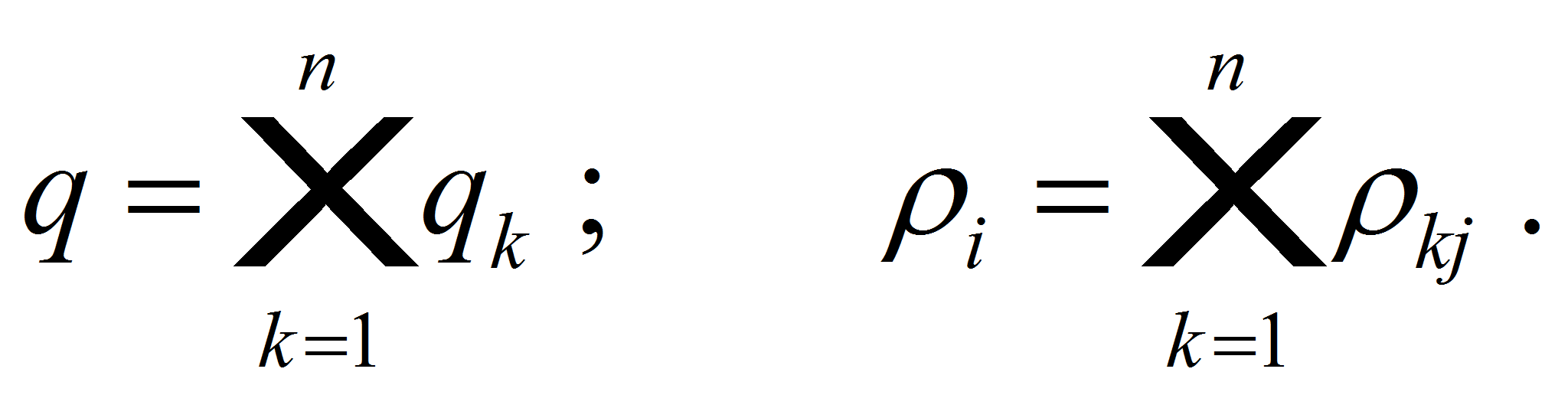
- Здесь
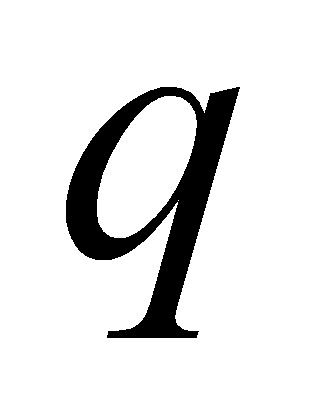 – общее число реализаций;
– общее число реализаций;
 – значение выходной случайной величины на i-ой
реализации;
– значение выходной случайной величины на i-ой
реализации;
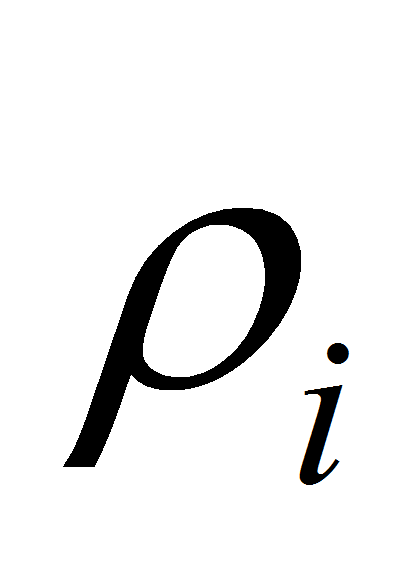 – число Кристоффеля выходной случайной величины; n
– число входных случайных величин;
– число Кристоффеля выходной случайной величины; n
– число входных случайных величин;
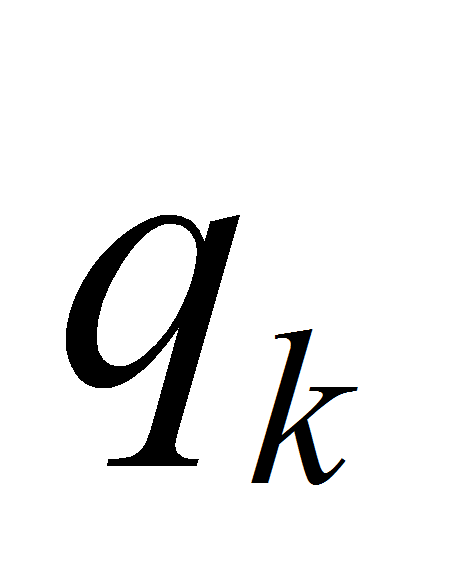 – число узлов интерполирования, выбранное для k-ой
входной случайной величины;
– число узлов интерполирования, выбранное для k-ой
входной случайной величины;
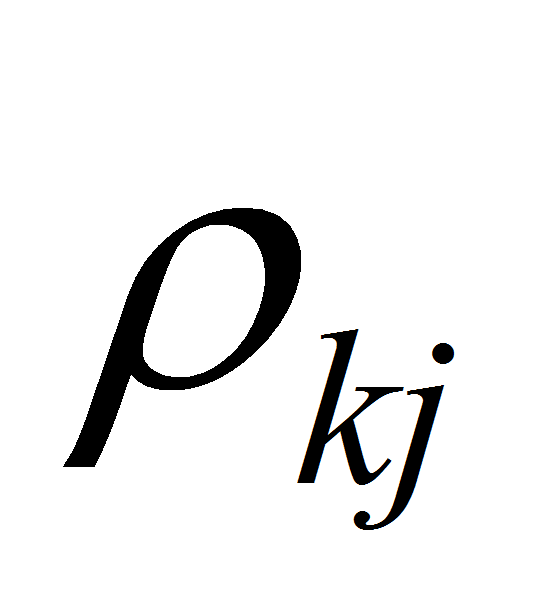 – числа Кристоффеля для k-ой
входной случайной величины.
– числа Кристоффеля для k-ой
входной случайной величины.- Для выходных случайных величин вычисленные по формулам (4) математические ожидания и средние квадратические отклонения сведены в таблицу 2.
- Решение задачи статистической динамики здесь проводится метод интерполяционных полиномов, который является наиболее экономичным. В качестве случайных входных данных выбираются две величины, оказывающие наибольшее влияние на напряжённо-деформированное состояние трубопровода: высота
Таблица 2
Математические ожидания и средние квадратические отклонения выходных случайных величин
|
Характеристики случайной величины |
||||
|
0,247% |
-0,940% |
0,594% |
379,1 МПа |
|
|
0,0626% |
0,279% |
0,171% |
10,01 МПа |
|
|
0,253 |
0,297 |
0,288 |
0,0264 |
- Вызывающие аварийные ситуации природные воздействия (такие как землетрясения, ураганы, оползни, пучения и просадки грунта и т.д.) не поддаются контролю, и поэтому достаточный уровень безопасности по отношению к ним должен быть обеспечен на стадии проектирования. Следует отметить, что в расчетах на безопасность широко применяются вероятностные модели редких событий. Для оценки показателей безопасности и риска рассматриваемой конструкции воспользуемся теорией, предложенной В.В. Болотиным [5].
- Функцией безопасности
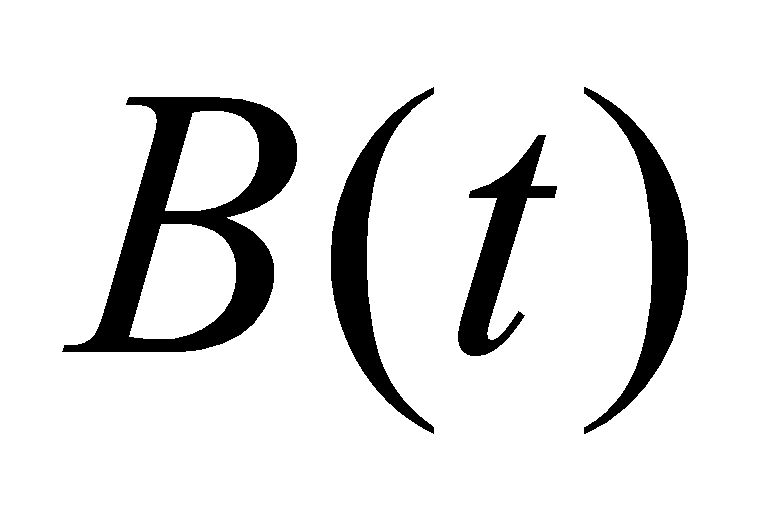 называется вероятность того, что на отрезке времени [0, t]
ни разу не возникнет аварийная ситуация:
называется вероятность того, что на отрезке времени [0, t]
ни разу не возникнет аварийная ситуация: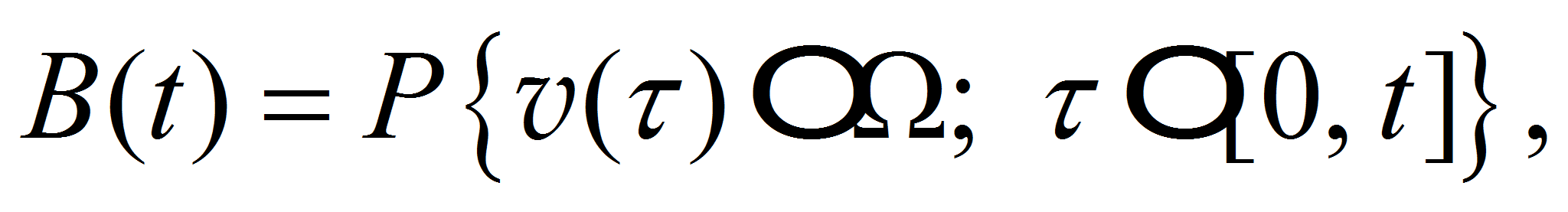 (5)
(5)- где v(τ) может совпадать с вектором качества, входящим в определение для вероятности безотказной работы. Здесь Ω – область безопасности, которая включает в себя допустимую область по отношению к эксплуатационным отказам и предельным состояниям. Дополнение функции безопасности до единицы называется функцией риска
 (6)
(6)- Для вычисления функции безопасности при рассмотрении только одного класса событий
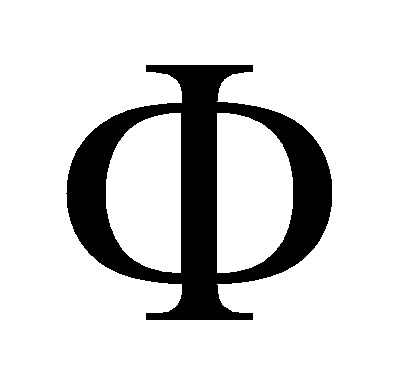 ,
связанного с возникновением бугров пучения, можно воспользоваться
следующей формулой [5]:
,
связанного с возникновением бугров пучения, можно воспользоваться
следующей формулой [5]: (7)
(7)- где
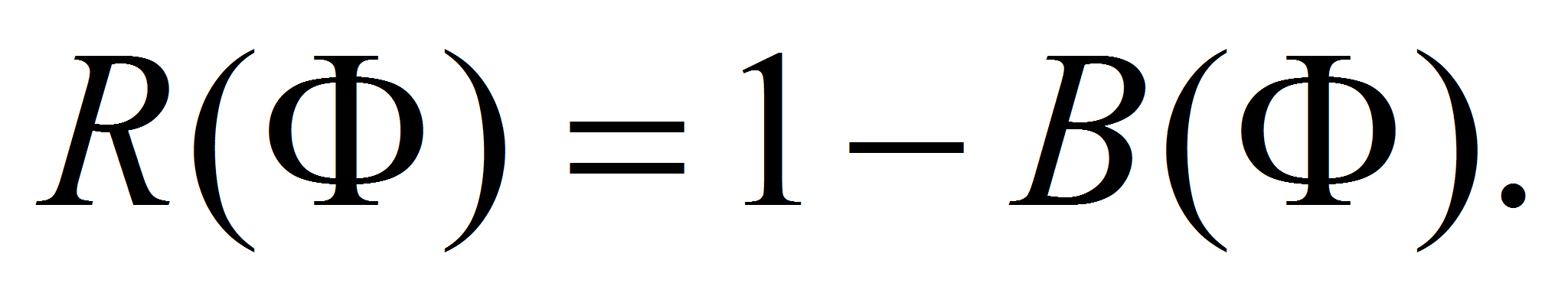 (8)
(8)- Здесь
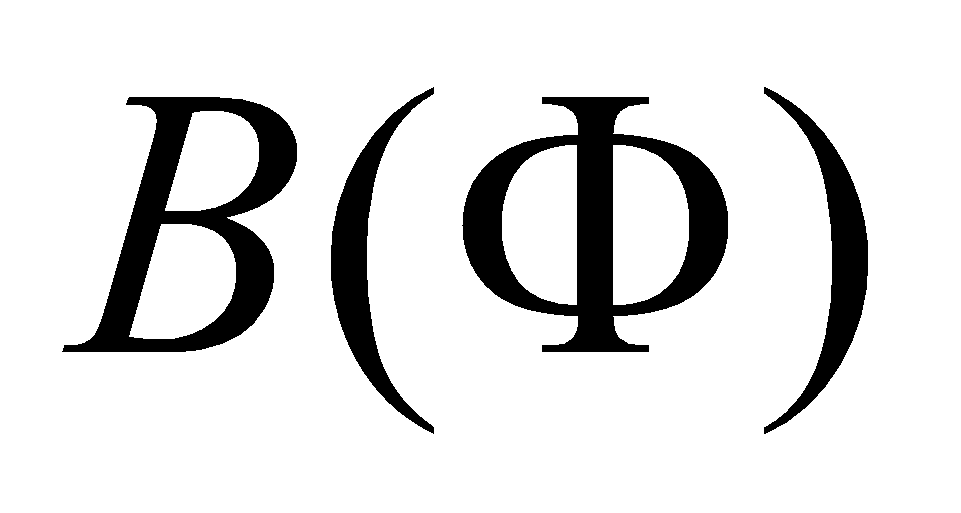 – условная безопасность, равная вероятности того, что авария
не наступит при появлении бугра пучения;
– условная безопасность, равная вероятности того, что авария
не наступит при появлении бугра пучения;
 – условный риск;
– условный риск;
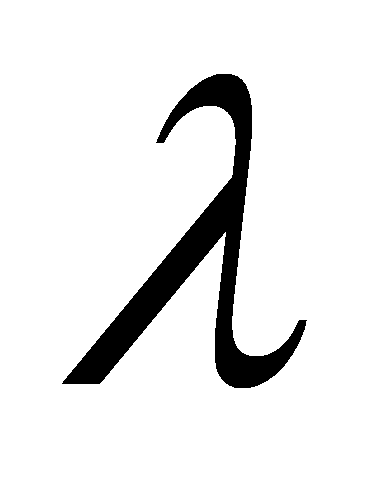 – математическое ожидание числа бугров пучения в единицу
времени на рассматриваемом участке трубопровода. Примем
– математическое ожидание числа бугров пучения в единицу
времени на рассматриваемом участке трубопровода. Примем
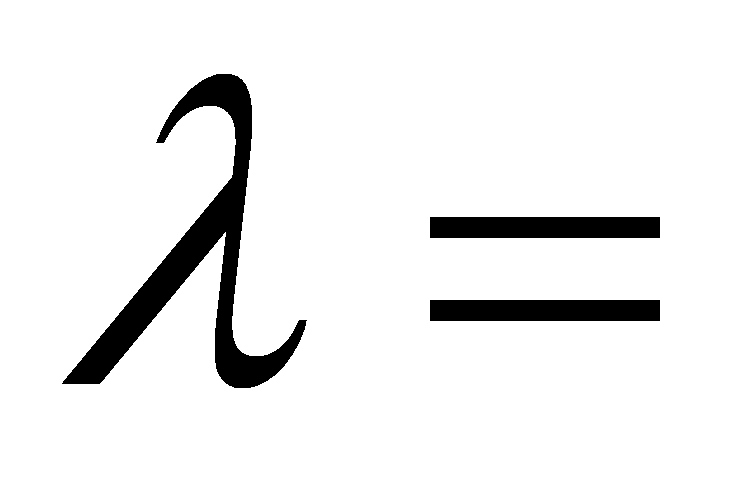 0,1 год-1.
0,1 год-1.- Условные показатели безопасности можно трактовать как вероятности не наступления предельных состояний типа I или II:
 (9)
(9)- Эти соотношения можно представить в более удобной для практического использования форме. Учитывая, что вектор качества системы квазимонотонно приближается к границам допустимых областей, запишем
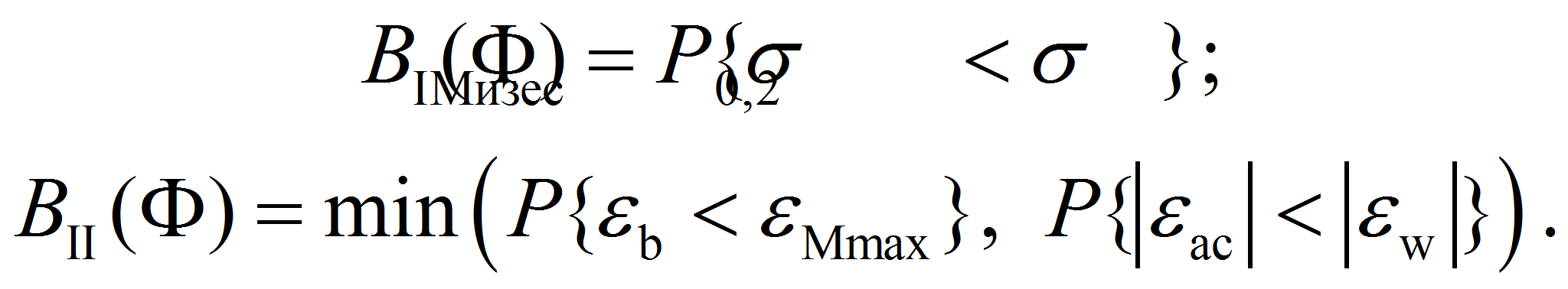 (10)
(10)- Входящие в эти выражения вероятности легко находятся с помощью функций распределения соответствующих выходных параметров.
- Как известно, функция распределения случайной величины Y определяется равенством
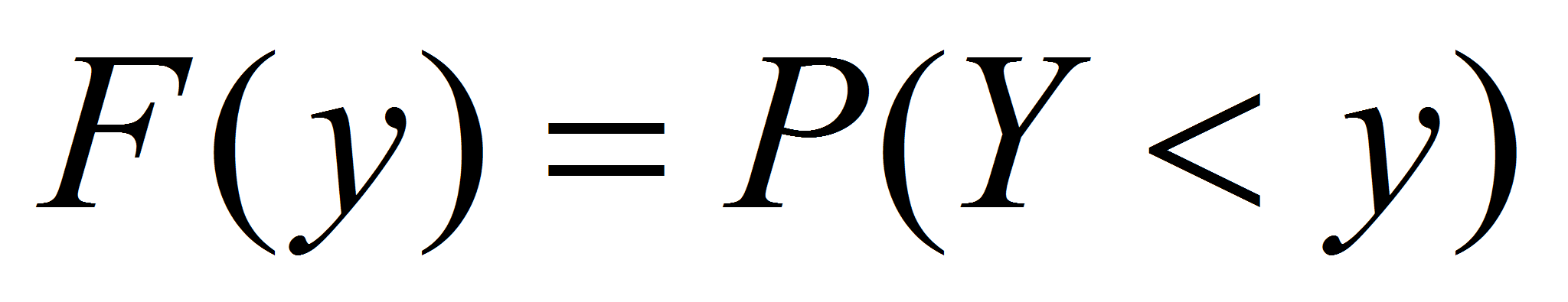 (11)
(11)- и равна вероятности того, что случайная величина принимает значение, меньшее
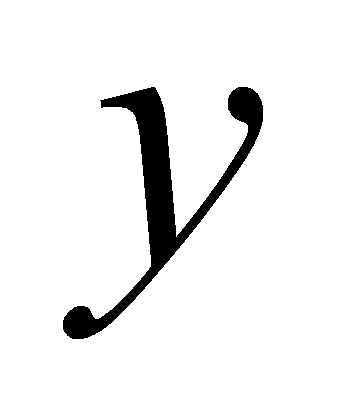 .
В методе интерполяционных полиномов для построения функции
распределения выходного параметра его значения следует расположить в
порядке возрастания
.
В методе интерполяционных полиномов для построения функции
распределения выходного параметра его значения следует расположить в
порядке возрастания
- где
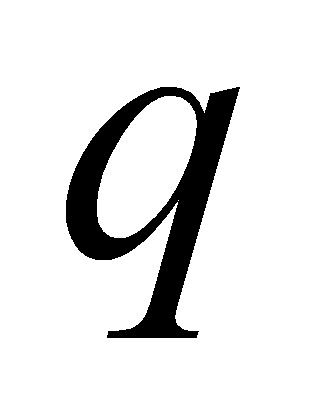 – общее число реализаций. Пусть этим значениям
соответствуют числа Кристоффеля
– общее число реализаций. Пусть этим значениям
соответствуют числа Кристоффеля
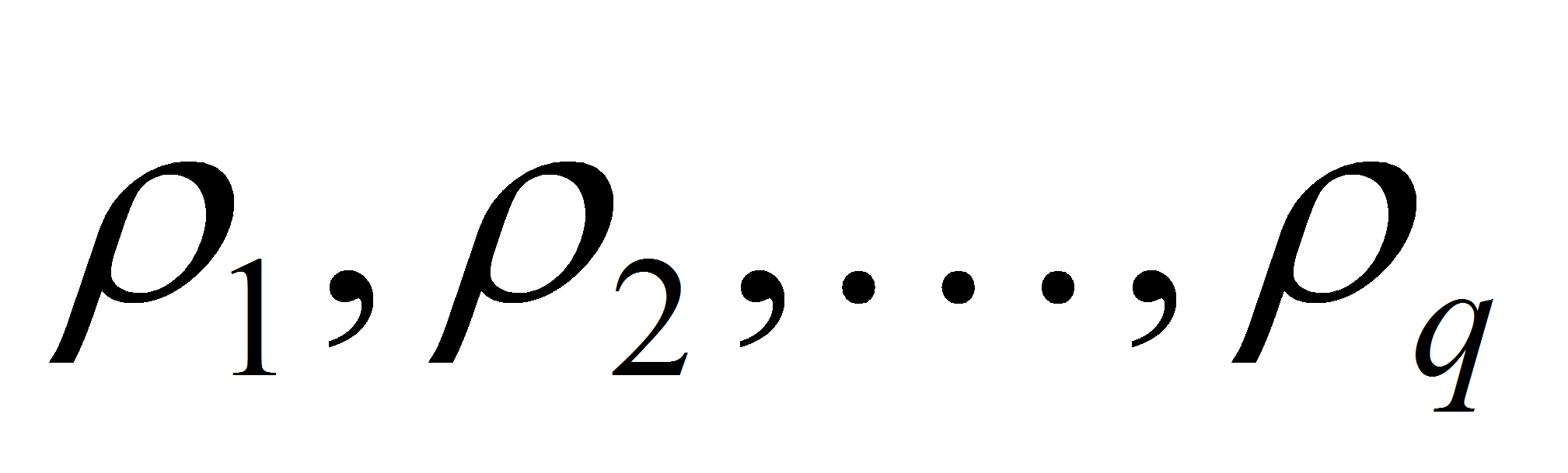 .
Тогда
.
Тогда
- и так далее, т.е.
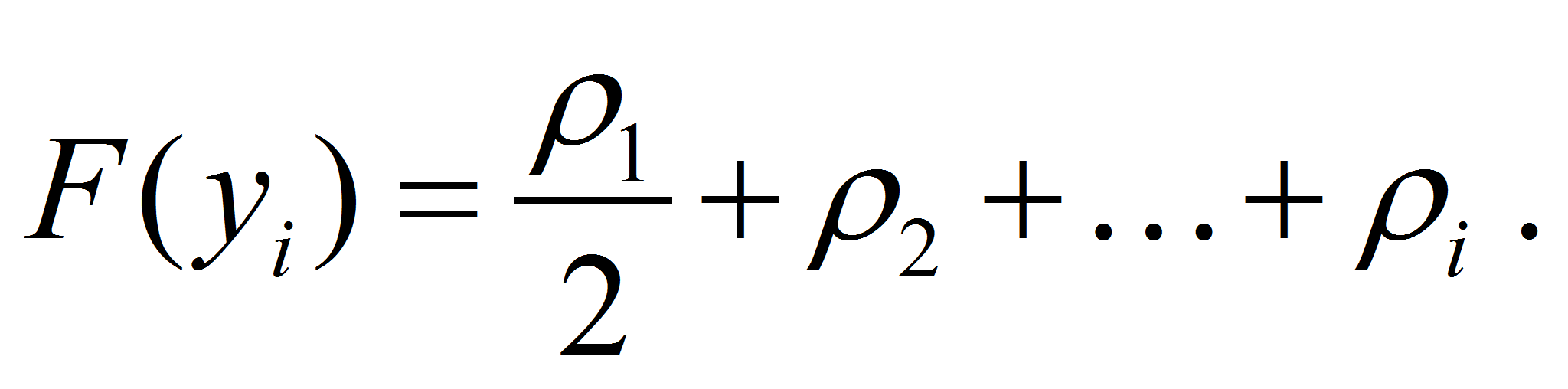
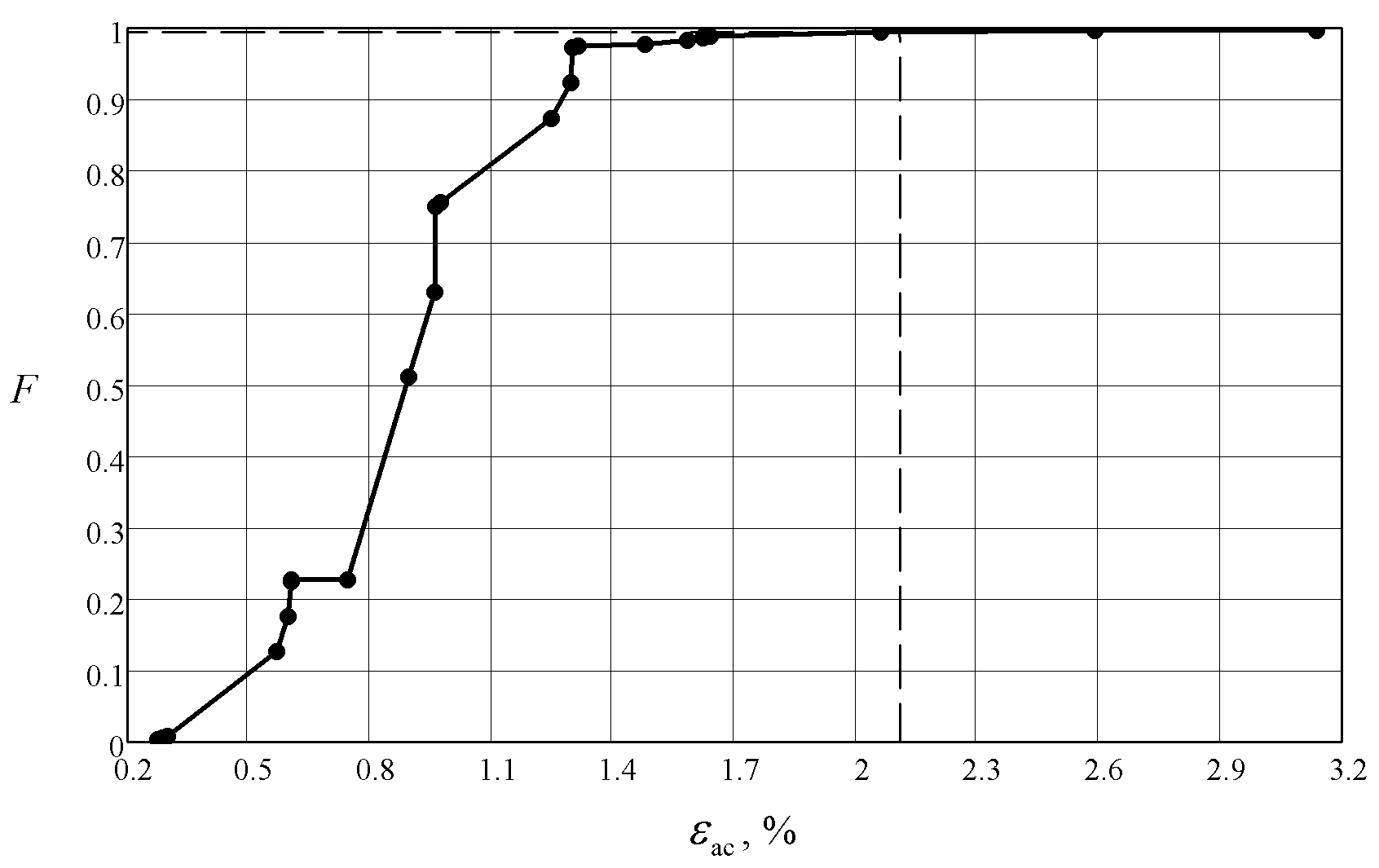
- Для рассматриваемых в данной задаче выходных случайных величин функции распределения изображены на рисунках 5…7. Сопоставляя эти кривые с допускаемыми значениями (
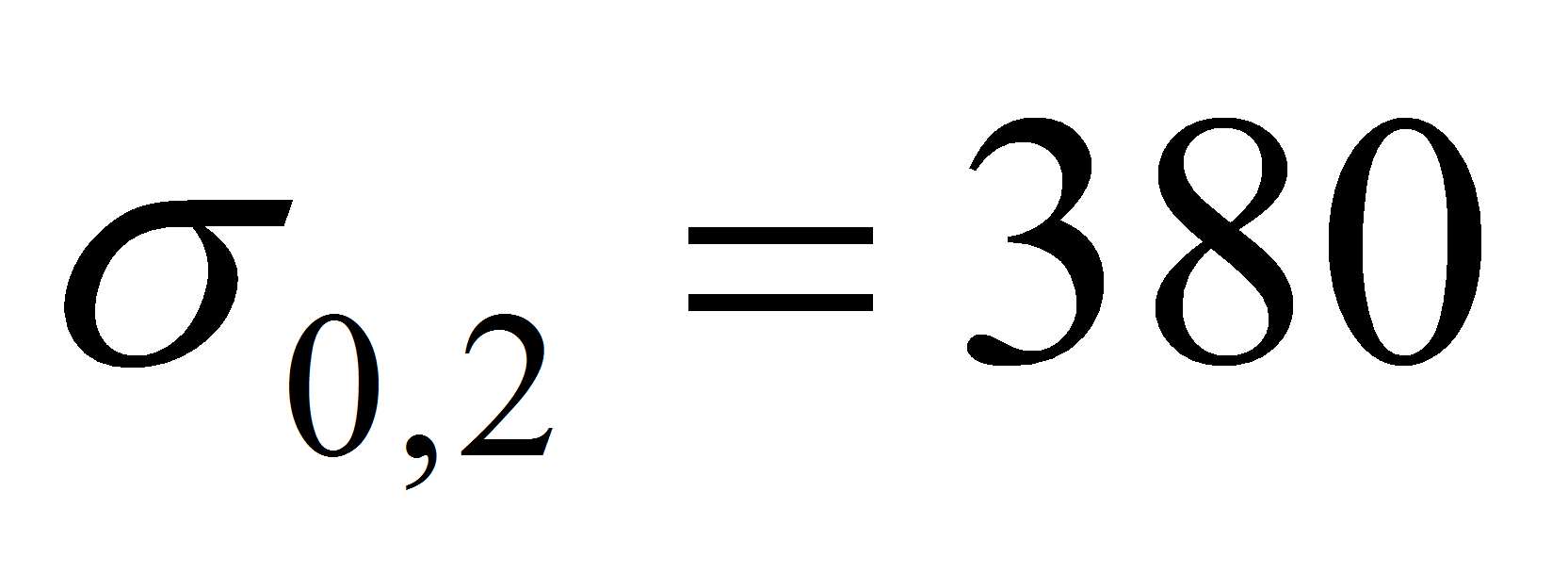 МПа;
МПа;
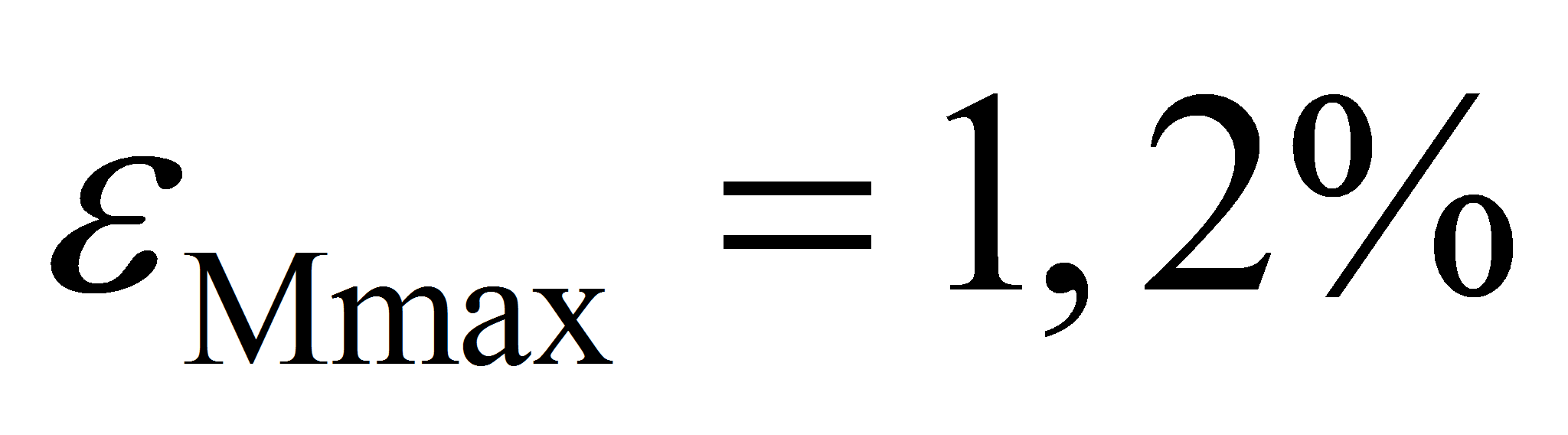 ;
;
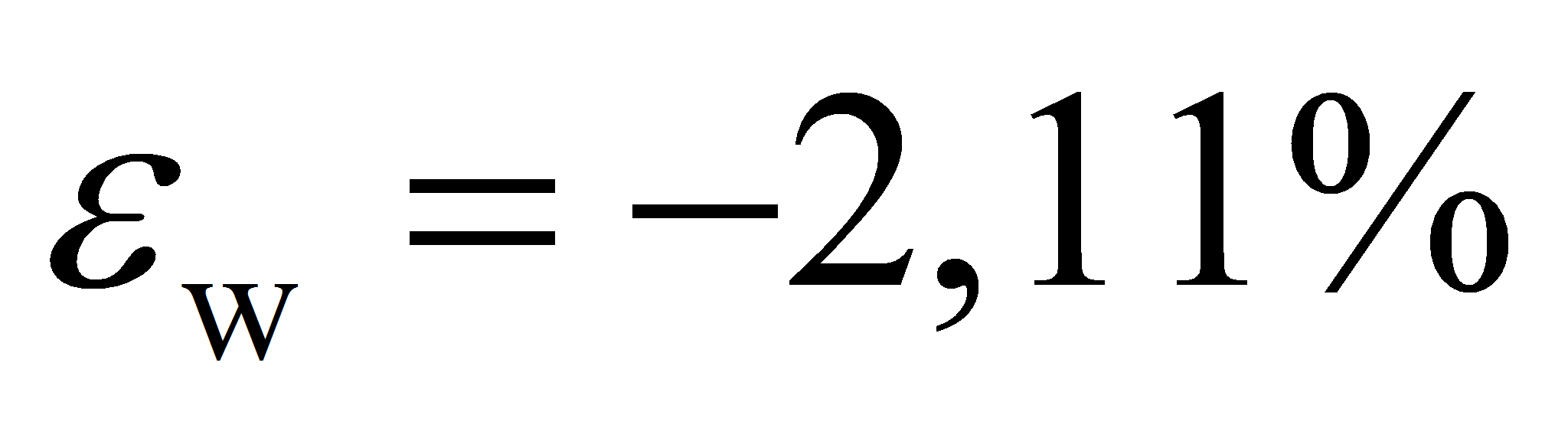 ),
можно найти:
),
можно найти: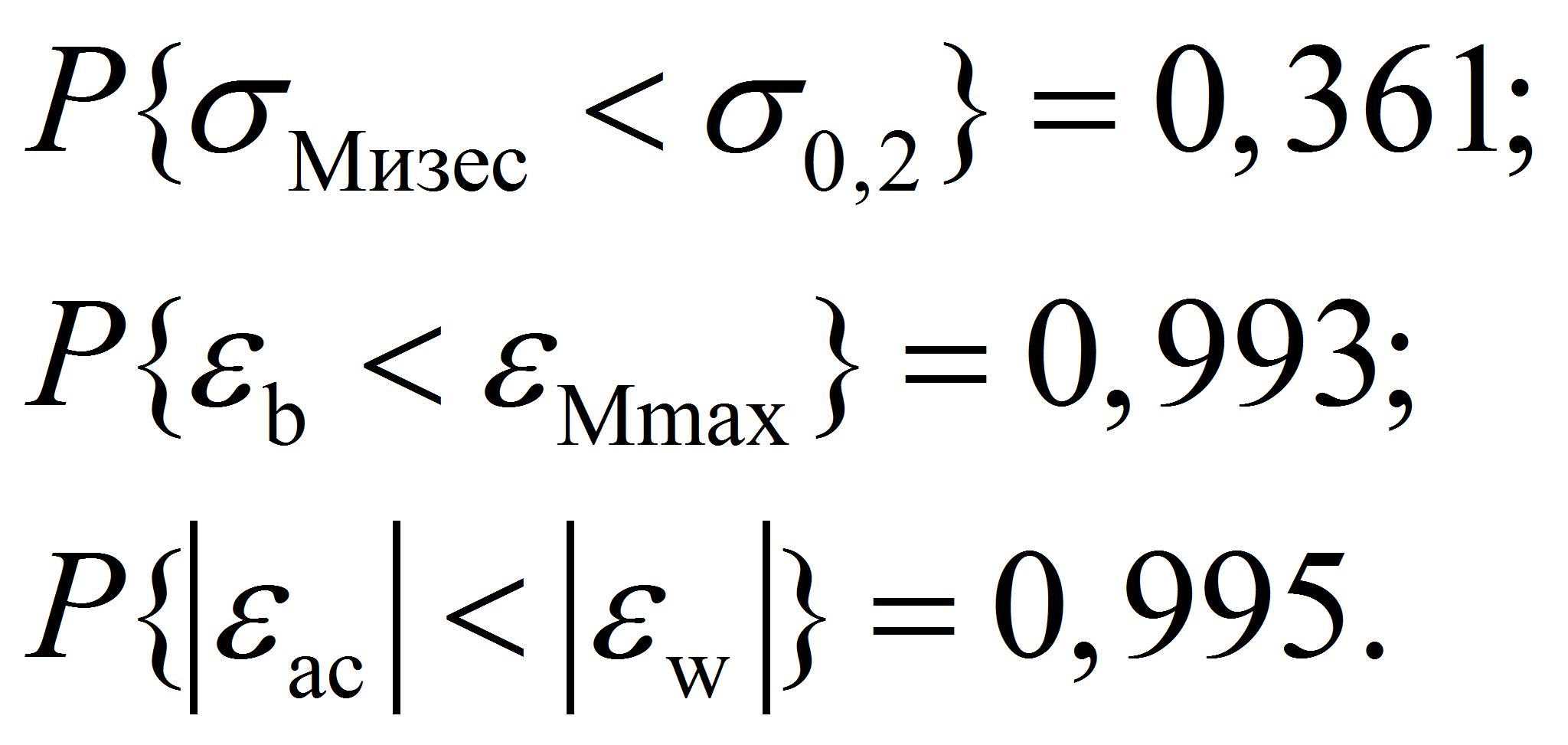
- Вызывающие аварийные ситуации природные воздействия (такие как землетрясения, ураганы, оползни, пучения и просадки грунта и т.д.) не поддаются контролю, и поэтому достаточный уровень безопасности по отношению к ним должен быть обеспечен на стадии проектирования. Следует отметить, что в расчетах на безопасность широко применяются вероятностные модели редких событий. Для оценки показателей безопасности и риска рассматриваемой конструкции воспользуемся теорией, предложенной В.В. Болотиным [5].
Рисунок 5 – Функция распределения напряжения &#;Мизес
Рисунок 6 – Функция распределения деформации εac
Рисунок 7 – Функция распределения деформации εb
-
- Таким образом, для рассматриваемых бугров пучения вероятность не наступления предельного состояния типа I составляет всего
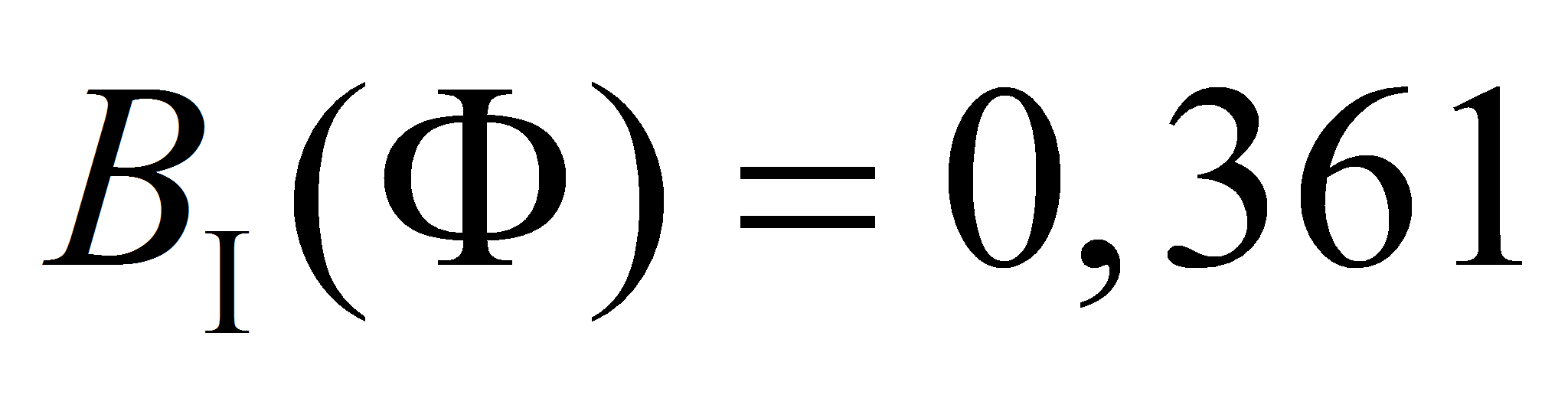 ,
а предельного состояния типа II –
,
а предельного состояния типа II –
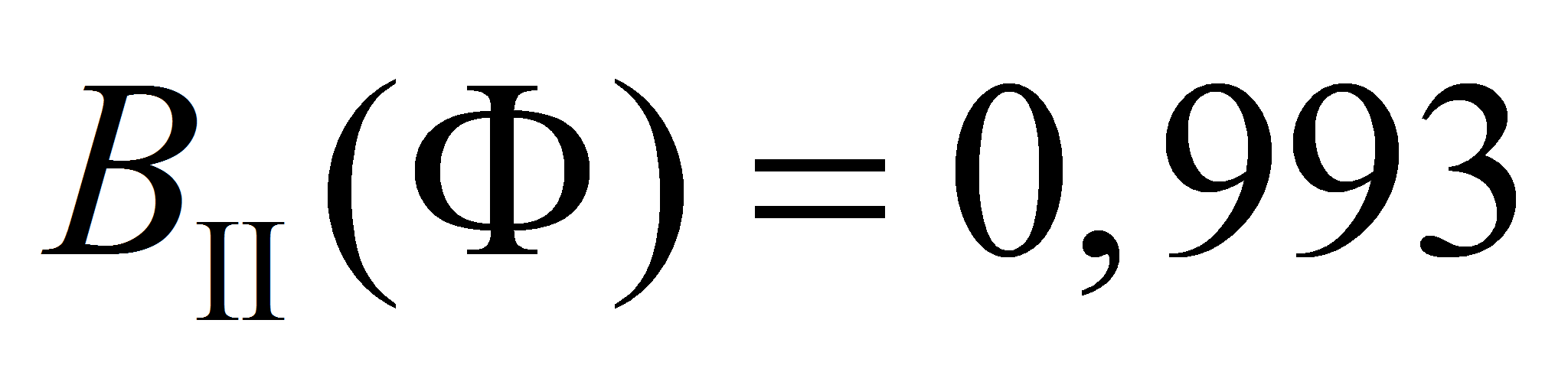 .
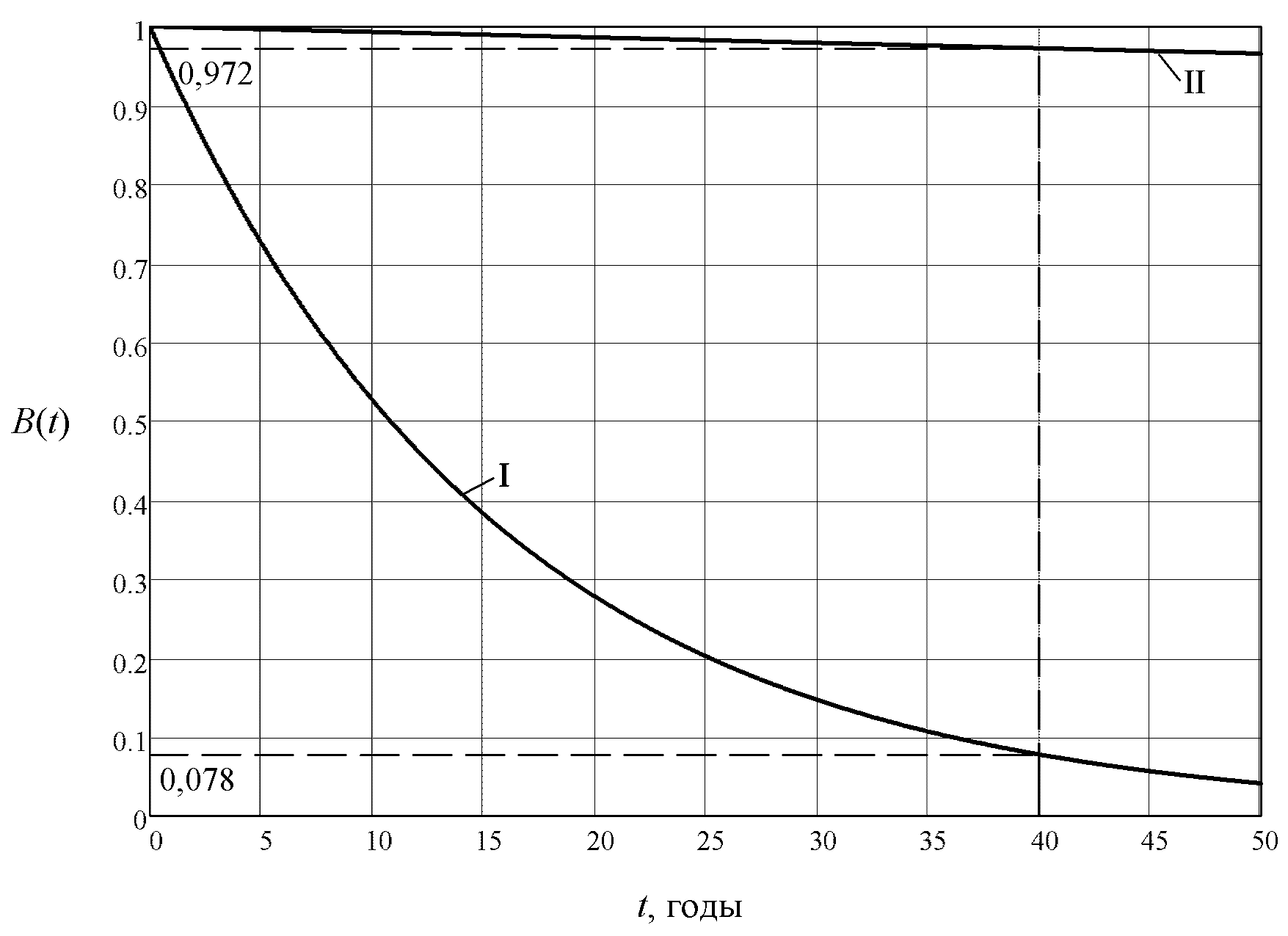
.- Вычисленные по формуле (7) функции полной безопасности приведены на рисунке 8. Как видно из графиков, например, для трубопровода со сроком службы T = 40 лет безопасность по критерию I составляет лишь 0,078, а по критерию II – безопасность равна 0,972.
- Таким образом, для рассматриваемых бугров пучения вероятность не наступления предельного состояния типа I составляет всего
Рисунок 8 – Функции безопасности
-
- Литература:
- Харионовский, В.В. Повышение прочности газопроводов в сложных условиях [Текст] / В.В. Харионовский. – Л.: Недра, 1990. – 180 с.
- Айнбиндер, А.Б. Расчет магистральных и промысловых трубопроводов на прочность и устойчивость: Справочное пособие [Текст] / А.Б. Айнбиндер. – М.: Недра, 1991. – 287 с.
Fault crossing analysis [Text] / Design Report N 5000-Y-36-10. – 2002. – 129 p.
- Методические рекомендации по расчётам конструктивной надёжности магистральных газопроводов: РД 51-4.2-003-97 [Текст]. – М.: ИРЦ Газпром, 1997. – 126 с.
- Болотин, В.В. Ресурс машин и конструкций [Текст] / В.В. Болотин. – М.: Машиностроение, 1990. – 448 с.