Кинематический и силовой анализ схемы зубчатого вариатора момента с не-симметричным дифференциалом

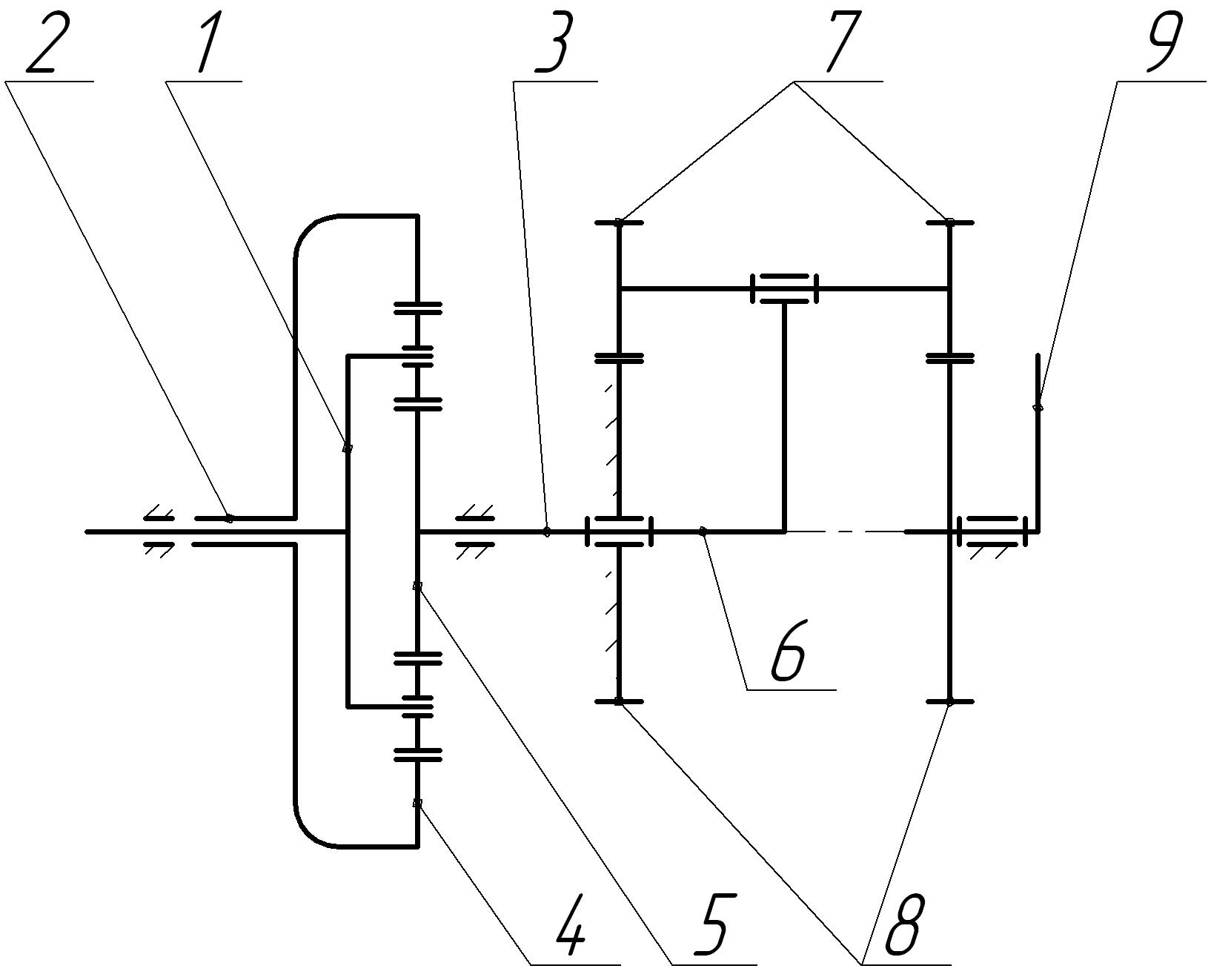
Кинематическая схема зубчатого вариатора момента с несимметричным дифференциалом представлена на рисунке 1.

Устройство состоит из дифференциального механизма, входным звеном которого является водило 1 с сателлитами и двумя центральными колесами 4 и 5, установленными на выходных валах 2 и 3 соответственно, один из которых соединен с водилом 6 планетарного механизма, который выполнен двухрядным, а на водиле 6 установлен с возможностью вращения блок сателлитов 7, образованный двумя соосными сателлитами с равным числом зубьев, взаимодействующими с двумя центральными соосными зубчатыми колесами 8, одно из которых закреплено неподвижно, а ко второму подвижному колесу жестко прикреплен рычаг управления 9 вариатором [1].

Рис. 1. Кинематическая схема зубчатого вариатора момента

Вариатор работает следующим образом. Вращение от двигателя подается на водило 1 дифференциала. Полученное водилом движение делится между выходными валами 2 и 3 с центральными колесами 4 и 5 соответственно. При неподвижном выходном вале 2 движение центрального колеса 5 передается на водило планетарного механизма 6, которое вместе с блоком сателлитов 7 свободно вращается вокруг центральных зубчатых колес 8, которые остаются неподвижными, поскольку одно из них закреплено неподвижно, а передаточное отношение равно бесконечности при равных числах зубьев центральных зубчатых колес 8. При приложении управляющего момента на рычаг управления 9 свободное движение водила 6 с блоком сателлитов 7 затормаживается, и возникающий момент торможения на валу водила 6 способствует возникновению крутящего момента на выходном валу 2 вариатора, причем этот момент пропорционален управляющему усилию. Угловая скорость выходного вала 2 также начинает увеличиваться по мере преодоления момента полезного сопротивления пропорционально управляющему воздействию.

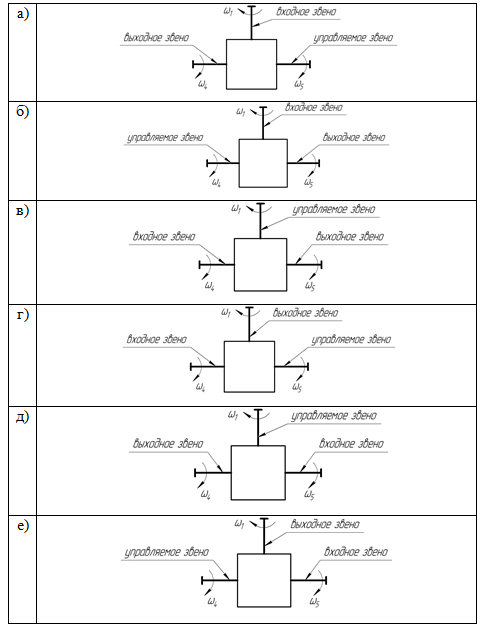
Рассмотрим кинематические и силовые параметры вариатора представленного на рисунке 1 в зависимости от того, какое из звеньев дифференциала будет ведущим, ведомым или управляемым (рисунок 2)

Рис. 2. Варианты расположения звеньев вариатора

Для определения угловых скоростей звеньев дифференциала используем формулу Виллиса [2, 3]:

. (1)

Передаточное отношение определяется через радиусы начальных окружностей зубчатых колес или через числа их зубьев

.

Обозначим величину (знак «-» так как центральные колеса при остановленном водиле вращаются в разные стороны) через р.

Тогда зависимость между моментами на центральных колесах (5 и 4) и водила (Н) без учета потерь на трение [2]:

;

или (2)

.

Используя формулы (1) и (2) определим кинематические и силовые зависимости вариатора.

Первый вариант (рисунок 2, а)

Водило 1 (Н) — входное звено, центральное колесо 5 соединено с нагружателем (управляющее звено), центральное колесо 4 соединено с ведомым валом (выходное звено).

При угловая скорость выходного звена будет иметь максимальное значение, которое составит

.

Таким образом, угловая скорость ведомого вала 4 изменяется в пределах

.

Силовые параметры выходного звена (крутящий момент и мощность ) без учета к. п.д. дифференциала связаны соотношениями

; .

Второй вариант (рисунок 2, б)

Водило 1 (Н) — входное звено, центральное колесо 5 выходное звено центральное колесо 4 соединено с нагружателем (управляющее звено).

При угловая скорость выходного звена будет иметь максимальное значение, которое составит

.

Таким образом, угловая скорость ведомого вала 5 изменяется в пределах

.

Силовые параметры выходного звена без учета к. п.д. дифференциала связаны соотношениями

; .

Третий вариант (рисунок 2, в)

Центральное колесо 4 — входное звено, центральное колесо 5 управляемое звено, а водило 1 (Н) выходное звено.

При угловая скорость выходного звена будет иметь максимальное значение, которое составит

.

Таким образом, угловая скорость выходного звена изменяется в пределах

.

Силовые параметры выходного звена без учета к. п.д. дифференциала связаны соотношениями

; .

Четвертый вариант (рисунок 2, г)

Центральное колесо 4 — входное звено, центральное колесо 5 выходное звено, а водило 1 (Н) управляемое звено.

При угловая скорость выходного звена будет иметь максимальное значение, которое составит

.

Таким образом, угловая скорость выходного звена изменяется в пределах

.

Силовые параметры выходного звена без учета к. п.д. дифференциала связаны соотношениями

; .

Пятый вариант (рисунок 2, д)

Центральное колесо 5 — входное звено, центральное колесо 4 управляемое звено, а водило 1 (Н) выходное звено.

При угловая скорость выходного звена будет иметь максимальное значение, которое составит

.

Таким образом, угловая скорость ведомого вала 4 изменяется в пределах

.

Силовые параметры выходного звена без учета к. п.д. дифференциала связаны соотношениями

; .

Шестой вариант (рисунок 2, е)

Центральное колесо 5 — входное звено, центральное колесо 4 выходное звено, а водило 1 (Н) управляемое звено.

При угловая скорость выходного звена будет иметь максимальное значение, которое составит

.

Таким образом, угловая скорость выходного звена изменяется в пределах

.

Силовые параметры выходного звена без учета к. п.д. дифференциала связаны соотношениями

; .

Проведенный кинематический и силовой анализ позволяет определить оптимальное расположение входного, выходного и управляемого звеньев зубчатого вариатора момента при использовании его в составе привода технологической машины, для максимально эффективной работы исполнительного органа при выполнении технологических операций.

Литература:

1. Пат. № 2445531 Российская федерация МПК F16H 3/74, F16H. Вариатор момента [Текст] / Кузнецов С. Н., Владимиров А. В., Лысянский В. А., Старченко И. Е.; заявитель и правообладатель Государственное образовательное учреждение высшего профессионального образования «Южно-Российский государственный университет экономики и сервиса» (ГОУ ВПО «ЮРГУЭС») — № 2010149799/11; заявл. 03.12.2010; опубл. 20.03.2012, Бюл. № 8.

2. Артоболевский И. И. Теория механизмов и машин [Текст] / И. И. Артоболевский. — М.: Наука, 1988. — 640 с.

3. Кирдяшев Ю. Н. Многопоточные передачи дифференциального типа [Текст] / Ю. Н. Кидряшев. — М.: машиностроение, 1981. — 231 с.