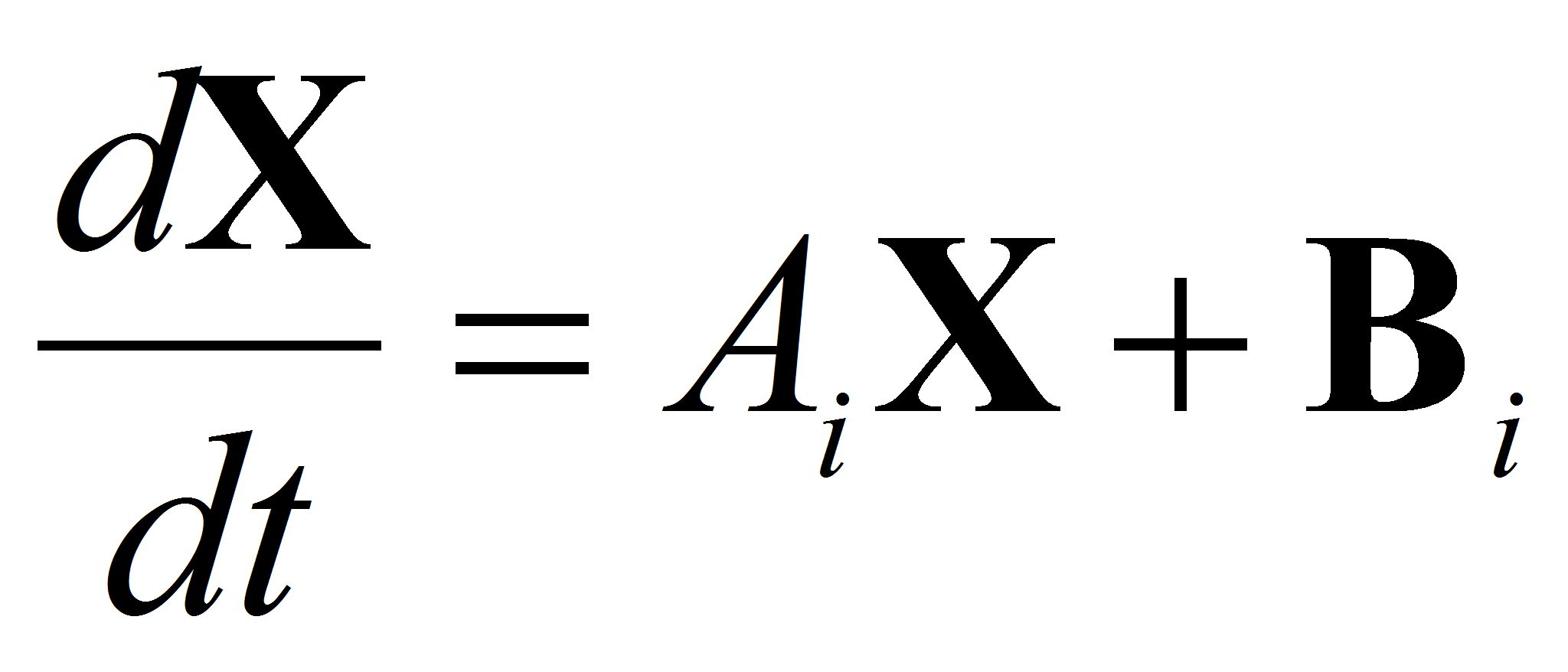Математическое моделирование импульсных преобразователей напряжения с нелинейной внешней характеристикой
Авторы: Андриянов Алексей Иванович, Краснов Никита Александрович
Рубрика: 4. Электротехника
Опубликовано в
II международная научная конференция «Актуальные вопросы технических наук» (Пермь, февраль 2013)
Статья просмотрена: 2188 раз
Библиографическое описание:
Андриянов, А. И. Математическое моделирование импульсных преобразователей напряжения с нелинейной внешней характеристикой / А. И. Андриянов, Н. А. Краснов. — Текст : непосредственный // Актуальные вопросы технических наук : материалы II Междунар. науч. конф. (г. Пермь, февраль 2013 г.). — Т. 0. — Пермь : Меркурий, 2013. — С. 28-31. — URL: https://moluch.ru/conf/tech/archive/73/3491/ (дата обращения: 24.04.2025).
На сегодняшний день накоплен достаточно большой практический опыт в области математического моделирования замкнутых систем с ШИМ, однако полностью универсальных подходов к моделированию различных по структуре преобразователей напряжения не существует, что требует создания новых математических моделей и алгоритмической базы для отдельно взятых топологий силовой части или их классов.
Рассмотрим математическую модель замкнутой системы управления с преобразователем напряжения первого рода с нелинейной внешней характеристикой. К преобразователям первого рода согласно [1] относятся непосредственный понижающий, мостовой, полумостовой преобразователи, преобразователь с выводом средней точки первичной обмотки трансформатора и д. р. Под нелинейной внешней характеристикой в данном случае понимается характеристика, обладающая как участком стабилизации напряжения, так и участком стабилизации тока. Такие преобразователи находят широкое применение в сварочных аппаратах инверторного типа и зарядных устройствах аккумуляторов [2].
Схема замещения преобразователя представлена на рис. 1. Здесь приняты следующие обозначения: E — напряжение источника питания; R — внутреннее сопротивление, характеризующее потери и преобразователе; L — индуктивность; C — емкость выходного конденсатора; Rн — сопротивление нагрузки; ИМ — импульсный модулятор; 1, 2 — коэффициенты передачи датчиков обратной связи выходного напряжения и тока дросселя соответственно; КУ — коммутирующее устройство контуров напряжения и тока; Uзu –напряжение задания; Uзi — задание на ток; ГРН — генератор развертывающих напряжений. При построении схемы замещения принимались во внимание допущения, представленные в [3].
Кусочно-гладкая модель системы автоматического управления на базе полупроводниковых преобразователей с широтно-импульсной модуляцией имеет вид
где Ai —
матрица постоянных коэффициентов на i-том
участке гладкости, Bi —
вектор вынуждающих воздействий на i-том
участке;![]() —
вектор переменных состояния.
—
вектор переменных состояния.
Рис. 1. Схема замещения замкнутой импульсной системы автоматического управления на основе понижающего преобразователя с нелинейной внешней характеристикой
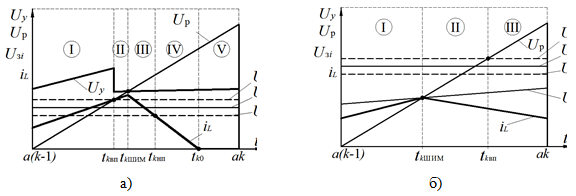
На рис. 2 представлены временные диаграммы, поясняющие особенности работы преобразователя на тактовом интервале. На рисунке приняты следующие обозначения: Uвп и Uнп — верхний и нижний пределы петли гистерезиса соответственно; Uр — развертывающее напряжение; iL — ток дросселя.
Рис. 2. К пояснению принципа действия силовой части преобразователя: а) tkвп<tkШИМ; б) tkШИМ>tkвп.
Как видно из рис. 2,а, на тактовом интервале в общем случае существует четыре информационные точки (моменты коммутации), когда схема меняет свою топологию: в момент tkШИМ напряжение управления после регулятора (Uу) сравнивается с развертывающим напряжением (Uр); в момент tkвп выходной сигнал датчика тока дросселя достигает значения верхнего предела гистерезиса (Uвп); в момент tkнп выходной сигнал датчика тока дросселя достигает значения нижнего предела гистерезиса (Uнп); в момент tk0 ток дросселя достигает нуля.
В зависимости от параметров системы возможны несколько режимов работы, каждый из которых связан с определенным порядком пересечения траекторией различных поверхностей сшивания участков гладкости в фазовом пространстве. На рис. 2 представлены два частных случая работы преобразователя.
Если tkвп<tkШИМ (достижение сигналом датчика тока верхнего порогового значения происходит раньше естественной коммутации ШИМ), на тактовом интервале происходит три коммутации (рис. 2, а):
первая коммутация происходит в момент tkвп. В данном случае преобразователь начинает работать в режиме обратной связи по току, т. е. на участке стабилизации тока. В этом случае коммутирующее устройства КУ на вход ШИМ-компаратора подает сигнал после регулятора α2, что приводит к резкому изменению сигнала управления;
вторая коммутация происходит в момент tkнп. После пересечения током дросселя нижнего порога гистерезиса преобразователь переходит в режим стабилизации напряжения;
третья коммутация происходит в момент tk0. Здесь ток дросселя падает до нуля (режим прерывистых токов).
Если tkвп>tkШИМ (рис. 2, б) на тактовом интервале происходит всего одна коммутация в момент tkШИМ. В данном случае преобразователь работает в режиме обратной связи по напряжению.
Таким образом, на тактовом интервале в общем случае существует пять участков гладкости (отмечены римскими цифрами на рис. 2, а). Решение дифференциального уравнения на каждом участке гладкости имеет вид
где а — период ШИМ, z —
относительное время на тактовом интервале, которое может быть
представлено как
![]() .
.
Анализ выражения показывает, что для вычисления вектора переменных состояния необходимо знать вектор X0 в начале участка и длительность самого участка. Переход от участка к участку осуществляется методом припасовывания, т. е. начальными условиями для каждого участка будет являться вектор переменных состояния в конце предыдущего участка.
Уравнения, определяющие моменты коммутации (разностные функции) могут быть представлены как
где Uвп и Uнп — верхний и нижний пороги гистерезиса соответственно; Uзu — задание на напряжение; Uрm — амплитуда развертывающего напряжения.
Поиск коэффициентов заполнения осуществляется путем решения
нелинейных трансцендентных уравнений:![]()
![]()
![]()
![]() ,
где zkШИМ,
zkвп,
zkнп,
zk0 —
моменты коммутации внутри такта в относительном времени
(коэффициенты заполнения).
,
где zkШИМ,
zkвп,
zkнп,
zk0 —
моменты коммутации внутри такта в относительном времени
(коэффициенты заполнения).
Полученная кусочно-гладкая математическая модель импульсного преобразователя, позволяет проводить бифуркационный анализ замкнутых импульсных систем с нелинейной внешней характеристикой.
Двухпараметрическая динамических карта режимов преобразователя представлена на рис. 3. На данной диаграмме приняты следующие обозначения: символом Пi,j обозначены параметрические области существования различных динамических режимов (индекс i — обозначает m-цикл, характерный для данной области, j — порядковый номер области на карте динамических режимов). Области П1,1 и П1,2 представляют собой область существования основного (m = 1) — проектного режима. Под проектным режимом понимается цикл периода один, когда частота колебаний выходного напряжения равна частоте ШИМ [4]. Работа преобразователя в данном режиме характеризуется высокими показателями качества преобразования энергии. Область, обозначенная П∞ соответствует недетерминированным режимам функционирования преобразователя (m →∞).
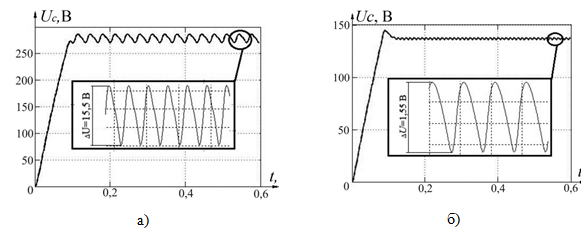
Карта на рис. 3 позволяет сделать выводы о существовании областей параметров, в которых реализуются непроектные режимы с m>1, обусловленными динамическими нелинейностями системы. Особое внимание следует уделить областям при малых значениях сопротивления нагрузки (П2,1, П3,1, П1,2). На рис. 4 (а, б) представлены временные диаграммы напряжения в областях П3,1 и П1,2. Как видно из рисунка, размах колебаний выходного напряжения в области П3,1 (рис. 4,а) в 10 раз больше размаха колебаний в области П1,2(рис. 4,б). Возникновение непроектных режимов при снижении сопротивления нагрузки до 50 Ом связано с достижением током нагрузки порогового значения, при котором начинается переход на участок стабилизации тока. При работе системы в области П3,1 происходит постоянного переключение коммутирующего устройства КУ, что приводит к возникновению сложной динамики.
Рис.3 Двухпараметрическая карта режимов работы преобразователя при параметрах системы: E = 1040 В, L = 0,01 Гн, C =10 мкФ, Rн = 40 Ом, 1 = 0,01, 2 = 1, Uзu = 4 В, Uзi = 7 А, Uрm = 10 В, α2 = 25.
При правильном выборе коэффициента усиления регулятора α1 (α1<1,5) система во всем диапазоне сопротивления нагрузки работает в проектном режиме (1-цикл) с малым коэффициентом пульсаций.
Рис. 4. Временные диаграммы выходного напряжения при α1=10: а) в области П3,1 при Rн=40 Ом; б) в области П1,2 при Rн=Ом.
Заключение.
Предлагаемая математическая модель может использоваться при бифуркационном анализе замкнутых систем с ШИМ, обладающих нелинейной внешней характеристикой. Использование разработанной математической модели в инженерном проектировании позволит на стадии технического проекта учитывать нелинейные динамические свойства системы, что не всегда возможно с использованием средств имитационного моделирования типа OrCAD и MatLab Simulink. Научно-обоснованный выбор параметров системы управления с использованием данной модели позволит исключить работу преобразователя в опасных режимах в процессе эксплуатации.
Литература:
Кобзев, А. В. Модуляционные источники питания РЭА / А. В. Кобзев, Г. Я. Михальченко, Н. М. Музыченко. — Томск: Радио и связь, 1990. — 336 с.
Мелешин, В. И. Транзисторная преобразовательная техника / В. И. Мелешин. — М.: Техносфера, 2005. — 627 с.
Болотовский Ю. И. OrCAD 9.x, OrCAD 10.x. Практика моделирования / Ю. И. Болотовский, Г. И. Таназлы, М.: СОЛОН-Пресс, 2008–207 с.
Кобзев. А. В. Нелинейная динамика полупроводниковых преобразователей / А. В. Кобзев, Г. Я. Михальченко, А. И. Андриянов, С. Г. Михальченко. — Томск: ТУСУР, 2007. — 224 с.
Анищенко, В. С. Нелинейная динамика хаотических и стохастических систем: Фундаментальные основы и избранные проблемы / В. С. Анищенко, Т. Е. Вадивасова, В. В. Астахов. — Саратов: Изд-во Саратов. ун-та, 1999. — 368 с.