Алгоритм получения матрицы жесткости четырехугольного конечного элемента
Авторы: Николаев Анатолий Петрович, Сорокина Елена Ивановна
Рубрика: 8. Строительство
Опубликовано в
II международная научная конференция «Современные тенденции технических наук» (Уфа, май 2013)
Статья просмотрена: 1188 раз
Библиографическое описание:
Николаев, А. П. Алгоритм получения матрицы жесткости четырехугольного конечного элемента / А. П. Николаев, Е. И. Сорокина. — Текст : непосредственный // Современные тенденции технических наук : материалы II Междунар. науч. конф. (г. Уфа, май 2013 г.). — Т. 0. — Уфа : Лето, 2013. — С. 53-56. — URL: https://moluch.ru/conf/tech/archive/74/3809/ (дата обращения: 16.11.2024).
В статье исследуются в трех вариантах алгоритмы получения матриц жесткости четырехугольного конечного элемента.
Ключевые слова: объемный конечный элемент, матрица жесткости, вектор узловых неизвестных.
Для расчета осесимметрично нагруженных тел вращения из несжимаемых материалов разработаны объемные конечные элементы с поперечным сечением в виде четырехугольника. Для выполнения численного интегрирования произвольный четырехугольник в системе координат r, z с узлами i, j, k, l отображался на квадрат с локальными координатами ξ, η, изменяющимися в пределах -1 ≤ ξ, η ≤ 1. Зависимость между координатами r, z и локальными координатами ξ, η определялась билинейными соотношениями
; 
, (1)
где 
— матрицы-строки координат узлов четырехугольника.
Дифференцированием соотношений (1) определялись производные глобальных координат r,ξ, r,η, z,ξ, z,η и локальных координат ξ,r, η,r, ξ,z, η,z в глобальной системе координат.
Четырехугольный конечный элемент разрабатывался в трех вариантах.
1. Столбец узловых неизвестных содержит только перемещения и принимается в виде
; (2)
где
— перемещения вдоль осей r и z соответственно в узловой точке m (m = i, j, k, Каждая составляющая перемещения внутренней точки конечного элемента аппроксимируется через узловые неизвестные билинейными зависимостями (1).
Вектор-столбец внутренней точки конечного элемента 
определяется в матричном виде выражением
, (3)
где матрица [A] имеет вид
.
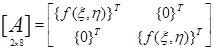Деформации внутренней точки конечного элемента определяются матричным выражением
. (4)
Гидростатическое давление σ0 принимается постоянным по площади четырехугольника.
2. Во втором варианте конечного элемента в каждом его узле в качестве узловых неизвестных принимаются перемещения и их первые производные. Вектор узловых неизвестных в локальной системе координат имеет вид
, (5)
где
;
;
— производные радиального и осевого перемещений в локальной системе координат.
Перемещения внутренней точки конечного элемента определяются через векторы узловых перемещений в локальной системе координат соотношениями
;
, (6)
где компонентами матрицы 
, содержащей функции формы, являются полиномы Эрмита третьей степени.
С использованием аппроксимирующих соотношений (6) формируется матричная зависимость (3) и (4).
Гидростатическое давление принимается постоянным по площади четырехугольника.
3. В третьем варианте конечного элемента перемещения аппроксимировались соотношениями второго варианта, а гидростатическое давление считалось изменяющимся в зависимости от узловых значений по билинейному закону
, (7)
где
.
Для получения матрицы жесткости и векторов узловых усилий дискретных элементов при действии сил, распределенных по объему, используется равенство работ внешних и внутренних сил на возможных перемещениях
v
, (8)
где
— элементарный объем дискретного элемента;
— вектор-строка составляющих поверхности сил.
С использованием матричной зависимости
, (9)
равенство (8) принимает вид
, (10)
где
ds — элементарная площадка поперечного сечения элемента.
Объемная деформация ε0, входящая в (15), определяется выражением
. (11)
Принимая во внимание (3), (4), (9), (10) и (11) выражение (12) представим в виде
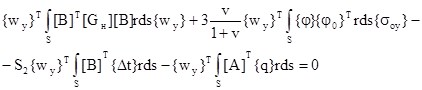(13)
Выполняя минимизацию функционала (13) по компонентам вектора 
и по компонентам узловых неизвестных гидростатического давления 
, получим систему уравнений
;
, (14)
где
;
;
.
Систему (14) можно представить в традиционной конечно-элементной формулировке
, (15)
где
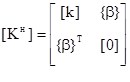— модифицированная матрица жесткости конечного элемента;
— вектор узловых сил конечного элемента.
— вектор узловых неизвестных конечного элемента.
При получении матриц жесткости в первом и втором вариантах конечных элементов матрица [β] соотношения (14) представляет собой столбец {β}.
Модифицированная матрица жесткости [Кн] имеет размеры 9×9 — в первом варианте конечного элемента, 25×25 — во втором варианте и 28×28 — в третьем варианте.
В качестве примера определено напряженно-деформированное состояние защемленной по торцам цилиндрической оболочки, нагруженной внутренним давление интенсивности q=
, при следующих исходных данных: внутренний радиус R=0,5 м; толщина стенки оболочки h=0,05 м; модуль упругости материала Е = 2 · 105
; коэффициент Пуассона υ = 0,5. расчет выполнялся в трех вариантах.
В первом варианте использовался конечный элемент с узловыми неизвестными в виде радиального и осевого перемещения υ. Гидростатическое давление σ0 принималось постоянным по площади четырехугольника.
Во втором варианте расчет выполнен с использованием конечного элемента, узловыми неизвестными которого являлись перемещения и их первые производные. Гидростатическое давление σ0 принималось постоянным по площади сечения объемного конечного элемента.
В третьем варианте расчета использовался элемент с узловыми неизвестными в виде перемещений и их первых производных. Гидростатическое давление распределялось в поперечном сечении объемного конечного элемента по линейному закону.
Анализ результатов показал хорошую сходимость вычислительного процесса и совпадение результатов по вариантам.
Сравнительными расчетами установлено, что наилучшие результаты получаются при использовании конечного элемента с узловыми неизвестными в виде перемещений и их первых производных, а также гидростатических давлений (т. е. в третьем варианте).
