Управление движением вращающегося тела с полостью, частично заполненной идеальной жидкостью

Рассматривается в линейной постановке задача Коши для возмущённого относительно равномерного вращения движения динамически симметричного твёрдого тела с полостью, содержащей идеальную жидкость со свободной поверхностью. При этом никаких ограничений на форму полости и характер возмущённого движения не накладывается. На основе полученных уравнений исследуется устойчивость стационарного вращения тела с жидкостью и намечается постановка широкого класса задач оптимального управления, для которых используются классические подходы принципа максимума Понтрягина и принципа оптимальности Беллмана.

Ключевые слова: уравнения Навье-Стокса, принцип максимума Понтрягина, вихревые движения жидкости

В работе проводится анализ возмущённого относительно равномерного вращения всей системы как твёрдого тела с полостью, частично заполненной идеальной жидкостью. На основе полученных уравнений исследуется устойчивость свободного вращения тела с жидкостью. Найденная более сложная чем в [1,2] зависимость угловых скоростей от моментов позволяет ставить различные задачи оптимального управления. После преобразований устанавливается применимость формализма Гамильтона-Понтрягина, как и в [1–3].

Постановка задачи

Здесь используются результаты [4, 5, 7]. Рассмотрим твердое тело с полостью D, частично заполненной идеальной несжимаемой жидкостью плотности ρ, частично газом, давление которого , движущееся в поле массовых сил с потенциалом U. Область Q, занятая жидкостью, ограничена смоченной поверхностью S полости и свободной поверхностью . Уравнения движения жидкости, граничные и начальные условия запишем в произвольной системе координат , жестко связанной с твердым телом:

    .                                                (1)

Точкой обозначена производная по времени в системе координат ;  — абсолютное ускорение точки O,  — абсолютная угловая скорость тела,  — его угловое ускорение,  — радиус–вектор, отсчитанный от точки O,  — скорость жидкости в системе координат , t — время, P — давление,  — орт внешней нормали к ,  — уравнение свободной поверхности жидкости. Кинетический момент  тела с жидкостью относительно центра инерции  всей системы запишем в виде

                                                                                                  (2)

Здесь J — тензор инерции всей системы относительно точки , складывающийся из тензоров инерции тела  и затвердевшей жидкости  относительно той же точки. Область  ограничена смоченной поверхностью  и свободной поверхностью  в невозмущенном движении, которая в первом приближении имеет цилиндрическую форму. В рассматриваемом приближении тело с полостью, содержащей жидкость, является гиростатом — центр инерции системы  неподвижен относительно системы координат  [6], а тензоры , , J постоянны в этой системе координат. Второе слагаемое в равенстве (2), называемое гиростатическим моментом, не зависит от выбора полюса и может быть подсчитано относительно точки , что и сделано в равенстве (2). Уравнение моментов относительно точки  запишем в системе координат , связанной с телом

                                                                                                            (3)

Здесь  — главный момент относительно точки  всех внешних сил, действующих на тело с жидкостью. Уравнения (1) — (3) вместе с обычными уравнениями движения центра инерции, кинематическими соотношениями и начальными условиями полностью описывают динамику тела с жидкостью. Пусть невозмущенное движение тела с жидкостью относительно центра инерции  представляет собой вращение всей системы вокруг оси , проходящей через точку  параллельно оси , с постоянной угловой скоростью  так, что свободная поверхность имеет цилиндрическую форму. В невозмущенном движении имеем: , , , , где  — орт оси ,  — радиус свободной поверхности в невозмущенном движении, , , . Рассмотрим возмущенное движение системы. Положим

 , ,                                                                                              (4)

и будем считать в возмущенном движении величины  малыми первого порядка. Подставляя соотношения (4) в уравнения (1) и отбрасывая малые высших порядков, приведем задачу о движении жидкости к виду

,    .                                                                               (5)

Аналогично уравнения движения тела с жидкостью примут вид . Рассмотрим гидродинами-ческую задачу (5). Положим в задаче (5)  и рассмотрим вспомогательную задачу о колебаниях жидкости в равномерно вращающемся сосуде, решение которой будем искать в форме гармонических колебаний Таким образом, имеем следующую задачу:    . Воспользуемся линейным преобразованием  [7]: . Тогда для функции  получаем краевую задачу на собственные значения

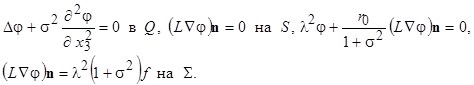                (6)

Устойчивость динамической системы «тело — жидкость»

Рассмотрим вопрос об устойчивости свободного вращения описанной системы. В пространстве Лапласа характеристическое уравнение системы (11) при  имеет вид (при )

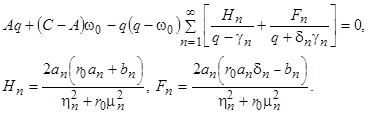                                           (7)

Для устойчивости стационарного вращения необходимо, чтобы все корни уравнения (7) были действительными. Ограничимся первым приближением, оставив вместо бесконечной суммы в (7) один главный член (). В этом случае характеристическое уравнение является многочленом третьей степени относительно q:

                                                                                               (8)

Здесь

Заменяя в уравнении (8) неизвестное q новым неизвестным , связанным с q равенством  получим неполное кубическое уравнение относительно :  где  Для устойчивости свободного вращения параметры системы должны удовлетворять условию  При этом на границе области устойчивости выполняется условие .

Возмущение как функция управляющего момента.

Для решения задачи оптимального управления вращением системы тело — жидкость необходимо иметь выражение возмущения угловой скорости  как функции управляющего момента .

Для дальнейшего анализа оставим одно слагаемое в бесконечной сумме в первом уравнении системы (7).

Преобразование оригинала  по Лапласу будем обозначать , т. е.

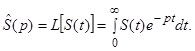
Выполнив преобразование Лапласа, выразим  из второго и третьего уравнений и, подставив в первое уравнение, получим выражение  в пространстве Лапласа:

                                          

Для обратного преобразования Лапласа воспользуемся теоремой о свертке и теоремами разложения операционного исчисления [6]. Тогда

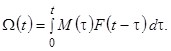                                                                                            (9)

Задача управления возмущенным движением

Вспомним, что , . Введем следующие обозначения:

                                               

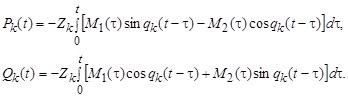
Тогда имеем

, .                                                                                             (10)

Окончательно получаем эквивалентную систему обыкновенных дифференциальных уравнений, которую вместе с начальными условиями, введя обозначения

 

запишем в виде

                                                                                              

Заключение

В работе рассмотрено возмущенное относительно равномерного вращения движение тела с полостью, содержащей идеальную жидкость со свободной поверхностью. Задача исследована в линейной постановке. Это означает, что угловые скорости, перпендикулярные основному вращению, много меньше угловой скорости основного вращения. Это достигается выбором времени в функционалах оптимизации, либо искусственным поддержанием достаточно большой угловой скорости продольного вращения. Проблема совместного решения уравнений гидродинамики и механики сведена к решению некоторой задачи на собственные значения. Происходящее при этом отделение временной координаты от пространственных координат позволило авторам анализировать произвольное возмущенное движение тела, а решение краевых задач находить для полостей произвольной формы. Методом возмущений решена задача об устойчивости свободного вращения тела с жидкостью. Ставится широкий класс задач оптимального управления, для которых применим формализм Гамильтона — Понтрягина.

Литература:

1.         Гурченков А. А., Есенков А. С., Цурков В. И. Управление движением ротора с полостью, содержащей идеальную жидкость ч.1 // Изв РАН. ТСУ. 2006. № 1. С. 135–142.

2.         Гурченков А. А., Есенков А. С., Цурков В. И. Управление движением ротора с полостью, содержащей идеальную жидкость ч.2 // Изв РАН. ТСУ. 2006. № 3. С. 82–89.

3.         Гурченков А. А., Есенков А. С., Цурков В. И. Управление движением ротора с полостью, содержащей вязкую жидкость // АиТ. 2007. № 2. С. 81–94.

4.         Гурченков А. А., Корнеев В. В. Носов М. В. Динамика слабовозмущенного движения заполненного жидкостью гироскопа и задача управления // ПММ, 2008. Т. 72. Вып. 6. С. 904–911.

5.         Гурченков А. А. Динамика завихренной жидкости в полости вращающегося тела. М.: Физматлит, 2010.

6.         Диткин В. А., Прудников А. П. Интегральные преобразования и операционное исчисление. М.: Наука, 1974.

7.         Гурченков А. А., Грдина Е. Д., Башлыков А. М. Задача о колебаниях ротора, содержащего жидкость со свободной поверхностью // ЖВМиМФ. 2002. V.42. N.1. P.101–105.

---