Получение оверлеев векторных данных большого объёма

Рассмотрена задача построения оверлеев (пересечения, объединения, разности) векторных данных, содержащих большое число контуров простой структуры. С целью решения этой задачи изучены представленные в литературе методы. Как оказалось, лишь три метода из множества имеющихся могут претендовать на решение этой задачи за разумное время. При более детальной изучении и тестировании имеющихся реализаций этих методов лишь одна из них (Vatti/GPC) оказалась пригодной, причём только после внесения существенных доработок. Итоговая улучшенная реализация алгоритма апробирована на массиве данных по пожарам и пригодна для решения практически важных задач.

Ключевые слова: оверлеи многоугольников, скан-линейный алгоритм, шейпфайл.

Введение

В различных приложениях, связанных с обработкой данных дистанционного зондирования Земли (ДЗЗ), появляется задача вычисления объединения, пересечения, разности множеств, представляющих собой площади земной поверхности, заданные в векторном виде, а именно как набор замкнутых многоугольников, описанных последовательностями вершин [1]. Типичными задачами являются: объединение площадей, полученных при обработке данных последовательных пролётов спутников над заданным участком; получение пересечения такой объединённой площади (имеющей обычно весьма сложную форму) с границами административных образований или областями определённого типа растительности; вычисление разности двух областей с целью определения добавленных участков.

Постановка задачи

Области (называемые также операндами) состоят каждая из многих (до десятков тысяч) контуров:

, , .

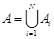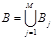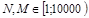Каждый контур является многоугольником (полигоном) и представлен последовательностью своих вершин, число вершин обычно невелико (порядка десяти), но может достигать нескольких тысяч:

, .

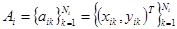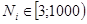Контуры невырожденные, не имеют самопересечений, однако контуры одного аргумента могут взаимно пересекаться. Общее число точек во всех контурах может достигать сотен тысяч:

.

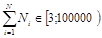Требуется построить алгоритмы, вычисляющие объединение 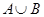, пересечение 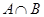, разность  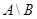таких множеств.

Подобные задачи решались многими исследователями при помощи различных методов. В [4] проводится обзор алгоритмов, предложенных Sutherland, O'Rourke, Weiler, Леонов, Schutte, Holwerda, Margalit и сравнение их по ряду таких параметров, как вычислительная устойчивость, ресурсоёмкость, скорость работы, простота программной реализации. Кроме этого, авторами рассматривались также алгоритмы Liang-Barsky, Maillot, Vatti, Greiner-Horman, рекомендованные в [5]. Однако, несмотря на кажущееся обилие методов, большая часть из них оказалась непригодной из-за большой размерности задачи. Многие из перечисленных методов рассчитаны на работу с очень сложными, но малочисленными контурами, в то время как здесь имеется прямо противоположная ситуация: большое число относительно простых контуров.

Алгоритмы Сазерленда, О'Рурка, Шутте, Лианга-Барского и Maillot признаны непригодными, так как требуют отсутствия «дыр» и/или выпуклости хотя бы одного из операндов. Алгоритм Вейлера-Азертона пригоден для операции лишь с двумя (пусть и очень сложными) контурами, а алгоритм Маргалита-Кнотта пригоден лишь в случае когда один из операндов представлен единственным многоугольником. Поскольку число многоугольников может составлять десятки тысяч (хоть и очень простых), для операций в нашем случае потребуются десятки тысяч вызовов этих алгоритмов с последующим объединением результатов; причём оптимальное объединение результатов само по себе является непростой задачей. Алгоритм Холверда является предшественником более быстрого и стабильного алгоритма Ватти, а алгоритм Леонова — модификацией алгоритма Грейнера-Хормана. Таким образом, более подробному разбору, в том числе экспериментальной проверке, подверглись три алгоритма: триангуляции [3], Леонова [2] и Ватти [9].

Анализ трёх алгоритмов

Триангуляцией многоугольника называется его представление в виде полного набора взаимно не пересекающихся треугольников. Основная идея алгоритма построения оверлеев (т. е. пересечения, объединения или разности) многоугольников с помощью триангуляции заключается в построении совместной триангуляции исходных многоугольников (при которой структурными линиями служат стороны обоих аргументов), а затем выбора из множества полученных треугольников некоторых, согласно выполняемой операции и принадлежности каждого из треугольников исходным множествам-аргументам. Избранные треугольники можно наконец объединить в многоугольники, хотя для рассматриваемой задачи это не обязательно.

Алгоритм Леонова (Грейнера-Хормана) состоит в поиске и маркировке всех пар пересекающихся рёбер, после чего проводится трассировка, начинающаяся с любой вершины одного из контуров, выделяющая все минимальные ограничивающие контуры областей, полученных наложением аргументов. Каждый из контуров маркируется согласно выполняемой операции и принадлежности аргументам, после чего проводится сборка этих контуров в результирующее множество.

Алгоритм Ватти также называется скан-линейным. Его основная идея состоит в том, что все вершины аргументов упорядочиваются по значению их ординат, и каждая из них порождает горизонтальную скан-линию. Далее при последовательном просмотре скан-линий производится анализ их пересечений с точками и рёбрами аргументов, поддерживается список контуров, в который вносятся изменения, соответствующие характеру и последовательности пересечения очередной скан-линии с вершинами и сторонами.

Поскольку все эти алгоритмы достаточно сложны, в качестве основы были взяты программные реализации, разработанные ранее. Для построения триангуляции и для выполнения операций над треугольниками были использованы алгоритмы из библиотеки Computational Geometry Algorithms Library [6]. Алгоритм Леонова был взят из [7]. За основу реализации алгоритма Ватти был взят код [8].

Для первого этапа тестов были использованы данные о пожарах, полученные в 2011 году. Было использовано 3906 векторных файлов, каждый из которых содержит от одного до нескольких тысяч полигонов простой формы (обычно это четырёхугольники), являющихся фактически векторным представлением пикселей растрового изображения, на которых детектирован пожар. Файлы были разбиты на группы по месяцам. Для тестов алгоритмов на первом этапе была использована подгруппа файлов, имеющих общий размер 100 килобайт. Также была сформирована группа, включающая в себя все файлы всех месяцев. В Таблице 1 приводятся характеристики этих групп.

Таблица 1

Характеристики тестовых групп шейпфайлов

Тесты всех трёх алгоритмов проводились только для «Подгруппы», результаты представлены в Таблице 2.

Таблица 2

Результаты обработки тестовой подгруппы файлов тремя выбранными алгоритмами

Имеющаяся реализация алгоритма Леонова не прошла по временнЫм ограничениям, кроме того, в этой реализации при вычислениях производится перевод координат из чисел с плавающей точкой в целочисленные 64-битные значения и обратно. По этой причине координаты точек не сохраняются строго, что может вызвать проблемы при дальнейшей обработке. По этим причинам было принято решение отказаться от алгоритма Леонова.

Что касается триангуляционного алгоритма, то при переходе к расчётам на реальных данных (после вполне благополучных тестов на «Подгруппе») обнаружился его существенный недостаток. На реальных данных один и тот же пожар может быть детектирован десятки раз. Соответственно, десятки файлов содержат контур пожара в одном и том же месте. На Рис.1. приводится пример объединения двух прямоугольных контуров (каждый из которых может быть представлен как два треугольника), в результате которого при использовании метода триангуляции получается 10 треугольников, и объединение трёх контуров, в результате которого получается уже 31 треугольник.

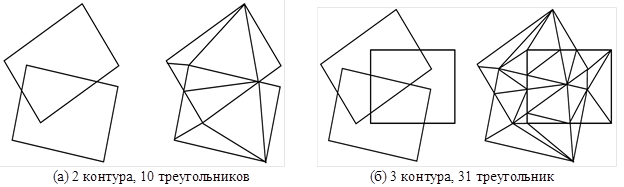
Рис. 1. Пример нарастания сложности триангуляции

В общем случае при объединении наложенных контуров количество треугольников растёт квадратично от числа объединений. Таким образом, на реальных данных, содержащих области с многократным перекрытием число треугольников резко возрастает, а сами они уменьшаются до ничтожных площадей. Обратное объединение треугольников в некоторую фигуру само по себе является трудной задачей, требующей существенной доработки алгоритма триангуляции. По этой причине было принято решение отказаться от метода триангуляции.

Доработки алгоритма Ватти

За основу реализации алгоритма Ватти был взята библиотека оверлеев [GPC]. Оригинальный код этой библиотеки оказался непригоден для решения в полном объёме задач, поставленных в проекте, и был переработан. были сделаны следующие существенные доработки: исключена рекурсия при перемещении по спискам (деревьям) вершин, активных рёбер, фигур; исключено задание в явном виде таблицы попарных пересечений многогранников; учтена возможность пересечения фигур, находящихся в одном файле. Опишем каждую из этих доработок более подробно.

Рекурсия при перемещении по спискам

Алгоритм Ватти оперирует с несколькими списками объектов, это список вершин (составляемый из вершин исходных фигур, пополняется в процессе работы пересечениями рёбер), список активных рёбер, списки активных фигур и построенных фигур. В версии GPC эти списки реализованы как бинарные деревья, для оптимизации поиска. Однако, перемещение по спискам в исходном коде было реализовано в виде рекурсивного вызова функций обработки элемента. При работе с большими объёмами данных степени самых удалённых от корня вершин деревьев возрастают до нескольких десятков тысяч. При использовании рекурсивных вызовов для перемещения по дереву это означает вызов функции самой из себя несколько десятков тысяч раз. По этой причине при обработке больших групп файлов (например «Май» и «Июнь») происходило исчерпание стека вызовов и аварийное завершение алгоритма и самой программы.

Были сделаны доработки с целью исключить рекурсию. В переработанной версии алгоритма глубина вызовов функций не превышает 5, рекурсия исключена.

Таблица попарных пересечений

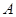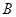В исходной версии алгоритма для минимизации вычислений алгоритма применён простой метод уменьшения количества контуров, для которых используется скан-линейный метод. Идея заключается в том, что каждый из аргументов  и представлен множеством отдельных контуров, но при этом далеко не каждый контур  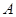пересекает хотя бы один контур 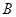и наоборот. Таким образом каждый операнд можно разбить на два подмножества, активное и пассивное:

, .

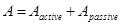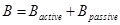Пассивные части операндов исключаются из выполнения скан-линейной процедуры и могут быть добавлены уже потом к результату:

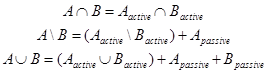
Однако, реализация этого подхода выполнена, очевидно, с расчётом на небольшое количество контуров. В частности, для получения списков пассивных и активных контуров используется массив чисел, имеющий размер, равный произведению числа контуров двух операндов. Для решаемых в рамках проекта задач оба эти числа могут превышать 100000, что приводит к невозможности размещения в оперативной памяти такого массива.

Была произведена доработка алгоритма, в результате которой необходимый размер массива стал равен не произведению, а сумме числа контуров в операндах.

Пересечение фигур в одном шейпфайле

Проверка условий включения каждого полученного многогранника в результат осуществляется подсчётом числа пересечений скан-линии с рёбрами многоугольников 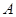 и 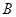. С этим связана особенность алгоритма, которая потребовала дополнительных усилий для его использования, а именно, при наличии пересекающихся фигур в каком-либо операнде (например 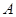, т. е. 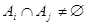) алгоритм исключает их пересечение из результата. Пример на рисунке ниже.

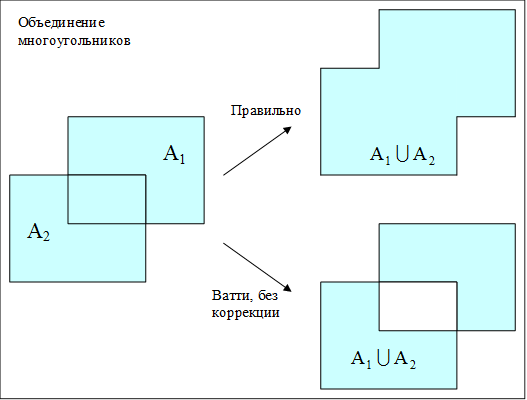
Рис. 2. Пример работы алгоритма Ватти при условии наличия пересекающихся фигур в одном операнде

Была сделана надстройка над алгоритмом. Каждый из операндов (пусть это будет 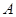) предварительно разбивался на группы контуров (далее такая группа называется слоем), такие, что внутри каждой такой группы контуры не пересекались: 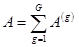, , 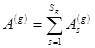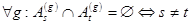. Далее слои  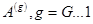последовательно объединяются.

Для разбиения на слои разработан специальный алгоритм, использующий проецирование фигур (точнее, их ограничивающих прямоугольников) на вспомогательный растр. Работа алгоритма представлена блок-схемой на Рис.3. В результате исполнения алгоритма получается несколько слоёв, в каждом из которых содержатся взаимно непересекающиеся контуры. Как правило, слои с большим порядковым номером содержат меньшее количество контуров. Поэтому слои объединяются начиная с меньших номеров, с целью уменьшения количества вычислений алгоритмом Ватти.

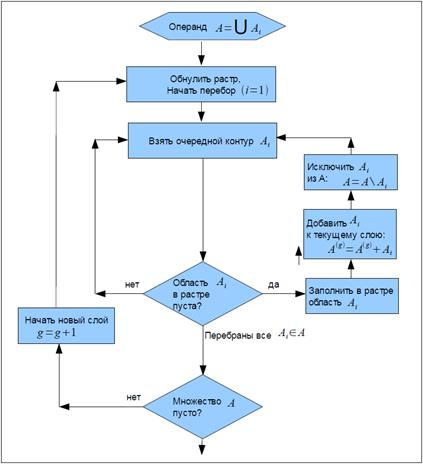
Рис. 3. Алгоритм разбиения на слои

Результаты тестов

Результаты тестов алгоритма на множествах Таблицы 1 приведены в Таблице 3. Проводилась операция объединения всех контуров всех файлов в группе в один набор контуров.

Таблица 3

Результаты тестов алгоритма Ватти

Заключение

В целях автоматизации построения оверлеев при обработке данных дистанционного зондирования Земли были изучены имеющиеся методы и их программные реализации. Лишь один из имеющихся методов оказался по сути пригоден для решения поставленных задач, причём только после значительных доработок. Сделано несколько доработок программной реализации алгоритма, позволивших существенно расширить область его применимости и размерность обрабатываемых им данных. Сделана надстройка над алгоритмом, позволяющая обойти один из его принципиальных недостатков, некорректную обработку аргументов со взаимно пересекающимися контурами. Полученный в итоге алгоритм пригоден для решения практических задач и используется в этом качестве.

В процессе работы выяснились следующие недостатки. Имеющаяся реализация алгоритма Ватти обладает алгоритмической сложностью 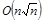, где 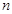 — сумма числа точек аргументов. Алгоритм Ватти может быть доработан для оптимизации поиска пересечений рёбер таким образом, что его сложность станет .

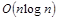Литература:

1.                                  Бондур В. Г. Актуальность и необходимость космического мониторинга природных пожаров // Вестник ОНЗ РАН. 2010. Том 2. NZ11001.

2.                                  Леонов М. В., Никитин А. Г. Эффективный алгоритм, реализующий замкнутый набор булевых операций над множествами многоугольников на плоскости / Препринт Института систем информатики СО РАН № 46. 1997. 20 с. // http://www.iis.nsk.su/files/preprints/046.pdf

3.                                  Скворцов А. В. Триангуляция Делоне и ее применение. Томск: Изд-во Томского ун-та, 2002.-128 с.

4.                                  Ченцов О. В., Скворцов А. В. Обзор алгоритмов построения оверлеев многоугольников // www.ict.edu.ru/ft/004461/46.pdf

5.                                  Agoston M. K. Computer Graphics and Geometric Modeling // Springer. 2004. 920 p.

6.                                  Computational Geometry Algorithms Library // http://www.cgal.org/

7.                                  Leonov M. PolyBoolean // http://www.complex-a5.ru/polyboolean/comp.html

8.                                  Murta A. General Polygon Clipper Library // http://www.cs.man.ac.uk/~toby/gpc/

9.                                  Vatti B. R. A generic solution to polygon clipping // Communications of the ACM. 1992. V.35. N.7. P.56–63.