Исследование методов реконструкции трехмерных моделей манекенов
Автор: Грудинин Сергей Николаевич
Рубрика: 1. Информатика и кибернетика
Опубликовано в
Дата публикации: 04.04.2014
Статья просмотрена: 1344 раза
Библиографическое описание:
Грудинин, С. Н. Исследование методов реконструкции трехмерных моделей манекенов / С. Н. Грудинин. — Текст : непосредственный // Технические науки: проблемы и перспективы : материалы II Междунар. науч. конф. (г. Санкт-Петербург, апрель 2014 г.). — Т. 0. — Санкт-Петербург : Заневская площадь, 2014. — С. 5-9. — URL: https://moluch.ru/conf/tech/archive/89/5486/ (дата обращения: 24.04.2025).
В работе рассматривается метод реконструкции базовой модели из полигональной модели, полученной трехмерным сканированием для целей параметрического моделирования виртуальных манекенов. На сегодняшний день существует три основных группы методов поверхностного моделирования трехмерных форм человеческого тела [1, 2]: создание, реконструкция и интерполяция. К первой группе относится набравшее популярность в последнее время 3D-сканирование, а также 3D-скульптинг — моделирование человеческого тела как трехмерной скульптуры в специальном для этих целей программном обеспечении. Ко второй группе — методы, позволяющие воссоздать модель по набору неструктурированных (или частично структурированных) данных [3]. Полученное представление должно соответствовать исходным данным с меньшим количеством ошибок и шума, а также позволять отслеживать характеристики и измерения, если это необходимо. Зачастую исходными при этом выступают модели из баз данных трехмерных сканов [4]. В третьей группе объединены методы, создающую модель путем деформации некоторой заданной базовой модели, в соответствии с установленными математическими ограничениями. Такой подход также называют параметрическим моделированием [5]. Процесс разделен на два этапа: построение поверхности сеточной структуры и ее аппроксимация неравномерными патчами. Сеточная структура необходима для устранения ошибок, связанных с недостатком или искажением информации при сканировании объекта. Аппроксимация поверхности осуществляется оригинальным методом построения «четырехугольного» каркаса с последующим представлением ячеек каркаса линейными поверхностями Кунса.
Исходными данными для построения модели является 3D-модель женского манекена стандартной формы, полученная трехмерным сканированием. Входная модель имеет полигональную структуру: множество точек tij(xij, yij, zij), соединенных в треугольные полигоны pi = (ti1, ti2,ti3), 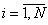 ,
, 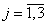 , где N — количество полигонов. На этапе построения сеточной структуры исходная модель разбивается на множество горизонтальных сечений hi, содержащих одинаковое количество точек {vij}, отсортированных по полярному углу и равноотстоящих друг от друга
, где N — количество полигонов. На этапе построения сеточной структуры исходная модель разбивается на множество горизонтальных сечений hi, содержащих одинаковое количество точек {vij}, отсортированных по полярному углу и равноотстоящих друг от друга 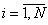 ,
, 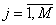 , где N — количество сечений, M — количество точек в сечениях. Одним из основных свойств формы манекена является симметричность относительно плоскости xOz, поэтому исходные сечения подвергаются симметризации — определению средних значений между левыми и правыми половинами относительно оси симметрии, а затем сглаживанию — интерполяции сплайнами третьего порядка.
, где N — количество сечений, M — количество точек в сечениях. Одним из основных свойств формы манекена является симметричность относительно плоскости xOz, поэтому исходные сечения подвергаются симметризации — определению средних значений между левыми и правыми половинами относительно оси симметрии, а затем сглаживанию — интерполяции сплайнами третьего порядка.
Модель, состоящая из сечений hi, используется для аппроксимации патчами Кунса. Первым шагом аппроксимации является определение характерных точек для каждого i-го сечения из hi. Для снижения вычислительной нагрузки расчеты выполняются по полусечениям, по окончанию расчета линии каркаса отображаются относительно оси симметрии манекена. Каждое i-ое полусечение рассматривается как кусочно-линейная функция y(x) и выражается в параметризованном виде функциями x(s) и y(s). Параметром s выступает накопленная (суммарная) длине, то есть при s0 = 0
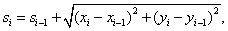
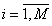 .
.
Для x(s) и y(s) определяются характерные точки, в которых первая производная равна нулю. Характерными признаются также точки начала и конца i-го полусечения.
Таким образом, перед этапом аппроксимации имеется N полусечений по M точек, при этом mi из них — характерные точки {pij}, 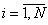 ,
, 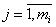 . Под построением каркаса подразумевается соединение точек сечений таким образом, чтобы они образовывали четырехугольную сетку, в узлах которой находились характерные точки. Построение каркаса осуществляется в три этапа: соединение точек переднего, заднего и бокового контуров; определение вертикальных ребер патчей; определение горизонтальных ребер патчей.
. Под построением каркаса подразумевается соединение точек сечений таким образом, чтобы они образовывали четырехугольную сетку, в узлах которой находились характерные точки. Построение каркаса осуществляется в три этапа: соединение точек переднего, заднего и бокового контуров; определение вертикальных ребер патчей; определение горизонтальных ребер патчей.
Соединение точек контуров происходит вертикальными линиями, при этом точки переднего и заднего контуров определяются как начало и конец полусечений; точки бокового контура определяются, как характерные точки, имеющие наибольшую координату по оси y и x-координату в интервале [–L1, L1], где L1 — эмпирически определяемое ограничение.
Определение вертикальных ребер патчей происходит путем попарного сравнения соседних полусечений по следующему алгоритму (пусть сравниваем i-ое и (i+1)-ое полусечения):
1. Определяются все евклидовы расстояния {αk}, 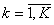 , между {pij} и {pi+1j}, при этом, если mi < mi+1, то K = mi+1, если mi+1 < mi, то K = mi, если mi = mi+1, то K = mi+1 = mi;
, между {pij} и {pi+1j}, при этом, если mi < mi+1, то K = mi+1, если mi+1 < mi, то K = mi, если mi = mi+1, то K = mi+1 = mi;
2. Определяются минимальные расстояния {βr}, 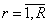 , из {αk}, при этом, если mi < mi+1, то для каждой точки из {pij} и R = mi, если mi+1 < mi, то для каждой точки из {pi+1j} и R = mi+1, если mi = mi+1, то R = mi+1 = mi;
, из {αk}, при этом, если mi < mi+1, то для каждой точки из {pij} и R = mi, если mi+1 < mi, то для каждой точки из {pi+1j} и R = mi+1, если mi = mi+1, то R = mi+1 = mi;
3. Расстояния {βr} проверяются на условие βr < L2, где L2 — эмпирически определяемое ограничение, если условие не выполняется — расстояние удаляется из {βr};
4. Соединяются соответствующие расстояниям {βr} характерные точки.
Определение горизонтальные ребер патчей выполняется путем соединения характерных точек по горизонтали по линиям соответствующих полусечений. При этом характерная точка соединяется с соседними характерными точками слева и справа, если выполняется одно из двух условий: у точки имеется одно вертикальное соединение, либо снизу, либо сверху; у точки вообще нет соединений. На характерных уровнях горизонтальные ребра проводятся вне зависимости от выполнения описанных выше условий.
Линии полученного каркаса аппроксимируются полиномами третьей степени, при этом линия каркаса представляет собой ломаную в пространстве, то есть множество точек p = {pi(xi, yi, zi)}, 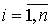 , где p0 и pn — характерные точки. Вектор-функция, описывающая аппроксимирующую кривую, имеет вид [6]:
, где p0 и pn — характерные точки. Вектор-функция, описывающая аппроксимирующую кривую, имеет вид [6]:
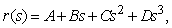
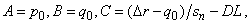
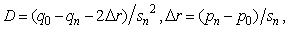
где q0, qn — касательные к кривой p в точках p0 и pn соответственно, параметр s — накопленная длина аппроксимируемой кривой.
Касательные q0 и qn определяются с учетом линий каркаса, примыкающих в точках p0 и pn. Расчет касательной q0 происходит в несколько этапов:
1. Определяются вектора k0 в точке p0 по формуле: 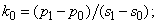
2. Рассчитываются вектора k1,…,km для всех m линий, примыкающих к точке p0 по формуле: 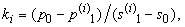
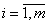 , где (i) –порядковый индекс линии, примыкающей к точке p0;
, где (i) –порядковый индекс линии, примыкающей к точке p0;
3. Для всех возможных пар векторов из {k0,…,km} определяются нормали N0,…,Nz, направленные от модели, 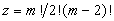 ;
;
4. Находится средняя нормаль 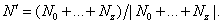
5. Рассчитывается проекция k0 на плоскость, нормалью которой является N' по формуле 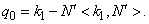
Аналогичным образом определяется вектор qn. Если линия, образующая границу патча, представляет собой отрезок, соединяющий две характерные точки, то касательные вектора будут определяться по следующим формулам: 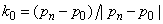 ,
, 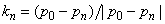 .
.
По четырем кривым, образующим патч p(i)(s(i)) и соединяющим их точкам pi, 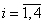 , строится линейная поверхность Кунса, которая описывается векторной функцией [7]:
, строится линейная поверхность Кунса, которая описывается векторной функцией [7]:
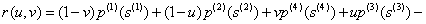
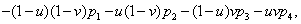
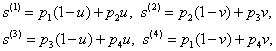
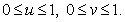
Исследование результатов построения базовой модели проводиться на трех различных манекенах. На рисунке 1 приведены их аппроксимированные модели с каркасными линиями, при количестве сечений разбиения N = 50.
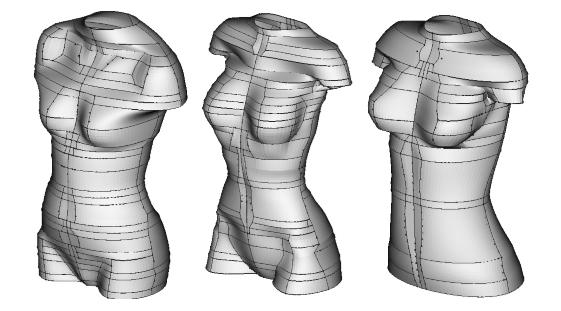
Рис. 1. Аппроксимированные патчами модели с каркасными линиями (1, 2, 3 слева направо)
В таблице 1 представлены результаты зависимости количества патчей P и среднего количества характерных точек в сеченииKот изменения N.
Таблица 1
Зависимость патчей и характерных точек от сечений разбиения
|
Параметр |
Значения параметра |
|||||
|
N |
30 |
50 |
70 |
90 |
110 |
130 |
|
Модель 1 |
||||||
|
P |
118 |
164 |
192 |
226 |
226 |
236 |
|
K |
9,533333 |
10,64 |
11,05714 |
10,51111 |
10,58182 |
10,18462 |
|
Модель 2 |
||||||
|
P |
130 |
216 |
272 |
316 |
370 |
394 |
|
K |
14,8 |
15,24 |
15,62857 |
15,42222 |
15,6 |
15,81538 |
|
Модель 3 |
||||||
|
P |
88 |
136 |
194 |
220 |
242 |
278 |
|
K |
11,86667 |
12,64 |
12,51429 |
12,8 |
12,69091 |
13,13846 |
Зависимость количества патчей от количества сечений разбиения схожа с экспоненциальным законом. Это дает возможность предполагать, что с увеличением количества сечений количество патчей приблизиться к некоторой постоянной величине. Среднее количество характерных точек при изменении количества сечений остается, с некоторым колебанием, постоянным, хотя общее количество характерных точек растет.
Для оценки эффективность аппрокисмации используются три показателя, рассчитываемых для одинокого количества горизонтальных сечений исходной модели и аппроксимированной. Сравнение показателей происходит путем расчет среднеквадратичного отклонения, а именно для каждого из трех показателей по формуле:
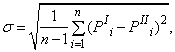
где PIi — i-ое значение показателя для исходной модели, PIIi — i-ое значение показателя для аппроксимированной модели, n — количество сечений. В качестве показательней используются следующие метрики.
Периметр i-го сечения: 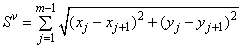 , где m — количество точек сечения, vj(xj, yj) — j-ая точка сечения.
, где m — количество точек сечения, vj(xj, yj) — j-ая точка сечения.
Периметр обхвата i-го сечения: 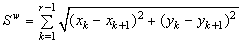 , где r — количество точек обхвата, wk(xk, yk) — k-ая точка обхвата.
, где r — количество точек обхвата, wk(xk, yk) — k-ая точка обхвата.
Дескриптор формы i-го сечения: 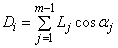 , где Lj — расстояние, в плоскости сечения, от центра масс сечения, до j-ой точки сечения,
, где Lj — расстояние, в плоскости сечения, от центра масс сечения, до j-ой точки сечения, 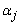 — разница по модулю между полярным углом j-ой точки сечения и углом
— разница по модулю между полярным углом j-ой точки сечения и углом 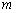 , m — количество точек в сечении.
, m — количество точек в сечении.
Результаты расчета показателей для каждой из моделей в зависимости от количества сечений представлены в таблице 2.
Таблица 2
Значения оценочных показателей для каждой из моделей
|
Параметры |
Значения параметра |
||||
|
N |
30 |
50 |
70 |
90 |
110 |
|
Модель 1 |
|||||
|
Sv |
1,195190023 |
0,870561914 |
0,831728362 |
0,883038342 |
0,897629057 |
|
Sw |
1,219116891 |
0,896300327 |
0,855218938 |
0,903345379 |
0,91269661 |
|
D |
37,86288926 |
28,36280151 |
26,82945364 |
28,12036441 |
27,97105915 |
|
Модель 2 |
|||||
|
Sv |
0,933634918 |
0,755565515 |
0,735464695 |
0,726110969 |
0,654140284 |
|
Sw |
0,953651178 |
0,771745333 |
0,749982053 |
0,736742674 |
0,661739855 |
|
D |
29,78629232 |
23,88449441 |
23,19878735 |
22,59209332 |
20,16706729 |
|
Модель 3 |
|||||
|
Sv |
1,047402781 |
0,974518142 |
0,939819871 |
0,962832618 |
0,923070174 |
|
Sw |
1,082958534 |
1,010027799 |
0,972639357 |
0,991421459 |
0,94608797 |
|
D |
33,86824188 |
31,66008576 |
30,34981363 |
30,6831071 |
28,95489496 |
На основании полученных результатов можно сделать вывод о том, что формы аппроксимированных моделей, при увеличении количества сечений до 70, становятся более схожими с исходными моделями, так как значения среднеквадратичного отклонения, рассчитанные по показателям, уменьшаются. Дальнейшее увеличение количества сечений приводит к ухудшению схожести. Это связано с тем, что слишком частое разбиение приводит большому количеству небольших патчей, которые, в свою очередь, при аппроксимации поверхностями Кунса, взывают излишние искривления поверхности.
Литература:
1. Lin S.-F., Chien S.-C. Create a Virtual Mannequin Through the 2-D Image based Anthropometric Measurements and Radius Distance Free Form Deformation, International Journal of Advanced Computer Science and Applications (IJACSA), 2011, Vol. 2, № 4, pp. 60–67.
2. Magnenat-Thalmann N., Seo H., Cordier F. Automatic modeling of animatable virtual humans — a survey, 3-D Digital Imaging and Modeling (3DIM), 2003, pp. 2–11.
3. Buxton B., Dekker L., Douros I., Vassilev T. Reconstruction and Interpretation of 3D Whole Body Surface Images, Scanning Proceedings, 2002.
4. http://store.sae.org/caesar/ (дата обращения: 30.03.2014)
5. Фроловский В. Д. Компьютерное проектирование манекенов и одежды. Трехмерные модели и математические методы. Издательский Дом: LAP LAMBERT Academic Publishing. Saarbrucken, Germany, 2012. 269 с.
6. Ильин М. Е. Аппроксимация и интерполяция. Методы и приложения. Учебное пособие. Рязань, 2003. 56 с.
7. Голованов Н. Н. Геометрическое моделирование. М.: Издательство Физико-математической литературы, 2002. 472 с.











