Статистика отказов шин легковых автомобилей
Авторы: Дамзен Виктор Александрович, Елистратов Сергей Валерьевич
Рубрика: 9. Транспорт
Опубликовано в
III международная научная конференция «Технические науки в России и за рубежом» (Москва, июль 2014)
Дата публикации: 17.06.2014
Статья просмотрена: 843 раза
Библиографическое описание:
Дамзен, В. А. Статистика отказов шин легковых автомобилей / В. А. Дамзен, С. В. Елистратов. — Текст : непосредственный // Технические науки в России и за рубежом : материалы III Междунар. науч. конф. (г. Москва, июль 2014 г.). — Т. 0. — Москва : Буки-Веди, 2014. — С. 115-118. — URL: https://moluch.ru/conf/tech/archive/90/5884/ (дата обращения: 24.04.2025).
Автомобиль представляет собой сложную систему состоящей из множества элементов. Каждый из элементов вносит свой вклад в надежность всей системы. Одним из таких элементов являются автомобильные шины. И хотя процесс замены неисправного элемента на исправный не представляет больших трудностей автомобиль выходит из строя. Следовательно, происходит снижение показателей надежности транспортного средства. При отдельном рассмотрении автомобильных шин к ним применимы все свойства надежности: безотказность, долговечность, ремонтопригодность, сохраняемость. В большинстве случаев надежность шин оценивают по совокупности показателей. Показателями, определяющими надежность шины, могут быть износ протектора (до минимально допустимой величины протектора), пробои и порезы, усталостные дефекты каркаса или все показатели сразу. Так в [1] представлены функции вероятности безотказной работы грузовых шин по перечисленным показателям. Примеры распределения партии восстановленных шин снятых с эксплуатации по пробегу и определение ожидаемого пробега шин представлены в [2].
На основании статистических данных по обращениям в шиномонтажную мастерскую проведен анализ надежности автомобильных шин. В качестве показателей надежности предлагается использовать вероятность безотказной работы шин, вероятность отказов, частота отказов, интенсивность отказов, гамма-процентный ресурс шин, закон распределения выхода шин из строя по пробегу. Такие свойства надежности как ремонтопригодность и сохраняемость автомобильных шин в данной работе не рассматривались. При сборе информации о ресурсе шин фиксировался факт снятия шин с эксплуатации и ремонтные операции в статистических данных не отражались. В соответствии с нормативной документацией завод-изготовитель автомобильных шин гарантирует ее сохраняемость в течении 5 лет с даты изготовления.
По исходным данным было проведено распределение шин по пробегу со следующими параметрами: количество интервалов разбиения m = 15; длина интервалов Δt = 11334 км. В результате получена гистограмма частот распределения отказов шин по пробегу (рис. 1).
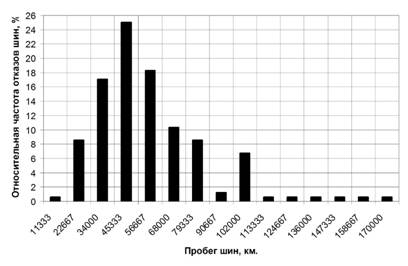
Рис. 1. Гистограмма частот распределения отказов шин по пробегу
В соответствии с [3] вероятностью безотказной работы называется количественная мера того, что при определенных условиях эксплуатации в заданном интервале времени или в пределах заданной наработки не произойдет ни одного отказа и определяется по формуле:
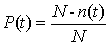 (1)
(1)
где: N — число испытываемых объектов; n(t) — число отказавших элементов за время t
Вероятностью отказа называется количественная мера того, что при определенных условиях эксплуатации в заданном интервале времени возникает хотя бы один отказ. Отказ и безотказная работа являются событиями несовместными и противоположными. Следовательно, вероятностью отказа определяется по формуле [3]:
Q(t) = 1 — P(t) (2)
Расчетные значения по формулам (1) и (2) представлены в виде графиков на рис. 2. По графику можно определить гамма-процентный ресурс шин. Он определяется как суммарная наработка, в течение которой объект не достигнет предельного состояния с вероятностью гамма, выраженной в процентах [4]. Тогда 90 % гамма-процентный ресурс составит 23000 км пробега, что соответствует вероятности безотказной работы шин равной 0,9. кроме того из анализа интегральных функций (рис. 2) видно, что 50 % вероятность безотказной работы шин составляет 45000 километров пробега. Частотой отказов по статистическим данным называется отношение числа отказавших элементов в единицу времени к первоначальному числу работающих (испытываемых) и определяется по формуле [3]:
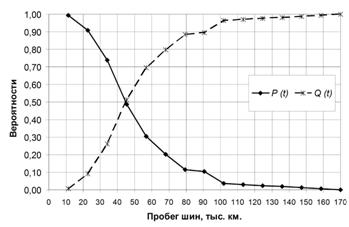
Рис. 2. Интегральные функции безотказной работы P(t) и отказов Q(t)
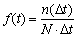 (3)
(3)
где: n(Δt) — число отказавших элементов в интервале времени от (t — Δt)/2 до (t + Δt)/2
Интенсивностью отказов по статистическим данным называется отношение числа отказавших изделий в единицу времени к среднему числу изделий, исправно работающих в данный отрезок времени [3].
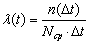 (4)
(4)
где: Nср — среднее число исправно работающих изделий в интервале Δt
Величины частоты и интенсивности отказов имеют одинаковый порядок значений и размерность, поэтому могут изображаться в одних координатах. Результаты расчетов по формулам (3) и (4) представлены на рис. 3.
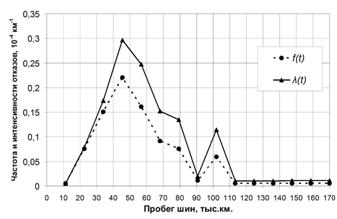
Рис. 3. График зависимости частоты f(t) и интенсивности l(t) отказов шин от пробега
Среднее время (пробег) безотказной работы вычисляется по формуле [3]:
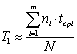 (5)
(5)
где: tсрi находится по следующей формуле: tсрi=(ti-1+ ti)/2
где: ti–1 — время начала i-го интервала; ti — время конца i-го интервала
В результате расчетов по формуле (5) получаем, что средний пробег безотказной работы шин составлякт T1 = 50790 км.
В общем случае результаты наблюдений выхода шин из строя (рис. 1) могут подчиняться некоторому теоретическому закону распределения. Проверку соответствия теоретического распределения проводится с помощью критерия соответствия c2. Выбранное теоретическое распределение подтверждается, если выполняется условие [5]:
c2 < c2a (6)
где: c2 — расчетное значение параметра; c2a — теоретическое значение параметра
Для 10 %-ного уровня значимости и числа степеней свободы равном 6, табличное значение c2a = 10,645 [5]. При подборке теоретических распределений получены следующие результаты:
1. Нормальное распределение — c2 = 39,16
2. Гамма распределение — c2 = 14,97
3. Логарифмически нормальное распределение — c2 = 9,26
Условие (6) выполняется только для логарифмически нормального распределения:
9,26<10,645
Следовательно, при определении надежности шин принимается логарифмически нормальный закон распределения. На рис. 4 представлены кривые теоретического распределения и экспериментальных данных.
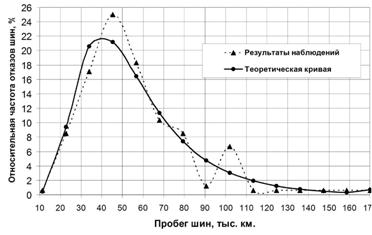
Рис. 4. Теоретическое распределение и экспериментальные данные отказов шин
Соответствие экспериментальных данных логарифмически нормальному закону распределения означает, что случайная величина (пробег шины) зависит от большого числа независимых факторов [6]. Действительно, на надежность автомобильных шин влияют многие факторы: качество шин, состояние дороги, скорость автомобиля, мастерство водителя, давление в шинах, углы установки колес и другие.
На основании представленных данных можно сделать следующие выводы. Статистические данные по пробегу шин легковых автомобилей соответствуют логарифмически нормальному закону распределения. В соответствии с гистограммой (рис. 1) наибольшее количество шин, примерно 42 %, выходят из строя при пробеге 45–56 тысяч километров. А по теоретическому закону максимум выходов из строя шин (41,5 %) приходится на пробег 34–45 тысяч километров (рис. 4). В тоже время средний пробег безотказной работы составляет 50790 километров. Наибольший пробег шин доходит 170000 километров. До пробега более 90000 километров «доживают» лишь 12 % шин и вероятность их отказа составляет 0,9. Однако это показывает, что имеется возможность увеличения надежности автомобильных шин в эксплуатации за счет повышения качества факторов, определяющих их ресурс.
Литература:
1. Третьяков О. Б. Автомобильные шины. Конструкция, механика, свойства, эксплуатация / О. Б. Третьяков, В. А. Гудков, А. А. Вольнов, В. Н. Тарновский. — М.: КолосС, Химия, 2007. — 432 с.
2. Евзович В. Е. Восстановление изношенных пневматических шин / В. Е. Евзович — М.: Автополис-плюс, 2005. — 624 с.
3. Корчагин А. Б. Надежность технических систем и техногенный риск: учебное пособие в двух частях. Часть 2. Практикум / А. Б. Корчагин, В. С. Сердюк, А. И. Бокарев. — Омск: Издательство ОмГТУ, 2011. — 140 с.
4. Курчаткин, В.В Надежность и ремонт машин / В. В. Курчаткин, Н. Ф. Тельнов, К. А. Ачкасов и др.; под ред. В. В. Курчаткина. — М.: Колос, 2000. — 776 с.
5. Львовский Е. Н. Статистические методы построения эмпирических формул / Е. Н. Львовский. Учебное пособие для втузов. — 2-е изд., перераб. и доп. — М.: Высшая школа, 1988. — 239 с.
6. Айвазян С. А. Прикладная статистика: Основы моделирования и первичная обработка данных. Справочное издание / С. А. Айвазян, И. С. Енюков, Л. Д. Мешалкин. — М.: Финансы и статистика, 1983. — 471 с.











