Разработка и совершенствование методов получения и обработки информации для задач управления крупным предприятием
Автор: Самарин Илья Вадимович
Рубрика: 3. Автоматика и вычислительная техника
Опубликовано в
III международная научная конференция «Технические науки в России и за рубежом» (Москва, июль 2014)
Дата публикации: 25.06.2014
Статья просмотрена: 629 раз
Библиографическое описание:
Самарин, И. В. Разработка и совершенствование методов получения и обработки информации для задач управления крупным предприятием / И. В. Самарин. — Текст : непосредственный // Технические науки в России и за рубежом : материалы III Междунар. науч. конф. (г. Москва, июль 2014 г.). — Т. 0. — Москва : Буки-Веди, 2014. — С. 48-54. — URL: https://moluch.ru/conf/tech/archive/90/5922/ (дата обращения: 24.04.2025).
Представлена методика применения метода анализа иерархий для определения параметров целевой функции оптимизационной задачи, из решения которой устанавливаются структура и характеристики среднесрочного плана деятельности крупного предприятия. Указанный экспертно-расчётный метод — комбинированный, включающий метод решающих матриц и метод парных сравнений.
За счёт сопряжения методов решающих матриц и парных сравнений удается получить логически законченную процедуру обработки информации для задач управления крупным предприятием.
Ключевые слова: агрегатный показатель, анализ, блок-схема, динамический режим, иерархия, матрица, метод, парные сравнения, план, решающая матрица, стратегическое планирование, структуризация, формализация, целевая функция.
В работах [1–3], посвящённых совершенствованию методов прогнозирования и стратегического планирования на крупном предприятии высокотехнологической отрасли, рассматривался динамический режим стратегического планирования. Было показано, что целевая функция, в обобщённом виде определяющая качество деятельности предприятия в очередном плановом периоде, может считаться линейной функцией показателей эффективности отдельных предполагаемых мероприятий. Коэффициенты этой линейной функции определяют значимости различных мероприятий, т. е. их вклады в продвижении к обобщённой стратегической цели в течение очередного планового периода. Было показано, что методически наиболее сложной частью научной проблемы, связанной с реализацией предложенного подхода, является разработка методики обработки информации для определения этих коэффициентов.
Процедура определения параметров целевой линейной функции для стратегического планирования,может бытьоснована на анализе экспертно-расчётными методами иерархии целевых установок деятельности предприятия. Ниже рассматривается существо метода анализа иерархий [2–4]. Этот метод — комбинированный, включающий в себя метод парных сравнений [4] и метод решающих матриц [5].
Метод решающих матриц [5] предназначен для определения величин относительных вкладов факторов нижнего уровня в достижение общей стратегической цели или степени продвижения к ней. Для предприятия факторами нижнего уровня могут быть отдельные работы (мероприятия).
Как следует из самого названия метода, он работает с иерархическими схемами. Пример возможной иерархии целевых установок предприятия представлен на рис. 1.
Иерархическая схема — графическое изображение соподчиненности целевых установок и их связи с основной (стратегической) целью. Иерархические уровни — это уровни, на которых расположены однородные в системном плане факторы. На рисунке 1 для примера представлена 6-ти уровневая иерархия. 6-й уровень — это уровень отдельных мероприятий, вклады которых в достижение стратегической цели требуется определить.
Понятно, что чем больше и сложнее экономическая система, тем более сложна многоуровневая иерархическая схема её деятельности. И, как правило, иерархии реальных экономических систем по всем уровням, кроме 1-го, несовершенны. В этих условиях довольно затруднительно выявить влияние факторов нижнего уровня на агрегатную цель — слишком все переплетено и запутано в иерархической схеме. Для выявления такой связи применяется метод решающих матриц.
Перед началом рассмотрения существа этого метода логично упреждающе ответить на естественный вопрос: зачем нужно рассматривать иерархию, не проще ли попытаться непосредственно определить вклад каждого мероприятия в агрегатный показатель?
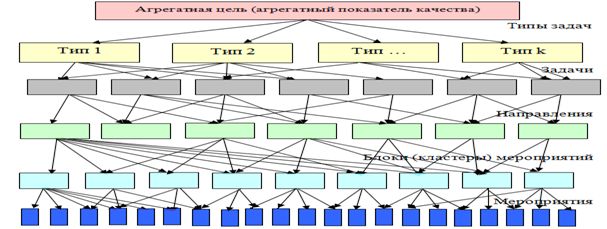
Рис.1. Иерархическая схема взаимосвязи выполняемых предприятием мероприятий (работ) с его обобщённой стратегической целью
Ответ заключается в следующем: для этого придется провести большую аналитическую работу, разработать большое количество математических моделей. Это очень сложно при динамическом режиме планирования, который производится почти непрерывно при хроническом дефиците времени. Поэтому наряду с расчётными схемами приходится также использовать экспертные оценки.
Отсюда следует, что для определения вкладов различных мероприятий в агрегатный показатель качества деятельности предприятия необходимо привлечение квалифицированных экспертов. Но на современных больших предприятиях нет таких специалистов, которые знают и понимают все проблемы на всю их широту и глубину. Руководители отслеживают стратегические направления, следят за внешней системной средой, за конкурентами, за рынками. А инженеры и технологи, наоборот, почти все знают о конструкциях технических систем, понимают многие технологические тонкости, но имеют недостаточное представление о стратегии фирмы, об особенностях её финансовой устойчивости, о способах позиционирования на рынках.
В итоге, получается, что в больших экономических системах как правило никто никогда не видит проблем целиком. Поэтому естественно возникает идея разделить процесс выработки рационального решения при помощи квалифицированных экспертов таким образом, чтобы использовать знания каждого специалиста на уровне его максимальной компетенции.
Это достигается за счёт использования иерархии, которая как раз предназначена для интеграции знаний разных специалистов, каждый из которых видит только свою часть общей проблемы.
Только за счёт применения иерархического схемы формирования решения значительно повышается его точность. Но это — только первый шаг в этом направлении. Условно его можно назвать вертикальным.
Вторым важным шагом — горизонтальным — является применение метода парных сравнений для ранжирования значимостей промежуточных целей, а также мероприятий (работ) — вдоль иерархического уровня. Это — наиболее трудоёмкий, но и наиболее точный экспертный метод, который в ряде случаев позволяет получать точность результата на уровне методов математического моделирования.
Существо метода парных сравнений изложено в работе [4]. Метод основан на выводах психофизических исследований: оказывается люди — эксперты — очень часто (точнее — практически всегда) ориентируются в ситуации значительно лучше, чем они сами себе это представляют. Надо только предоставить им наиболее комфортные условия для проведения экспертизы, дать возможность сосредоточиться на рассматриваемом конкретном вопросе.
В последней фразе слово «сосредоточиться» — ключевое. Метод парных сравнений доводит эту процедуру до логического предела — эксперту предлагается сравнивать друг с другом важности факторов попарно, т. е. на каждой фазе анализа учитывать минимально возможное количество объектов сравнения.
Результаты сравнений сводятся в квадратную матрицу парных сравнений, которую далее обозначим D. Экспертно сформированная матрица D парных сравнений значимости различных факторов имеет вид:
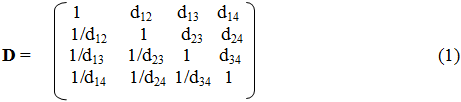
Элементами dij матрицы являются величины экспертно определяемых отношений значимостей j-го фактора по отношению к значимости i-го фактора. Значимость понимается в смысле некоторой цели. Заметим, что в работе Саати используются обратные числа, когда значимости факторов сравниваются по столбцам. Но, как показала практика, экспертам удобнее заполнять матрицу не по столбцам, а по строкам.
Естественно, что матрица D должна быть обратносимметричной, т. к. значимости каждого из двух факторов при сравнении в масштабах противоположного фактора должны находиться в обратной зависимости: dij = 1/dji. Отсюда следует простое и очевидное правило: dii = 1 для всех i, т. е. все диагональные элементы всех матриц парных сравнений равны 1.
В идеальном случае при совершенных суждениях dik = dij´djk для всех i,j,k; при этом D называется согласованной матрицей. Подобные матрицы образуются, когда сравнения основаны на точных измерениях. В общем случае может оказаться, что dik≠dij´djk, т. е. относительные суждения могут быть не согласованы друг с другом (не транзитивны). Необходимо отметить, что это не исключительный, а наоборот — типичный случай, который встречается при решении практических задач.
Следует заметить, что если до проведения экспертных оценок имеется предварительная информация об относительной значимости некоторых пар факторов (например, информация, полученная в результате расчётов по точным частным математическим моделям), то она легко встраивается в матрицу парных сравнений, а результаты обработки матрицы становятся ещё более точными. Таким образом, метод парных сравнений не противопоставляет различные виды информации, а использует их по принципу дополнительности. Это — очень важно для понимания существа этого экспертно-расчётного метода.
Для того, чтобы от относительных значимостей факторов перейти к абсолютным, необходимо обработать матрицу парных сравнений.
Существуют несколько способов (алгоритмов) такой обработки. Например, в работе [4], подробно описан метод, основанный на определении собственных значения и вектора x линейного матричного оператора, который представляется обратносимметричной матрицей D:
D´x = ´x, (2)
где

k — общее количество сравниваемых факторов, равное числу строк или столбцов в квадратной матрице D, т. е. её размерности.
Нормировка суммы компонент вектора значимостей x на 1 — дань наглядности: удобнее всего пользоваться некоторой стандартной шкалой значимостей, а изменения масштаба измерения значимостей мероприятий не повлияет на рациональное стратегическое плановое решение.
Реализация метода собственного значения предполагает применение некоторого алгоритма для определения и нормализованного условием (3) вектора x значимостей. Невозможность получения аналитического решения — основной недостаток метода собственного значения, поскольку использование алгоритма численного решения (2–3) делает результат менее наглядным.
Можно предложить другой достаточно простой и, что очень важно, не менее точный, метод определения компонентов вектора x, который, с одной стороны, допускает получение аналитического решения, а с другой — дает результаты, достаточно близкие по отношению к методу собственного значения (в большинстве случаев величина относительного рассогласования — несколько процентов).
В основу этого метода положено известное правило наименьшей суммы квадратов. Однако оно должно быть применено не к величинам dij, а к логарифмам этих величин, т. к. производится обработка результатов определения относительных значений. Поэтому логично минимизировать сумму квадратов разности логарифмов
Ln(dij) — Ln(xj/xi)
Таким образом, приходим к следующей оптимизационной задаче.
Определить
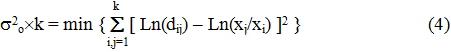
при ограничении — равенстве (3).
Результат в (4) записан несколько необычно в виде 2о´k. Это сделано специально для того, чтобы использовать о для характеристики качества полученного решения при различных значениях k, поскольку корректно можно сопоставлять друг с другом не значения 2о´k, а средние значения .
Можно показать, что эта оптимизационная задача имеет решение:
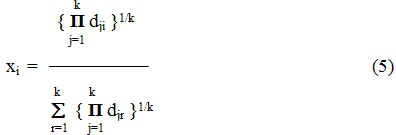
Таким образом, получается простой и наглядный результат: относительные значимости xi пропорциональны средним геометрическим величинам элементов матрицы A парных сравнений, расположенных на каждой строке. Очень важно, что для результата можно получить аналитическое выражение.
В результате обработки матриц парных сравнений оказывается возможным получить достаточно точные оценки относительных значимостей xi различных факторов. Очень часто эти оценки оказываются не только приемлемо точными, а удивительно точными.
Основная причина этого заключается в следующем. Легко показать, что количество определяемых экспертами элементов матрицы парных сравнений превышает количество независимых компонентов xi в k/2 раз, т. е. имеется дополнительная информация, полезная для уточнения xi. Как известно, дополнительная информация обычно снижает общую неопределённость. Для наглядности можно сказать, что относительные значимости факторов измеряются не одним, а как бы совокупностью различных измерителей с разными масштабами (в разной системе измерений). И хотя часто эти измерители — грубые, наложение результатов измерений повышает общую точность оценок величин xi.
Следующий этап — сопряжение результатов экспертиз, проведенных на разных иерархических уровнях для выхода на конечный результат — определение значимостей различных мероприятий (работ) для достижения стратегической цели. Эта операция производится методом решающих матриц [5]. Его существо заключается в следующем.
Предположим, что методом парных сравнений определены значимости отдельных направлений для успешности функционирования экономической системы. Если сумму этих значимостей нормировать на 1, то они могут быть представлены строкой или матрицей-строкой
x = (x1, x2, …… xk),
где k — общее количество рассматриваемых направлений деятельности.
Для перехода со 2-го на 3-й уровень необходимо отдельно рассматривать различные типы задач предприятия.
Для 1-го типа задач имеем следующий набор значимостей среднесрочных функциональных задач:
y1 = (y1, y2, y3, ……….yr),
где r — максимальное количество функциональных задач в рассматриваемом плановом периоде. Заметим, что если какая-то среднесрочная задача не связана с 1-м типом деятельности предприятия, то соответствующий элемент матрицы-строки должен быть равен нулю.
Набор значений y1 формируется так же, как набор x: сначала по результатам экспертных оценок составляется обратносимметричная матрица парных сравнений относительных значимостей факторов 3-го уровня для достижения 1-й промежуточной цели. Вектор y1 образуется в результате её обработки. В нём отличными от нуля компонентами будут только те, которые способствуют достижению 1-й промежуточной цели; остальные компоненты y1, не влияющие на реализацию 1-й промежуточной цели, должны быть равны нулю.
Процедура формирования остальных строк, соответствующих y2, y3….yk — аналогична. Точно такая же процедура (составление матриц парных сравнений для значимых факторов и её последующая обработка) применяется и для других иерархических уровней. Поэтому далее внимание на этом вопросе не акцентируется.
Для 2-го типа задач аналогично получаем набор значимостей функциональных задач:
y2 = (y21, y22, y23, ……….y2r),
То же самое делаем для других типов деятельности. Если теперь расположить эти строки одну под другой в виде прямоугольной таблицы, т. е. в виде матрицы, то получим следующее:
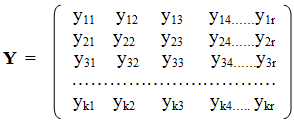
Далее в соответствие с [5] подобного вида матрицы будет называться решающими матрицами. Следует обратить внимание, что такие матрицы принципиально отличаются от матрицпарных сравнений по структуре, размерности и информационному содержанию: они более информационно насыщены, поскольку в ней содержится та же информация, что в нескольких (в данном случае — в r) матрицах парных сравнений. И, как правило, решающие матрицы — не квадратные.
И если теперь по правилам матричной алгебры слева умножить матрицу строку x на прямоугольную решающую матрицу Y, то в получившейся матрице-строке y* будут содержаться относительные значимости среднесрочных задач не по отношению к какому-то конкретному типу долгосрочных задач, а по отношению к агрегатной стратегической цели:
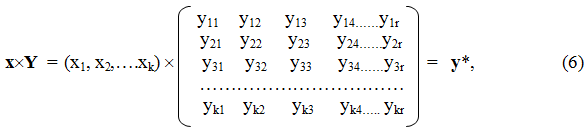
Действительно, рассмотрим 1-ю среднесрочную задачу. По отношению к 1-му типу деятельности её значимость равна y11, но значимость 1-го типа по отношению к агрегатной цели равна x1. Поэтому вклад 1-й среднесрочной задачи в общую цель по линии 1-го типа деятельности предприятия составит x1´y11. Аналогично, вклад 1-й среднесрочной задачи в общую цель по линии 2-го типа будет равен x2´y21, а суммарно от всех среднесрочных задач
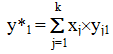
Но эта сумма как раз соответствует правилу умножения матриц (6). Поэтому матричное произведение действительно определяет относительные вклады различных среднесрочных задач в достижение общей цели.
В дальнейшем значимости y*s условно называются «абсолютными», т. к. они связаны не с промежуточной, а с агрегатной целью.
Таким образом, удалось определить значимости среднесрочных задач для достижения общей цели предприятия. Далее по аналогии: для установления относительных значимостей различных направлений деятельности предприятия определяем их значимости для решения каждой среднесрочной задачи и из полученных строк формируем прямоугольную решающую матрицу
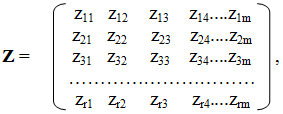
где m — общее количество основных направлений деятельности.
Если теперь матрицу-строку y* слева умножить на решающую матрицу Z, то получим абсолютные значимости направлений деятельности, которые содержатся в матрице-строке z*. Запишем это в компактной форме без обозначения всех матриц в виде таблиц:
y*´Z = X´Y´Z = z*
И здесь сумма всех элементов матрицы-строки z* равна 1.
Для установления относительных значимостей различных кластеров (блоков) мероприятий (работ) определяем их значимости для каждого направления деятельности и из полученных строк формируем прямоугольную решающую матрицу
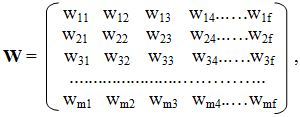
где f — общее количество кластеров мероприятий (работ) в рассматриваемом плановом периоде.
Умножая слева z* на W, получим вектор-строку абсолютных w* значимостей различных кластеров (блоков) мероприятий. Опять запишем это в компактной форме:
z*´W = x´Y´Z´W = w*
Последний шаг: для установления относительных значимостей различных мероприятий определяем их значимости в каждом кластере и из полученных матриц-строк формируем прямоугольную решающую матрицу U:
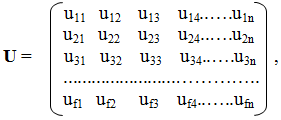
где n– количество мероприятий (работ).
Умножая слева w* наU, получим вектор-строку абсолютных u* значимостей различных мероприятий:
w*´U = x´Y´Z´W´U = u*
Для задачи анализа 6-ти уровневой иерархии получение матрицы u* является конечным результатом. В итоге определены значимости различных конкретных мероприятий (работ) для достижения основной цели предприятия.
Таким образом, при помощи метода решающих матриц удалось распутать сеть из промежуточных целей и связей между ними и получить достаточно понятный результат. Заметим, что часто применяемое условие нормировки суммы значимостей факторов на 1, которое сначала представлялось нечто искусственным, оказалось весьма полезным: не нужно заботиться о масштабах величин, пробираясь сквозь запутанную иерархическую схему — они согласуются автоматически.
Часто возникает вопрос о правилах построения иерархий. Формального и однозначного ответа на него нет. Более того, оказывается, что иерархию можно построить несколькими способами, и, как это не покажется странным на первый взгляд, все они могут оказаться правильными.
Дело в том, что иерархия — это не результат, а способ решения задачи. А, как известно, многие задачи могут быть решены множеством способов, и все решения будут верными. Другими словами, иерархия — это промежуточное и во многом субъективное звено, а объективен только конечный результат — значимости различных мероприятий (работ) для достижения стратегической цели.
Можно предложить несколько рекомендаций по построению иерархий.
Желательно, чтобы иерархические схемы отражали организационно-штатную структуру предприятий. Но, с другой стороны, часто предприятие вынуждено работать, существенно отклоняясь от этой структуры: появляются новые задачи, новые условия, приходят новые люди. Поэтому принцип соответствия реальности ранее принятой организационно-штатной структуре предприятия часто нарушается.
Иерархию следует подстраивать не под идеальных экспертов, а под располагаемый контингент специалистов. Их, конечно, можно дополнительно информировать и постепенно обучать, но существенно изменить их будет трудно. В этом следует отдавать себе полный отчёт. Поэтому иерархия должна учитывать структуру экспертного потенциала предприятия, адаптироваться к ней.
Очень желательно, чтобы на каждом иерархическом уровне факторы были сопоставимы — тогда экспертные оценки их относительных значимостей будут более точны. Для достижения этого часто можно применить искусственный прием: если один из факторов доминирует над другими, его можно представить в виде совокупности нескольких факторов меньшей значимости.
При построении иерархической схемы желательно отразить региональный или структурный аспект деятельности предприятия. Если у предприятия есть несколько филиалов или дочерних организаций, то целесообразно под них предусмотреть отдельный иерархический уровень. Тем более, что такие структуры — относительно стабильные факторы, если не долгосрочного, то среднесрочного уровня.
Следует отметить, что при формировании иерархических схем не обязательно придерживаться жёсткого требования соответствия некоторому количеству иерархических уровней. По отдельным факторам или группам факторов иерархическая схема может иметь разную размерность. Для этого достаточно задублировать наименования этого фактора на соседних уровнях.
Наконец, полезно учитывать ещё одно несложное правило. Желательно так построить иерархическую схему, чтобы на каждом уровне количество факторов, связанных с некоторой промежуточной целью, не превышало 15. Дело в том, что люди (эксперты) способны одновременно хорошо воспринимать совокупность 7±2 операндов (объектов, элементов, кластеров, понятий). При большем количестве они начинают путаться в суждениях. Поэтому 15 — это некоторый психологический предел, выше которого эффективность экспертных оценок может начать снижаться.
Следуя этим правилам, можно сформировать несколько экспериментальных иерархических схем, исследую которые впоследствии подобрать из них наиболее адекватные условиям функционирования предприятия и существующему в нем экспертному потенциалу.
Литература:
1. Самарин И. В. Формализация задачи обоснования среднесрочного плана деятельности для построения автоматизированной системы управления стратегического планирования на предприятии // ж. «Инновации и инвестиции» № 4 — М., 2014
2. Рябошапко В. А., Фомин А. Н. Основные положения методологии разработки антикризисных целевых программ (часть 1). Вестник Академии военных наук № 4(13) — М.:, 4-й филиал Воениздата, 2005.
3. Баскаков В. В., Федосеев С. А., Фомин А. Н. Научно-методические основы подготовки научно-педагогических кадров // МО РФ, Академия военных наук — М., ВА РВСН им. Петра Великого, 2011
4. Саати Т. Принятие решений. Метод анализа иерархий. Перев. с англ. Вачнадзе Р. Г. — М.: Радио и связь, 1993
5. Моисеев Н. Н. Математические задачи системного анализа. — М.: Наука, гл. ред. физ-мат. литературы, 1981
6. В. И. Смирнов. Курс высшей математики, Т.3, Ч.1 — М.: Наука, гл. ред. физ-мат. литературы, 1974
Ключевые слова
анализ, метод, стратегическое планирование, матрица, структуризация, план, иерархия, формализация, план, агрегатный показатель, блок-схема, динамический режим, парные сравнения, решающая матрица, целевая функция., целевая функцияПохожие статьи
Управление качеством строительных технологий на основе обобщенного критерия качества
В работе предложен новый подход к описанию и оптимизации интегрального критерия качества выбранных свойств системы методами нелинейного программирования, где в качестве параметризации выбираются стоимостные характеристики. Приведены примеры постаново...
Динамическое программирование в решении задачи оптимального размещения электронных компонентов системы управления
В статье изложен способ повышения эффективности проектирования электромонтажных схем системы управления технологическим оборудованием с использованием метода Р. Беллмана. Разработана математическая модель, позволяющая наилучшим образом разместить эле...
Программный комплекс оптимального выбора проекта распределенной вычислительной сети
В статье изложен способ повышения эффективности проектирования распределенной вычислительной сети. Разработаны математическая модель и программный комплекс оптимального выбора распределенной вычислительной сети. Результаты математического моделирован...
Кластеризация диагностических моделей и их выделение из конфигурационных наборов аппаратных архитектур реконфигурируемой системы функционального контроля и диагностики космического аппарата
В работе рассматриваются особенности математической формализации процессов формирования диагностических моделей контролируемых и диагностируемых бортовых систем космического аппарата в реконфигурируемом вычислительном поле. Предложена математическая ...
Математическая модель оптимизации структуры электромонтажной панели системы управления
В статье изложен метод повышения эффективности проектирования электромонтажных схем системы управления технологическим оборудованием с использованием математического моделирования. Разработана математическая модель оптимизации структуры электромонтаж...
Программный комплекс моделирования транспортных и пешеходных потоков на регулируемом перекрестке
В статье изложен способ повышения эффективности управления транспортными и пешеходными потоками на регулируемом перекрестке. Реализованы валидация, проектирование и верификация. Разработан программный комплекс моделирования регулируемого перекрестка...
Сравнение моделей качества программного обеспечения
В данной статье приводится пример разработки плана развития использования облачных технологий на предприятии на основе разработанной модели с использованием методов оптимизации — многокритериального линейного программирования, а также метода ограниче...
Методы оценки финансового состояния организации
В данной статье рассматривается понятие финансового состояния организации, а также его методы и подходы. Представлена авторская методика анализа, основанная на концепции Турманидзе Т. У., и составлена таблица порядка его проведения.
Определение обобщенной частотной характеристики эргатической системы по данным нормальной эксплуатации
Производится определение обобщенных характеристик целостной эргатической системы, как некоторой разомкнутой системы (определение передаточных функций человека-оператора и объекта в отдельности практически невозможно в связи с действием организмическо...
Разработка web-ориентированного программного модуля мониторинга формирования уровня компетентности студентов технических вузов на основе контрольных карт и гистограмм
В работе приведен анализ проблем компетентностного подхода в образовании, поставлена цель и задачи разрабатываемого программного модуля. Описана схема база данных и архитектура разработанного программного продукта, рассмотрены основные возможности, о...
Похожие статьи
Управление качеством строительных технологий на основе обобщенного критерия качества
В работе предложен новый подход к описанию и оптимизации интегрального критерия качества выбранных свойств системы методами нелинейного программирования, где в качестве параметризации выбираются стоимостные характеристики. Приведены примеры постаново...
Динамическое программирование в решении задачи оптимального размещения электронных компонентов системы управления
В статье изложен способ повышения эффективности проектирования электромонтажных схем системы управления технологическим оборудованием с использованием метода Р. Беллмана. Разработана математическая модель, позволяющая наилучшим образом разместить эле...
Программный комплекс оптимального выбора проекта распределенной вычислительной сети
В статье изложен способ повышения эффективности проектирования распределенной вычислительной сети. Разработаны математическая модель и программный комплекс оптимального выбора распределенной вычислительной сети. Результаты математического моделирован...
Кластеризация диагностических моделей и их выделение из конфигурационных наборов аппаратных архитектур реконфигурируемой системы функционального контроля и диагностики космического аппарата
В работе рассматриваются особенности математической формализации процессов формирования диагностических моделей контролируемых и диагностируемых бортовых систем космического аппарата в реконфигурируемом вычислительном поле. Предложена математическая ...
Математическая модель оптимизации структуры электромонтажной панели системы управления
В статье изложен метод повышения эффективности проектирования электромонтажных схем системы управления технологическим оборудованием с использованием математического моделирования. Разработана математическая модель оптимизации структуры электромонтаж...
Программный комплекс моделирования транспортных и пешеходных потоков на регулируемом перекрестке
В статье изложен способ повышения эффективности управления транспортными и пешеходными потоками на регулируемом перекрестке. Реализованы валидация, проектирование и верификация. Разработан программный комплекс моделирования регулируемого перекрестка...
Сравнение моделей качества программного обеспечения
В данной статье приводится пример разработки плана развития использования облачных технологий на предприятии на основе разработанной модели с использованием методов оптимизации — многокритериального линейного программирования, а также метода ограниче...
Методы оценки финансового состояния организации
В данной статье рассматривается понятие финансового состояния организации, а также его методы и подходы. Представлена авторская методика анализа, основанная на концепции Турманидзе Т. У., и составлена таблица порядка его проведения.
Определение обобщенной частотной характеристики эргатической системы по данным нормальной эксплуатации
Производится определение обобщенных характеристик целостной эргатической системы, как некоторой разомкнутой системы (определение передаточных функций человека-оператора и объекта в отдельности практически невозможно в связи с действием организмическо...
Разработка web-ориентированного программного модуля мониторинга формирования уровня компетентности студентов технических вузов на основе контрольных карт и гистограмм
В работе приведен анализ проблем компетентностного подхода в образовании, поставлена цель и задачи разрабатываемого программного модуля. Описана схема база данных и архитектура разработанного программного продукта, рассмотрены основные возможности, о...











