Конспект урока в 6-м классе по теме «Симметрия»
Автор: Козуб Светлана Владимировна
Рубрика: Методическая копилка: конспекты и карты уроков
Опубликовано в Школьная педагогика №1 (20) январь 2021 г.
Дата публикации: 08.11.2020
Статья просмотрена: 2799 раз
Библиографическое описание:
Козуб, С. В. Конспект урока в 6-м классе по теме «Симметрия» / С. В. Козуб. — Текст : непосредственный // Школьная педагогика. — 2021. — № 1 (20). — С. 33-36. — URL: https://moluch.ru/th/2/archive/184/5689/ (дата обращения: 24.04.2025).
Цели урока
Образовательные: повторение понятий осевой и центральной симметрий; подготовка учащихся к изучению геометрии, углубление имеющихся знаний; показать использование симметрии в жизни.
Развивающие: развитие творческой активности, познавательного интереса.
Воспитательные: воспитание умения работать в группах, внимательно слушать речь других.
В результате работы на уроке обучающиеся смогут: расширить знания по теме “Симметрия”, получить наглядное представление о проявлениях симметрии в различных областях науки и человеческой деятельности, развить навыки организации познавательной деятельности, получения информации; навыки сотрудничества и коммуникации.
Оборудование: компьютер, проектор, раздаточный материал (в том числе набор геометрических фигур: квадрат, равнобедренный треугольник, круг, правильный шестиугольник, трапеция и набор картинок: бабочка, здание, имеющее ось симметрии, цветок, имеющий центр симметрии и т. п.)
План урока
- Организационный момент.
- Самоопределение к учебной деятельности.
- Актуализация знаний. Определение темы и цели урока.
- Повторение и обобщение понятий «осевая симметрия», «центральная симметрия».
- Самостоятельная работа.
- Домашнее задание.
- Подведение итогов урока.
Ход урока
1.Организационный момент
Проверка готовности учащихся к уроку.
2. Самоопределение к учебной деятельности
— Какую тему мы изучали на предыдущих уроках?
Учащиеся отвечают: «Осевая симметрия», «Центральная симметрия».
—Сегодня мы продолжим изучение этой темы. Запишем тему урока «Симметрия».
— Какие преобразования фигур вы изучили? (Симметрия относительно прямой и симметрия относительно точки).
3.Актуализация знаний
Цитата: «Природа говорит языком математики». Галилео Галилей
—Как вы понимаете эти слова? (Ответы учащихся: «Чтобы понимать природу, уметь объяснять природные явления, надо многое знать, уметь использовать знания, полученные в частности на уроках математики»)
4. Повторение понятий осевой и центральной симметрий
1) Устная работа.
— Что означает слово «симметрия»? (Соразмерность, закономерность в расположении частей)
—Какие точки называются симметричными относительно прямой? (Точки M и N называются симметричными относительно прямой l, если отрезок MN перпендикулярен прямой l и в точке пересечения с этой прямой делится пополам).
— У вас на парте лежат фигуры. Поднимите те из них, которые имеют ось симметрии. (Все фигуры).
—Приведите примеры осевой симметрии в окружающем мире. (Учащиеся поднимают картинки, а также приводят свои примеры).
—Какие точки называются симметричными относительно точки О? (Точки A и B называются симметричными относительно точки O, если точка О является серединой отрезка AB).
— У вас на парте лежат фигуры. Поднимите те из них, которые имеют центр симметрии. (Круг, квадрат, шестиугольник).
—Приведите примеры центральной симметрии в окружающем мире. (Учащиеся поднимают картинки, а также приводят свои примеры).
2) Учащиеся в тетради чертят таблицу:
|
Предметы, обладающие симметрией |
Предметы, не обладающие симметрией |
Задание: предметы распределите по столбцам таблицы. (На листе изображения следующих предметов: звезда, имеющая оси симметрии, ель, имеющая ось симметрии, утюг, несимметричный дом, цветок).
Проверить правильность выполнения.
3) Тест «Симметрия» с последующей проверкой.
1) Если при сгибании плоскости чертежа по прямой, две фигуры совместятся, то такие фигуры называются с имметричными относительно прямой.
2) Если фигура некоторой прямой делится на две симметричные части, то ее называют симметричной относительно ____________________. Прямая, относительно которой симметричны части фигуры, называются осью симметрии.
3) Прямоугольник имеет 2 оси симметрии.
4) Квадрат имеет 4 оси симметрии.
5) Окружность имеет бесконечное множество осей симметрии.
6) Фигура называется центрально-симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.
7) Фигура ___________________ имеет центр симметрии.
8) Фигура___________________ имеет центр симметрии.
4) Работа с раздаточным материалом.
Учащимся выдается карточка с геометрическими фигурами.
Задание. Проведите оси симметрии фигур.
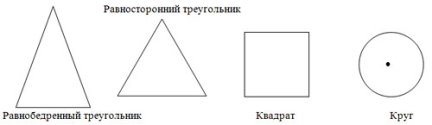
Рис. 1
Проверить правильность выполнения.
5) Повторение алгоритма построения точек, симметричных данным точкам относительно центра симметрии и оси симметрии.
—Как построить точку В, симметричную точке А относительно центра симметрии О? (Провести луч АО, на нем от т. О по другую сторону от т.А отложить отрезок ОВ, равный отрезку АО).
Задание . Построить треугольник MNK, симметричный треугольнику АВС относительно точки L.
Ученик выполняет задание на доске.
— Как построить точку В, симметричную точке А относительно прямой l? (Провести луч АМ, перпендикулярный прямой l и пересекающий прямую l в т. О. На этом луче от т. О и по другую сторону от т. А отложить отрезок ОВ, равный отрезку ОА).
Задание. Построить треугольник DEF, симметричный треугольнику АВС относительно прямой n.
Ученик выполняет задание на доске.
5 . Самостоятельная работа по вариантам. Работы сдаются учителю на проверку.
— Сейчас, когда мы повторили основные понятия темы, проведем самостоятельную работу.
Вариант 1
1) Смотрите задание на изображении.
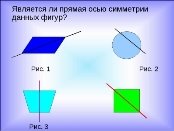
Рис. 2
2) Выпишите буквы русского алфавита, имеющие одну горизонтальную ось симметрии (см. рис. 3)

Рис. 3
3) Постройте фигуру, симметричную отрезку АВ относительно центра О.
Вариант 2
1) Смотрите задание на изображении.
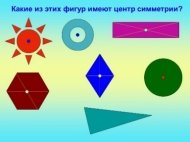
Рис. 4
2) Выпишите буквы, имеющие одну вертикальную ось симметрии (см. рис.3).
3) Постройте фигуру, симметричную отрезку СD относительно центра О.
6. Домашнее задание : № 1251, 1258, 1276 [1, с.261]
7. Подведение итогов урока .
Литература:
- Мерзляк А. Г., Полонский В. Б., Якир М. С. Математика 6 класс. -М.: Вентана-Граф, 2014. — 304 с.
- https://ds03.infourok.ru/uploads/ex/072f/0000b6f6–6d24e374/img15.jpg
- https://cloud.prezentacii.org/19/02/128420/images/screen15.jpg







