Методическая разработка интегрированного урока «Объём прямоугольного параллелепипеда»
Авторы: Бондарь Марина Александровна, Севастьянова Екатерина Леонидовна
Рубрика: Методическая копилка: конспекты и карты уроков
Опубликовано в Школьная педагогика №3 (22) октябрь 2021 г.
Дата публикации: 28.06.2021
Статья просмотрена: 156 раз
Библиографическое описание:
Бондарь, М. А. Методическая разработка интегрированного урока «Объём прямоугольного параллелепипеда» / М. А. Бондарь, Е. Л. Севастьянова. — Текст : непосредственный // Школьная педагогика. — 2021. — № 3 (22). — С. 22-26. — URL: https://moluch.ru/th/2/archive/204/6494/ (дата обращения: 26.04.2025).
В статье авторы пытаются определить взаимосвязь математики и английского языка.
Ключевые слова: объём прямоугольного параллелепипеда и куба, решение задач.
Целевые установки на достижение результата:
— личностные : формировать учебную мотивацию, необходимость приобретения новых знаний.
— метапредметные : формировать умение видеть математическую задачу в контексте проблемной ситуации, в других дисциплинах, развивать: логическое мышление, желание работать в коллективе, группе.
— предметные : обобщить знания обучающихся об объёме прямоугольного параллелепипеда, формировать умение применять формулы при решении задач, в том числе практико-ориентированных.
Структура и ход урока.
1) Организационный этап.
Здравствуйте, ребята! Я рада вас видеть и надеюсь, что сегодня на уроке нас ждёт и успех, и открытие. Будьте внимательны, думайте, делайте выводы, выдвигайте гипотезы, оценивайте себя и других и в тоже время умейте управлять своим поведением и своими знаниями.
Good morning, everybody. We’re glad to see you again. How are you? What’s the weather like today? How do you find it? To tell the truth, today we’re having an unusual lesson.
2)Постановка цели и задач урока. Мотивация учебной деятельности учащихся.
Начать урок мне хотелось бы со старой притчи: Let’s read it together: “The hungry and ragged man approached the fisherman and asked him to feed. The fisherman looked at him and said, «there lays the net, take it and take it to the sea». The man looked around, sighed, found the net and perplexed, carried to the sea. The fisherman followed him. They got in the boat and went out to sea. Man rowing at first failed, and then better and better, and finally he led the boat to the place where he was offered to stay. Then they threw the net and caught the fish. On the shore, the fisherman asked the man to gather dry branches, and together they kindled a fire. When the fish was ready, they ate, warmed up, rested. And then the man asked the fisherman, " Why didn't you give me the bread that you had in the cabin, and made me do all this?«The fisherman paused for a moment, and then said: «In this case, I would quench your hunger, but only once, and so I taught you to be eaten for a lifetime».
— В чём смысл этой притчи? Какое отношение она может иметь к нашему уроку?
Великий русский писатель Л. Н. Толстой писал: «Ум человеческий только тогда понимает обобщение, когда он сам его сделал или проверил».
— Какую тему мы проходили на прошлом уроке? Сегодня мы с вами продолжим работать по теме «Объём прямоугольного параллелепипеда».
— Какие цели вы себе сегодня ставите на уроке? (применять полученные знания о нахождении объёма параллелепипеда, видеть математическую задачу в контексте проблемной ситуации, в других дисциплинах, в окружающей жизни с применением иностранного языка)
3)Актуализация знаний.
Сегодня на уроке мы будем решать нестандартные задачи, проблемные задачи, практико-ориентированные задачи, задачи исследования, поработаем индивидуально, в парах, в группах, и в конце урока проведём самостоятельную работу и сделаем выводы.
—Поэтому начнем урок, как всегда с проверки домашней работы.
1) повторение определений и формул по теме: «Прямоугольный параллелепипед» и «Куб».
2) карточка в 2-х вариантах: Например:
- Прямоугольный параллелепипед — это ____; вершин_____; рёбер ____; граней______; три измерения ________; противоположные грани _________между собой; все грани — ________.
- S п.п. = _______?; L рёбер = ______-?, V пр.пар. =_______?
3) практическое задание: «Произвести измерения в кабинете математики № 71 следующим образом: 1-ый ряд измеряет длину класса; 2-ой ряд — ширину; 3-ий ряд — высоту классной комнаты».
4) Обобщение систематизация знаний. Подготовка учащихся к обобщенной деятельности. Воспроизведение на новом уровне.
Ребята, большую часть времени в школе мы проводим в учебных кабинетах. Именно поэтому к гигиеническому состоянию этих помещений предъявляются особо высокие требования. Несоблюдение гигиенических требований к воздушному режиму ухудшает восприятие и усвоение учебного материала. Основные нормы отражены в Санитарных правилах, утвержденных СанПиН. Комфортные, то есть физически хорошо воспринимаемые условия для учащихся в классах следующие: 18–20C°, атмосферное давление в среднем 760 мм ртутного столба, содержание 21 % кислорода, 0,04 % углекислого газа.
В классной комнате во время урока возрастает концентрация углекислого газа и падает содержание кислорода. Минимальная кубатура воздуха, приходящаяся на одного школьника достигает 3,75 м 3 . Возникает вопрос: Соответствуют ли размеры нашего класса и наполняемость его нормам СанПиН? Что для этого необходимо знать? Решим задачу и ответим на проблемный вопрос: соответствуют ли размеры кабинета нормам СанПиНа?
Дано: а=4,5м, b=6м, с=3,2 м., К=23 количество учащихся
Найти: V пр.пар. =? Решение: V пр.пар. =аbс, V=45дм×60дм×32дм= 86400дм 3 =86,4м 3 V 1 =3,75 м 3 , V:К=86,4м 3 :23=3,7м 3 Ответ: Размеры нашего класса и его наполняемость соответствуют нормам СанПиН.
5) Применение знаний и умений в новой ситуации.
Как вычислить объём следующих тел?
Найдите объём многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
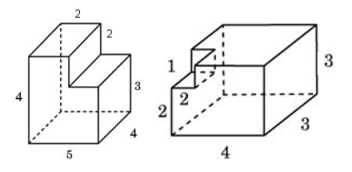
Например: Объём многогранника вычислим как объем прямоугольного параллелепипеда со сторонами 5, 4, 4 минус объём параллелепипеда со сторонами 2, 3, 4, получим: V=5×4×4–2×3×4 = 80–24 =56
Объём всего параллелепипеда равен V=4×3×3=36. Объём вырезанной части V 1 =2×1×1=2, следовательно, объём фигуры V — V 1 =36–2=34 [1].
Физминутка: Now it’s time to have a rest and do exercises:
Clap Your Hands
Clap, clap, clap your hands,
Clap your hands together.
Step, step, step your feet,
Step your feet together.
Touch, touch, touch your cheeks,
Touch your cheeks together.
Touch, touch, touch your ears,
Touch your ears together.
Shake, shake, shake your hands,
Shake your hands together.
Smile, smile at your friends,
Let us smile together.
6)Контроль усвоения, обсуждение допущенных ошибок и их коррекция.
Дифференцированная самостоятельная работа.
2 уровень
- Чему равно ребро куба, если объем равен 1000 куб.см.?
- Длина аквариума 80 см, ширина 45 см, а высота 55 см. Сколько литров воды надо влить в этот аквариум, чтобы уровень воды был ниже верхнего края аквариума на 10 см?
3 уровень
- Объем бассейна равен 100 м 3 , а стороны основания 10 м и 5 м. Сколько квадратных метров кафельной плитки ушло на облицовку бассейна?
- Из кирпичей, длина которых 30 см, ширина 10 см и высота 5 см, сложили куб, ребро которого равно 120 см. Сколько кирпичей на это было затрачено? [1].
7)Информация о д/з. Итог урока. Рефлексия.
Now you are supposed to estimate your partner’s activity at the lesson. Use this plan. Please, be polite.
—At the lesson he/she was active or passive.
—He/She is pleased or disappointed with the activity at the lesson.
—At the lesson he/she was tired or full of ideas and positive emotions.
—The lesson makes our mood better or worse.
—Some information was useful or useless, easy or difficult, interesting or uninteresting.
Welcome to here again! Thank for your attention and active work. Have a nice day!
Литература:
- Алгебра и начала математического анализа.11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни/ [С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин]. — 8-е изд. — М.: Просвещение, 2009.–464с.: ил. — (МГУ — школе).
Ключевые слова
решение задач, объём прямоугольного параллелепипеда и кубаПохожие статьи
Решение геометрических задач методом «Золотого сечения»
Данная статья посвящена обзору различных способов решения геометрических задач с помощью метода «золотого сечения». Рассмотрен математический термин «золотое сечение», его основные свойства.
Методическая разработка урока математики «Прямая пропорциональность и ее график»
В статье автор даёт описание урока математики в 7 классе.
Построение и применение треугольника Рело
В статье автор проводит изучение такого объекта как треугольник Рело. Изучаются различные варианты его построения и способы его использования в реальном мире.
Решение задач на тему «Квадратный трехчлен с параметрами»
В данной статье рассматриваются условия определенного расположения корней при помощи решения задач на квадратные трехчлены с параметрами.
Расстояние от точки до многогранника в пространстве
В данной работе рассмотрена задача поиска минимального расстояния между многогранником и точкой, не лежащей внутри него. Предложен алгоритм решения этой задачи и способ его применения в 3D-моделировании.
Разбиение многосвязного ортогонального полигона с минимизацией протяженности стыков на основе линейного программирования
Рассматривается задача разбиения многосвязного ортогонального полигона на прямоугольные области. Критерием оптимизации является минимизация протяженности стыков между прямоугольниками, образующими разбиение. Предложена модификация модели Бизли для ре...
Расчет площади поверхности сложных деталей
В работе осуществлен анализ способов измерения площади поверхности различных фигур. Представлен авторский метод расчета площади поверхности фигуры, как площади поверхности вращения с предварительным аналитическим описанием контура фигуры.
Алгебраические уравнения с параметром в углубленном курсе математики общеобразовательной школы
Актуальность выбранной темы обуславливается существующим на сегодняшний день противоречием между необходимостью обучения учащихся решению задач с параметрами в школьном курсе математики и фактической степенью развития методики обучения этой теме на п...
Анализ темы «Числовые последовательности» в учебных пособиях по алгебре
В статье автор проводит анализ темы «Числовые последовательности» в различных учебниках алгебры 9-го класса.
Применение вычислительного дизайна при разработке рационального очертания пространственной стержневой конструкции
В статье авторы рассматривают моделирование пространственной стержневой системы с помощью методов вычислительного дизайна. Исследуют применимость алгоритмического проектирования в задачах моделирования однослойных стержневых оболочек с треугольным де...
Похожие статьи
Решение геометрических задач методом «Золотого сечения»
Данная статья посвящена обзору различных способов решения геометрических задач с помощью метода «золотого сечения». Рассмотрен математический термин «золотое сечение», его основные свойства.
Методическая разработка урока математики «Прямая пропорциональность и ее график»
В статье автор даёт описание урока математики в 7 классе.
Построение и применение треугольника Рело
В статье автор проводит изучение такого объекта как треугольник Рело. Изучаются различные варианты его построения и способы его использования в реальном мире.
Решение задач на тему «Квадратный трехчлен с параметрами»
В данной статье рассматриваются условия определенного расположения корней при помощи решения задач на квадратные трехчлены с параметрами.
Расстояние от точки до многогранника в пространстве
В данной работе рассмотрена задача поиска минимального расстояния между многогранником и точкой, не лежащей внутри него. Предложен алгоритм решения этой задачи и способ его применения в 3D-моделировании.
Разбиение многосвязного ортогонального полигона с минимизацией протяженности стыков на основе линейного программирования
Рассматривается задача разбиения многосвязного ортогонального полигона на прямоугольные области. Критерием оптимизации является минимизация протяженности стыков между прямоугольниками, образующими разбиение. Предложена модификация модели Бизли для ре...
Расчет площади поверхности сложных деталей
В работе осуществлен анализ способов измерения площади поверхности различных фигур. Представлен авторский метод расчета площади поверхности фигуры, как площади поверхности вращения с предварительным аналитическим описанием контура фигуры.
Алгебраические уравнения с параметром в углубленном курсе математики общеобразовательной школы
Актуальность выбранной темы обуславливается существующим на сегодняшний день противоречием между необходимостью обучения учащихся решению задач с параметрами в школьном курсе математики и фактической степенью развития методики обучения этой теме на п...
Анализ темы «Числовые последовательности» в учебных пособиях по алгебре
В статье автор проводит анализ темы «Числовые последовательности» в различных учебниках алгебры 9-го класса.
Применение вычислительного дизайна при разработке рационального очертания пространственной стержневой конструкции
В статье авторы рассматривают моделирование пространственной стержневой системы с помощью методов вычислительного дизайна. Исследуют применимость алгоритмического проектирования в задачах моделирования однослойных стержневых оболочек с треугольным де...







