Методика работы над алгоритмической задачей
Авторы: Масленкова Валентина Александровна, Бондарева Яна Алексеевна, Васенина Анастасия Анатольевна
Рубрика: Методика преподавания учебных дисциплин
Опубликовано в Школьная педагогика №4 (7) ноябрь 2016 г.
Дата публикации: 06.11.2016
Статья просмотрена: 431 раз
Библиографическое описание:
Масленкова, В. А. Методика работы над алгоритмической задачей / В. А. Масленкова, Я. А. Бондарева, А. А. Васенина. — Текст : непосредственный // Школьная педагогика. — 2016. — № 4 (7). — С. 40-44. — URL: https://moluch.ru/th/2/archive/42/1546/ (дата обращения: 24.04.2025).
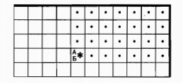
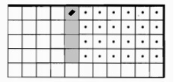
Приведём пример методики работы над алгоритмической задачей:
алг закрасить угол
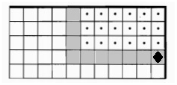
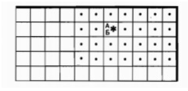
дано | робот внутри прямоугольника, огороженного стенами
надо | закрашены все клетки правее и выше стартовой, Робот в исходном положении
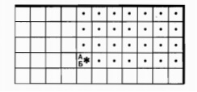
Разработка алгоритма совместно с учениками:
|
Вопросы, обобщение учителя |
Ожидаемые ответы |
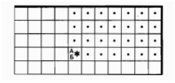
Обстановка (учитель на доске изображает начальную обстановку) |
|
Робот находится внутри прямоугольника, огороженного стенами |
|
|
1) Закрасить все пустые клетки выше стартовой; 2) Пойти вправо до стены; 3) Спуститься вниз на 3 клетки 4) Пойти влево и закрасить все пустые клетки; 5) Вернуться в исходное положение. |
|
|
Пока сверху свободно, закрасить |
|
|
Вверху прямоугольника у стены |
Ученик у доски закрашивает клетки
|
|
Пока справа свободно, вправо |
Ученик у доски закрашивает клетки
|
|
3 раза вниз |
Ученик у доски изображает место, где будет Робот
|
|
Нет, не будет |
|
|
Универсальный алгоритм |
|
|
1) Закрасить все клетки выше стартовой; 2) Вернуться в исходное положение; 3) Закрасить клетки правее стартовой; 4) Вернуться в исходное положение. |
|
|
Пока сверху свободно, закрасить |
Ученик у доски изображает место, где будет Робот
|
|
Пока клетка закрашена, вниз |
|
|
На одну клетку ниже исходного положения |
Ученик у доски изображает место, где будет Робот
|
|
Вверх |
Ученик у доски изображает место, где будет Робот
|
|
Пока справа свободно, закрасить |
Ученик у доски изображает место, где будет Робот
|
|
Около стены |
Ученик у доски изображает место, где будет Робот
|
|
Пока клетка закрашена, влево |
|
|
На одну клетку левее исходного положения |
Ученик у доски изображает место, где будет Робот
|
|
Вправо |
Ученик у доски изображает место, где будет Робот
|
|
Ученик у доски закрашивает клетки
|
|
|
Итак, идея нашего алгоритма: |
|
– Закрасить пустые клетки выше стартовой; – Вернуться в исходное положение; – Закрасить все клетки правее стартовой; – Вернуться в исходное положение. |
Модели частей алгоритма в форме блок-схем:
|
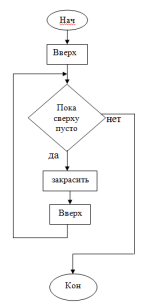
Давайте составим блок-схему для алгоритма закрашивания клеточек сверхуот Робота. Что мы делаем сначала? Шагаем вверх. Что идет дальше? Цикл «пока» Что пишется в ромбике? Условие Какое у нас условие? Пока сверху пусто Если условие выполняется? Закрашиваем клеточку, затем идем вверх Если условие не выполняется? Конец цикла Сколько раз выполнится условие? 3 раза (рис. 1). |
Рис. 1. Блок-схема для алгоритма закрашивания клеточек сверху от Робота |
|
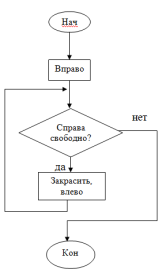
Давайте составим блок-схему для алгоритма закрашивания пустых клеток справаот Робота. Что мы делаем сначала? Шагаем вправо. Что идет дальше? Цикл «пока» Что пишется в ромбике? Условие Какое у нас условие? Пока справа свободно Если условие выполняется? Закрасить, вправо Если условие не выполняется? Конец цикла Сколько раз выполнится условие? 7 раз (рис.2). |
Рис. 2. Блок-схема для алгоритма закрашивания пустых клеток справа от Робота |
Задание для самостоятельной работы: составьте блок-схемы возвращения Робота в исходное положение.
Запись алгоритма решения задачи на алгоритмическом языке:

Проверка понимания алгоритма и правильности алгоритма:
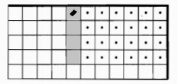
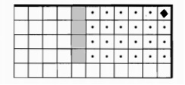
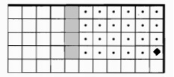
Как вы думаете, если Робот будет в другом положении, будет ли выполняться алгоритм? Проверьте на компьютере.
|
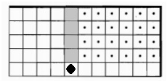
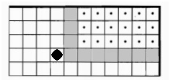
Вариант 1 |
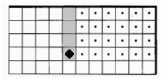
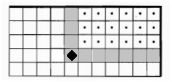
Вариант 2 |
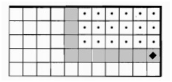
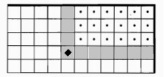
Вариант 3 |
|
|
|
|
Литература:
- «Информатика. 7-9 кл.»: Учебник для общеобразоват. учеб. заведений / А.Г. Кушниренко, Г.В. Лебедев, Я.Н. Зайдельман. — М.: Дрофа, 2001. — 336 с. https://www.niisi.ru/kumir/books.htm
- Федеральный государственный образовательный стандарт основного общего образования (5-9 кл.). 17.12.2010, № 1897; URL: http://минобрнауки.рф/документы/938.