Аксиоматические теории в курсе математической логики
Авторы: Сухан Ирина Владимировна, Кравченко Григорий Григорьевич, Иванисова Ольга Владимировна
Рубрика: Методика преподавания учебных дисциплин
Опубликовано в Педагогика высшей школы №3 (9) июль 2017 г.
Дата публикации: 13.06.2017
Статья просмотрена: 4120 раз
Библиографическое описание:
Сухан, И. В. Аксиоматические теории в курсе математической логики / И. В. Сухан, Г. Г. Кравченко, О. В. Иванисова. — Текст : непосредственный // Педагогика высшей школы. — 2017. — № 3 (9). — С. 28-39. — URL: https://moluch.ru/th/3/archive/64/2561/ (дата обращения: 19.12.2024).
В статье «К вопросу о методике изучения аксиоматического метода в курсе математической логики в вузе» [1] рассматривается история аксиоматического метода, а также концепция построения аксиоматических теорий. В данной статье будет рассмотрен вопрос построения формальных и неформальных аксиоматических теорий.
Появление парадоксов в теории множеств привлекло к вопросам оснований математики внимание практически всех ведущих математиков начала ХХ века. Была проделана большая работа по теоретико-множественному обоснованию математических и логических понятий. Основным итогом этой деятельности является становление математической логики как самостоятельной математической дисциплины, а принципиальным достижением математической логики — разработка современного аксиоматического метода.
Аксиоматические теории.
Современный аксиоматический метод содержит следующую концепцию аксиоматической теории.
Выбирается несколько первоначальных понятий, которые не определяются и используются без объяснения их смысла. Все другие понятия, которые будут использоваться, должны быть определены через первоначальные понятия и через понятия, смысл которых был определен ранее.
Затем выбирается несколько утверждений (высказываний, формул) о первоначальных и определяемых понятиях, эти утверждения объявляются истинными и называются аксиомами теории.
После этого, пользуясь правилами логического умозаключения, выводят новые утверждения о первоначальных и определяемых понятиях, которые называются теоремами.
Доказательством называется конечная последовательность высказываний (формул) теории w1, w2, …, wk, каждое из которых либо является аксиомой, либо выводится из одного или нескольких предыдущих высказываний (формул) этой последовательности по правилам вывода.
Теоремой называется высказывание (формула), являющееся последним в доказательстве.
Замечание. Любая аксиома является теоремой — доказательство состоит из одного шага.
Аксиоматической теорией называют систему из двух множеств высказываний (формул) T и W, таких, что T ⊂ W. МножествоWсостоит из всех высказываний (формул) данной теории, множество T состоит из доказуемых высказываний (формул) данной теории, называемых теоремами, выводимых из заданного множества высказываний (формул) To ⊂ W, называемых аксиомами.
Таким образом, To ⊂ T ⊂ W.
Основными свойствами аксиоматических теорий являются непротиворечивость иполнота.
Непротиворечивость теории означает невозможность вывода в данной теории некоторой формулы и ее отрицания.
Полнота теории означает возможность вывода для любой формулы либо самой этой формулы, либо ее отрицания.
В математической логике рассматривают неформальные и формальные аксиоматические теории.
Неформальные аксиоматические теории служат для построения содержательных математических теорий (геометрия, арифметика, теория вероятностей, теоретическая механика и т. п.). Правила вывода в неформальную аксиоматическую теорию не включаются — используется какая-либо известная система логических правил вывода.
Формальные аксиоматические теории рассматривают, если предметом изучения является некоторая математическая теория. Правила вывода включаются в формальную аксиоматическую теорию.
Таким образом, в неформальных аксиоматических теориях изучаются формальные объекты (числа, точки, прямые, множества и т. п.), однако при применении логических правил вывода рассуждают содержательно, а не формально. Например, считается известным и понятным смысл слов: «утверждение А противоречит утверждению В» или «из утверждения А следует утверждение В».
В формальных аксиоматических теориях делается следующий шаг на пути формализации аксиоматических теорий, состоящий в формализации процессов построения умозаключений (логических следствий).
Неформальные аксиоматические теории.
При построении неформальной аксиоматической теории обычно исходят из некоторой достаточно развитой интуитивной теории и предполагают известной систему формальной классической логики. В качестве примеров можно привести такие теории, как арифметика, геометрия, механика, теория вероятностей.
После того, как интуитивная теория развита настолько, что ее основные свойства считаются известными, можно попытаться ее аксиоматизировать.
Первым шагом в построении неформальной аксиоматической теории является составление перечня объектов данной теории S0ивыбор символов для их обозначения. Эти символы называются первичными терминами или первичными символами.
Вторым шагом в построении неформальной аксиоматической теории является составление перечня основных свойств T0 отобранных объектов, то есть высказываний об основных объектах, и запись их при помощи первичных символов. Эти свойства называются аксиомами.
Упорядоченная пара множеств
Далее, следуя принятой системе логики, выводят из аксиом теоремы, то есть строят множество T. Очевидно, что принадлежность определенной формулы множеству T связана с тем, на какой системе логики основывается данная теория.
Первичные термины неформальных аксиоматических теорий не определяются, перечисляются только их свойства в виде аксиом.
Обычно при построении неформальных аксиоматических теорий в качестве первичных терминов берутся некоторые множества. Это означает, что при построении таких неформальных аксиоматических теорий предусматривается некоторая аксиоматизация теории множеств, позволяющая затем определять эти теории посредством теоретико-множественных предикатов.
При построении неформальной аксиоматической теории предполагается, что значения (смысл) первичных символов определяются соответствующей интуитивной теорией. Однако, после того, как теория построена, входящие в нее первичные термины могут быть наделены новым смыслом, то есть им могут быть приписаны другие значения.
Интерпретацией неформальной аксиоматической теории называется приписывание значений (смысла) первичным терминам теории.
Моделью неформальной аксиоматической теории называется совокупность объектов, выбранных в качестве ее интерпретации, удовлетворяющих аксиомам теории.
Пример неформальной аксиоматической теории.
Первичные термины: непустое множество G, бинарная операция, элемент e∊G, то есть S0 = {G, ∙, e∊G}.
Аксиомы:
G1.∀a∊G, ∀b∊G: ∃!a∙b∊G.
G2. ∀a∊G, ∀b∊G: a∙(b∙c) = (a∙b)∙c.
G3. ∀a∊G: a∙e = e∙a = a.
G4. ∀a∊G, ∃a’∊a: a∙a’ = a’∙a = e.
То есть T0 = {G1, G2, G3, G4}.
Эта неформальная аксиоматическая теория называется теорией групп.
Примеры моделей теории групп:
− множество целых чисел с операцией сложения и числом 0 в качестве e;
− множество R+ = (0; +∞) с операцией умножения и числом 1 в качестве e;
− множество всех подмножеств любого непустого множества с операцией симметрической разности и множеством ∅вкачестве e.
Неформальная аксиоматическая теория называется непротиворечивой, если она не содержит такого высказывания A, что A и ¬A являются теоремами.
Неформальная аксиоматическая теория называется противоречивой, если она содержит такое высказывание A, что A и A являются теоремами.
Противоречивые теории не имеют смысла так, как если в используемую систему логики входит правило отделения: A, A → B |=B, то можно доказать, что любая формула такой теории является теоремой.
Действительно, пусть C — любое высказывание противоречивой теории, содержащей теоремы A и A. Используя тавтологию A → (A → C)получаем: A, A → (A → C) |= A → C,далее получаем:A, A → C |= C.
Для неформальных аксиоматических теорий вопрос о непротиворечивости может быть решен с помощью модели. Если теория противоречива, то любая ее модель содержит противоречие, так как пара противоречащих теорем переводится в два противоречащих высказывания о модели.
Если для неформальной аксиоматической теории можно найти такую интерпретацию, что T является конечным множеством, то отсутствие противоречивости можно проверить непосредственно.
Например, теория групп непротиворечива, так как ее моделью служит одноэлементное множество {e}соперацией e∙e = e.
Если теория имеет только бесконечные модели, то установление непротиворечивости с помощью модели носит относительный характер, то есть теория непротиворечива, если непротиворечива модель. Например, геометрия Лобачевского непротиворечива, если непротиворечива геометрия Евклида.
Непротиворечивость геометрии Евклида, как и непротиворечивость практически всех классических математических теорий, сводится к непротиворечивости арифметики натуральных чисел.
Проблему полноты для неформальных аксиоматических теорий не рассматривают, так как ответ на вопрос о том, является ли некоторая формула неформальной аксиоматической теории теоремой или нет, может зависеть от выбора системы логических правил вывода.
Формальные аксиоматические теории.
При изложении содержательных математических теорий широко используются символы, которые заменяют некоторые математические объекты (точки, прямые, числа, вектора, матрицы, функции и т. п.).
В отличие от обычного употребления символов в математике, в формальных аксиоматических теориях символы не заменяют собой никаких других объектов. Символы в формальных аксиоматических теориях трактуются как значки, с которыми обращаются согласно определенным правилам, зависящим лишь от формы выражений, образованных из символов.
Для построения формальной аксиоматической теории используется формальный язык теории.
Алфавитом A(T)формальной аксиоматической теории называется непустое конечное множество символов, называемых буквами.
Словом или выражением валфавитеA(T)называется любая конечная последовательность букв.
Формальным языком формальной аксиоматической теории называется пара
Формулами вформальной аксиоматической теории являются последовательности символов определенного вида, то есть не всякое слово (выражение) является формулой данной формальной аксиоматической теории.
Из множества формул выделяется некоторое подмножество формул, называемых аксиомами.
Задается конечное множество отношений между формулами, называемых правилами вывода.
Выводом в формальной аксиоматической теории называется конечная последовательность формул этой теории B1, B2, …, Bn, каждая из которых либо является аксиомой, либо выводится из одной или нескольких предыдущих формул этой последовательности по одному из правил вывода.
Формула Ф формальной аксиоматической теории называется теоремой, если существует вывод, последней формулой которого является Ф.
Замечание. Любая аксиома является теоремой — вывод состоит из одной формулы.
При построении формальных аксиоматических теорий используется понятие эффективной процедуры (или эффективного алгоритма).
Под эффективной процедурой понимается совокупность предписаний, позволяющая посредством формального выполнения этих предписаний за конечное число шагов получить ответ на любой вопрос из некоторого класса вопросов.
Для формальной аксиоматической теории должны выполняться следующие требования:
− понятие формулы должно быть эффективным, то есть должна существовать эффективная процедура, позволяющая для произвольной строчки символов решить, является ли она формулой;
− понятие аксиомы должно быть эффективным, то есть должна существовать эффективная процедура, позволяющая для произвольной формулы решить, является ли она аксиомой;
− понятие вывода должно быть эффективным, то есть должна существовать эффективная процедура, позволяющая для произвольной конечной последовательности формул решить, может ли каждый член этой последовательности быть выведен из одной или нескольких предшествующих формул этой последовательности посредством правил вывода.
Формальные аксиоматические теории в математической логике принято называть исчислениями.
Пример формальной аксиоматической теории
Простым примером формальной аксиоматической теории является исчисление высказываний, которое можно определить следующим образом.
Алфавит исчисления высказываний содержит:
- Символы: ¬, →, (,).
- Буквы и буквы с нижним индексом: A,B,C, …, A1, B1, C1….
Формулы исчисления высказываний определяются следующим образом:
- A, B, C, …, A1, B1, C1… — формулы.
- Если A формула, то ¬(A) — формула.
- Если A иBформулы, то (A) → (B) — формула.
- Строчка символов является формулой, только если она удовлетворяет условиям 1–3.
Аксиомы исчисления высказываний.
Для любых формул A, B и C следующие формулы являются аксиомами:
1) (A → (B → A)).
2) ((A → (B → C)) → ((A → B) → (A → C)).
3) ((¬B → ¬A) → ((¬B → A) → B)).
Правило вывода: из A и A → B следует B.
Доказано, что исчисление высказываний является полной и непротиворечивой формальной аксиоматической теорией.
Для формализации рассуждений, которые не могут быть обоснованы в рамках исчисления высказываний, в математической логике используют исчисление предикатов.
Язык исчисления предикатов содержит:
- Конечное или счетное множество предметных постоянных {a1, a2, …}.
- Конечное или счетное множество предметных переменных {x1, x2, …}.
-
Конечное или счетное множество предикатных букв
-
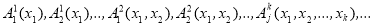
Конечное или счетное множество функциональных букв
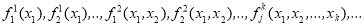
- Логические связки ¬, →, символ квантора ∀, скобки (,) и запятую.
Верхний индекс предикатной или функциональной буквы указывает число аргументов, а нижний индекс служит для различения букв с одним и тем же числом аргументов.
Аргументами функциональных букв и результатом их применения являются термы.
Термы определяются следующим образом:
- Предметная переменная или предметная постоянная — терм.
-
Если t1, t2, …, tn — термы, то
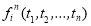— терм.
- Строчка символов является термом, только если она удовлетворяет условиям 1 и 2.
Аргументами предикатных букв являются термы. Результатом применения предикатных букв являются элементарные формулы: если 
— предикатная буква, а t1, t2,…,tn — термы, то 
— элементарная формула.
Формулы исчисления предикатов определяются следующим образом:
- Любая элементарная формула —формула.
- Если A формула, то ¬(A) — формула.
- Если A иBформулы, то (A) → (B) — формула.
- Если A — формула, а x — предметная переменная, то ∀x A — формула. При этом формула A называется областью действия квантора ∀x.
- Строчка символов является формулой, только если она удовлетворяет условиям 1–4.
Вхождение переменной x в формулу называется связанным, если x является переменной входящего в эту формулу квантора ∀xили находится в области действия входящего в эту формулу квантора ∀x,впротивном случае вхождение переменной x в данную формулу называется свободным.
Переменная называется свободной переменной вформуле, если существуют свободные ее вхождения в эту формулу.
Переменная называется связанной переменной вформуле, если существуют связанные ее вхождения в эту формулу.
Таким образом, переменная может быть одновременно свободной и связанной в одной и той же формуле.
Терм t называется свободным для переменной xiвформуле A,если никакое свободное вхождение xi в Aне лежит в области действия никакого квантора ∀xj,гдеxj — переменная, входящая в t.
Пример. Терм 
свободен для x1в 
, но несвободен для x1в 
.
Интерпретацией языка формальной аксиоматической теории называется соответствие, сопоставляющее каждому элементу языка теории единственный элемент некоторого множества D,называемого областью интерпретации.
При этом каждой предикатной букве 
соответствует некоторое n-местное отношение в D, каждой функциональной букве 
— некоторая n-местная операция в D(то есть функция, отображающая DnвD), каждой предметной постоянной ai — некоторый элемент из D.
При интерпретации предметные переменные принимают значения из области D, логические связки и кванторы имеют обычный смысл.
При интерпретации всякая формула формальной аксиоматической теории без свободных переменных представляет собой высказывание, которое или истинно или ложно, а всякая формула со свободными переменными представляет некоторое отношение на области интерпретации, которое для одних значений истинно, а для других ложно.
Пример. Если в качестве области интерпретации взять множество целых положительных чисел, а формулу 
интерпретировать как отношение x1 ≤ x2, то 
истинно для всех упорядоченных пар (a, b) целых положительных чисел таких, что a ≤ b.
В этой интерпретации формула 
представляет собой свойство (то есть отношение с одним аргументом) «для каждого целого положительного x2: x1 ≤ x2» которое выполняется только для числа 1, а формула 
является истинным высказыванием, утверждающим существование наименьшего целого положительного числа, то есть 1.
Моделью формальной аксиоматической теории называетсяинтерпретация языка формальной аксиоматической теории, в которой истинны все аксиомы теории.
Например, моделью исчисления высказываний является алгебра высказываний.
Формальные аксиоматические теории первого порядка.
Для формализации математических теорий в математической логике используют формальные аксиоматические теории первого порядка, в которых не допускаются предикаты, имеющие аргументами предикаты и функции, а также не допускаются кванторы по предикатам и функциям.
Язык формальной аксиоматической теории первого порядка совпадает с языком исчисления предикатов. Термы и формулы теории первого порядка определяются также как и в исчислении предикатов.
Аксиомы теории первого порядка разбивают на два класса: логические аксиомы исобственные (нелогические) аксиомы.
Перечни логических аксиом и правил вывода теорий первого порядка это дополненные соответствующие перечни исчисления высказываний.
Логические аксиомы теории первого порядка.
Для любых формул A, B и C следующие формулы являются аксиомами:
- (A → (B → A)).
- ((A → (B → C)) → ((A → B) → (A → C)).
- ((¬B → ¬A) → ((¬B → A) → B)).
- ∀xi A(xi) → A(t),гдеt — терм, свободный для xiвформуле A(xi).
- ∀xi (A → B) → (A → ∀xi B),если формула A не содержит свободных вхождений xi.
Собственные аксиомы не могут быть сформулированы в общем случае и меняются от теории к теории.
Правила вывода:
- Из A и A → B следует B.
- Из A следует ∀xi (A).
Теория первого порядка, не содержащая собственных аксиом, называется исчислением предикатов первого порядка.
Доказано, что исчисление предикатов первого порядка является полной и непротиворечивой теорией.
Моделью исчисления предикатов первого порядка является логика предикатов.
Пример теории первого порядка содержащей собственные аксиомы.
Теория имеет одну предикатную букву 
, одну функциональную букву 
и одну предметную константу a1.
В соответствии с общепринятыми обозначениями будем писать t = s вместо 
, t + s вместо 
и 0вместо a1.
Собственными аксиомами теории являются формулы:
- ∀x1∀x2∀x3 (x1 + (x2 + x3) = (x1 + x2) + x3).
- ∀x1 (0 + x1 = x1).
- ∀x1∃x2 (x2 + x1 = 0).
- ∀x1(x1 = x1).
- ∀x1∀x2 ((x1 = x2) → (x2 = x1))
- «x1«x2«x3 ((x1 = x2) → ((x2 = x3) → (x1 = x3))).
- «x1«x2«x3 ((x2 = x3) → ((x1 + x2 = x1 + x3) (x2 + x1 = x3 + x1))).
Всякая модель этой теории называется группой.
Если в группе истинна формула ∀x1∀x2 (x1 +x2 = x2 + x1), то группа называется абелевой, или коммутативной.
В качестве моделей теории групп, как теории первого порядка, можно взять, например, модели, приведенные для теории групп, как неформальной аксиоматической теории:
− множество целых чисел с операцией сложения и числом 0 в качестве 0;
− множество R+ = (0; +∞) с операцией умножения и числом 1 в качестве 0;
− множество всех подмножеств любого непустого множества с операцией симметрической разности и множеством ∅вкачестве 0.
Метаматематика.
Язык, на котором дается описание какой-либо формальной аксиоматической теории, называется метаязыком.
Соотношение между метаязыком и формальным (предметным) языком формальной аксиоматической теории примерно такое же, как соотношение между русским и французским языками с точки зрения человека, изучающего французский язык и владеющего русским языком. Все начальные сведения и пояснения в словарях и учебниках учащийся получает на русском языке (на метаязыке), впоследствии же он начинает писать и говорить по-французски (на предметном языке).
В качестве метаязыка можно использовать некоторый узкий фрагмент какого-либо национального языка, например, русского. Если разрешить использовать в качестве метаязыка весь национальный язык, то возникает опасность вывода парадоксов — например, парадокса Рассела.
Теоремы, описывающие какие-либо свойства формальной аксиоматической теории, называются метатеоремами.
Метатеоремы следует отличать от теорем соответствующей формальной аксиоматической теории. Теоремы формальной аксиоматической теории записываются на формальном языке формальной аксиоматической теории, а метатеоремы — на метаязыке.
Например, A → A — теорема исчисления высказываний, а «Исчисление высказываний непротиворечиво» — метатеорема.
Для доказательства метатеорем допускаются только бесспорныесредства обычной логики, так например, должны быть исключены доказательство от противного, а также доказательства, апеллирующие к бесконечному множеству операций над формулами. Доказательства метатеорем существования должны быть конструктивными — для объекта, существование которого утверждается, должен быть указан метод его построения.
Изучение формальных аксиоматических теорий с использованием логических средств, соответствующих указанным ограничениям, называется метаматематикой.
Заинтересованный читатель может глубже ознакомиться с этими вопросами, обратившись к [2, 3, 4, 5, 6].
Литература:
- Сухан И. В., Кравченко Г. Г., Иванисова О. В. К вопросу о методике изучения аксиоматического метода в курсе математической логики в вузе. // Педагогика высшей школы. — 2016. — № 3. — С. 125–128.
- Успенский В. А., Верещагин Н. К., Плиско В. Е. Вводный курс математической логики. — М.: Физматлит, 2007. — 128 с.
- Игошин В. И. Математическая логика и теория алгоритмов. — М.: Издательский центр «Академия», 2010. — 448 с.
- Колмогоров А. Н., Драгалин А. Г. Введение в математическую логику. — М.: Издательство Московского университета, 1982. — 120 с.
- Мендельсон Э. Введение в математическую логику. — М.: Наука, 1976. — 320 с.
- Столл Р. Р. Множества. Логика. Аксиоматические теории. — М.: Просвещение, 1968. — 232 с.
