Круги Эйлера в курсе математики 6–9-х классов
Автор: Сычева Ирина Александровна
Рубрика: Общеобразовательная школа
Опубликовано в Образование и воспитание №1 (47) февраль 2024 г.
Дата публикации: 31.01.2024
Статья просмотрена: 231 раз
Библиографическое описание:
Сычева, И. А. Круги Эйлера в курсе математики 6–9-х классов / И. А. Сычева. — Текст : непосредственный // Образование и воспитание. — 2024. — № 1 (47). — С. 12-14. — URL: https://moluch.ru/th/4/archive/262/8963/ (дата обращения: 24.04.2025).
Круги Эйлера представляют собой геометрическую схему для наглядного изображения отношений между определенным множеством и его частью. Благодаря наглядности они значительно упрощают решение многих задач. Автором метода кругов считается Леонард Эйлер — швейцарский, прусский и русский математик.
Позже круги Эйлера использовали в своих работах такие известные ученые, как: Бернард Больцано, Эрнест Шредер, Джон Венн и другие.
Сегодня круги Эйлера являются одним из основных методов для развития логического мышления, для подготовки и решения олимпиадных задач. В данной статье рассматриваются задачи с 2 и 3 кругами Эйлера, а также, дается общая формула для решения этих задач.
Задача № 1: В классе 30 учащихся. Из них 25 учеников любят математику, 14 любят физику. Сколько человек одновременно любят физику и математику.
Решение:
I способ
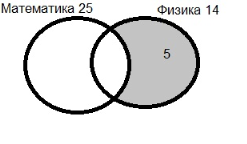
1) 30–25 = 5 (уч.) не любят математику, т. е. любят только физику
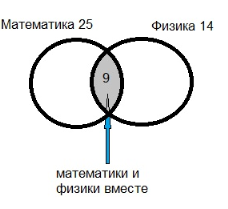
2) 14–5 = 9 (уч.) любят математику и физику вместе
Ответ: 9 учеников любят одновременно и математику, и физику.
II способ:
1) 30–14 = 16 (уч.) не любят физику, т. е. любят только математику
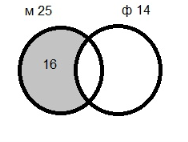
2) 25–16 = 9 (уч.) любят математику и физику одновременно.
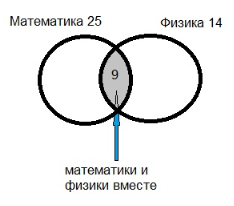
Ответ: 9 учеников любят одновременно и математику и физику.
III способ:
Пусть х учеников любят и математику, и физику одновременно, тогда х=9 человек.
25+14-х = 30
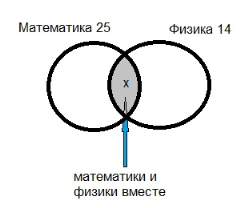
Ответ: 9 учеников любят одновременно и математику и физику.
Можно вывести формулу для нахождения общего числа элементов пересекающихся множеств.
Пусть х — элементы первого множества, а у — элементы второго множества.
Тогда пересечение z — общие элементы множества х и у.
Общее число всех элементов в двух кругах
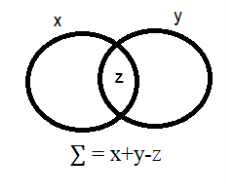
Задача № 2: Из 100 семей 75 имеют дачи, 87 семей имеют квартиры, 9 семей совсем не имеют недвижимости. Сколько семей имеют и дачи и квартиры.
Решение:
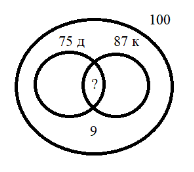
1) 100–9 = 91 (с.) имеют хотя бы какую-то недвижимость, т. е. дачу или квартиру, или дачу и квартиру
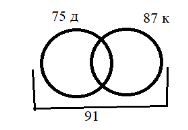
2) 91–75=16 (с.) имеют только квартиры
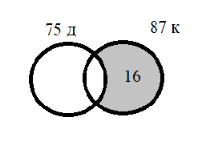
3) 87–16=71 (с.) имеют и дачу и квартиру
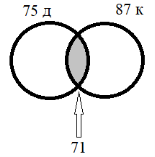
Ответ: 71 семья имеет в собственности и дачу и квартиру.
Рассмотрим операции с тремя кругами.
Задача № 3: 100 ребят уехали в спортивный лагерь.
30 ребят умеют кататься на велосипеде
28 ребят занимаются борьбой
42 ребенка занимаются гимнастикой
8 ребят занимаются борьбой и умеют кататься на велосипеде
5 ребят умеют кататься на велосипеде и занимаются гимнастикой
10 ребят занимаются и борьбой и гимнастикой
3 ребенка умеют кататься на велосипеде, занимаются и борьбой и гимнастикой.
Сколько ребят ничего не умеют (ни ездить на велосипеде, ни занимаются борьбой, ни занимаются гимнастикой).
Решение:
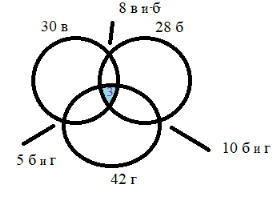
1) 8–3 = 5 (р.) умеют ездить на велосипеде и занимаются борьбой, но не занимаются гимнастикой.
2) 5–3 = 2 (р.) велосипедисты и гимнасты, но не занимаются борьбой
3) 10–3 = 7 (р.) занимаются борьбой и гимнастикой, но не умеют кататься на велосипеде
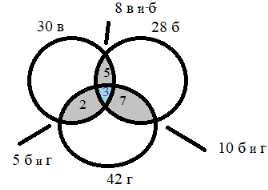
4) 30–5–3–2 = 20 (р.) только умеют кататься на велосипеде
5) 28–5–3–7 = 13 (р.) занимаются только борьбой
6) 42–2–3–7 = 30 (р.) занимаются только гимнастикой
7) 30+20+30 = 80 (р.) занимаются каким-то спортом (или гимнастикой, или борьбой или умеют кататься на велосипеде)
8) 100–80 = 20 (р.) не занимаются ничем
Ответ: 20 ребят ничего не умеют, ни кататься на велосипеде, ни занимаются гимнастикой, ни занимаются борьбой.
Можно вывести формулу для трех множеств и решать такие задачи без рисунка с кругами Эйлера.
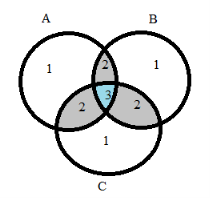
Пусть n (A) — количество элементов в множестве А
n (В) — количество элементов в множестве В
n (С) — количество элементов в множестве С
Общее количество объектов в трех кругах
∑ = n(A) + n(B) + n(C) — n(A∩B) — n(A∩C) — n(B∩C) + n(A∩B∩C)
Посчитаем общее количество элементов из условия предыдущей задачи:
n(A) = 30
n(B) = 28
n(C) = 42
n(A∩B) = 8
n(B∩C) = 10
n(A∩C) = 5
n(A∩B∩C) = 3
∑ = 30+28+42–8–10–5+3 = 80







