Дифференцированное обучение математике в 5 классе на примере геометрического материала
Автор: Ракитина Анна Дамировна
Рубрика: Спецвыпуск
Опубликовано в Образование и воспитание №2 (48) апрель 2024 г.
Дата публикации: 27.02.2024
Статья просмотрена: 24 раза
Библиографическое описание:
Ракитина, А. Д. Дифференцированное обучение математике в 5 классе на примере геометрического материала / А. Д. Ракитина. — Текст : непосредственный // Образование и воспитание. — 2024. — № 2 (48). — С. Т.1. 20-21. — URL: https://moluch.ru/th/4/archive/266/9030/ (дата обращения: 05.04.2025).

Современный этап российского образования характеризуется её направленностью на дифференциацию, как профильную — на старшей ступени обучения, так и уровневую — в основной и старшей школе. Дифференциация школьного образования имеет, прежде всего, другую иерархию целей учебно-воспитательного процесса. Если раньше приоритет всегда отдавался образовательным целям, то сегодня на первый план выступают воспитательные и развивающие цели. В обучении математике делается перенос акцента с «математического образования» на «образование с помощью математики», позволяющего более эффективно решить проблему формирования личности обучающегося, его интеллектуального потенциала, подготовку творчески мыслящего человека. Под дифференциацией обучения, согласно В. А. Гусеву мы будем понимать учебно-воспитательный процесс, протекающий с учетом доминирующих особенностей групп учащихся [1].
Изучение геометрического материала в 5 классе — это продолжение работы, начатой в начальных классах, а также пропедевтический курс геометрии. В этом классе изучаются основные понятия курса геометрии, которые потом уточняются и углубляются.
В процессе обучения геометрии в 5 классе можно и нужно осуществлять дифференциацию обучения. Рассмотрим этот подход на примере тем «Площади фигур», «Объёмы. Объём прямоугольного параллелепипеда».
Как отмечают исследователи [2, 3] необходимо учитывать, что дифференциация должна осуществляться за счёт задачного материала, а не за счёт содержания обучения. При этом для повышения познавательного интереса у учащихся рекомендуем использовать практико-ориентированные задачи (задачи, моделирующие реальную или близкую к реальной ситуацию). Например, вычислить объём спичечной коробки или найти площадь поверхности кабинета. На уроках математики успешно применяются модели многогранников, которые можно дифференцировать по сложности фигуры для развития пространственного воображения (см. рис. 1). На этих моделях обучающимся предлагается вычислить объём и площадь поверхности фигуры.
Урок по теме «Объёмы. Объём прямоугольного параллелепипеда» можно провести в виде практической работы с использованием моделей, изготовленных заранее для каждого ученика. При выполнении данной практической работы учитель проводит инструктаж: «Сейчас все выполняют задание № 1, тем, кто справится с заданием, ставится оценка «3». Чтобы получить «4» — выполните № 1 и № 2, а для оценки «5» требуется решить все задания».
Для развития графической культуры обучающихся предлагаются задания: изобразить трёхмерную фигуру в тетради, сделать развёртку простейших многогранников, вычислить объём фигур.
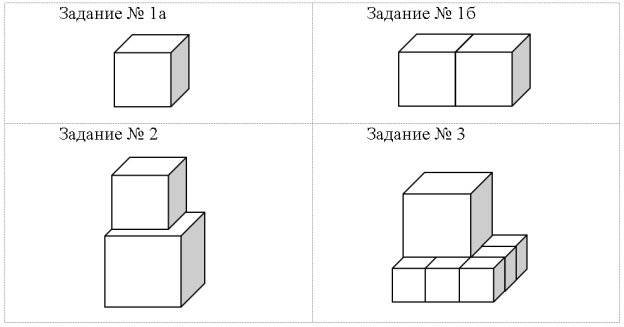
Рис. 1. Примеры моделей
При дифференцированном обучении нужно дать возможность каждому ученику попробовать решить задачи сложного уровня, а обучающиеся с математическими способностями должны не только уметь решать олимпиадные задания, но и безошибочно справляться с задачами базового уровня. Выполнение каждой практической работы все учащиеся начинают с базового уровня, далее при успешном прохождении данного уровня ученик допускается на следующий.
Литература:
- Гусев В. А. Индивидуализация учебной деятельности учащихся как основа дифференцированного обучения математике в средней школе// Математика в школе. 1990. № 4. С.27–31.
- Индивидуализация и дифференциация в педагогической теории и практике (анализ отечественного опыта) / А. Ж. Жафяров, Е. С. Никитина, М. Е. Федотова. Новосибирск: Изд-во НГПУ, 2004, 36с.
- Унт И. Э. Индивидуализация и дифференциация обучения. М.: Педагогика, 2010. 192с.







