Универсальные рекурсивные алгоритмы в подготовке школьников к ЕГЭ и ОГЭ по информатике: опыт методического исследования
Автор: Мартьянов Евгений Юрьевич
Рубрика: Общеобразовательная школа
Опубликовано в Образование и воспитание №4 (50) октябрь 2024 г.
Дата публикации: 27.09.2024
Статья просмотрена: 10 раз
Библиографическое описание:
Мартьянов, Е. Ю. Универсальные рекурсивные алгоритмы в подготовке школьников к ЕГЭ и ОГЭ по информатике: опыт методического исследования / Е. Ю. Мартьянов. — Текст : непосредственный // Образование и воспитание. — 2024. — № 4 (50). — С. 11-14. — URL: https://moluch.ru/th/4/archive/272/9434/ (дата обращения: 24.04.2025).
Статья представляет собой опыт методического исследования проблемы «шаблонов» при подготовке к экзаменам по информатике. Приводятся примеры шаблонных решений, рассматривается их эволюция, автор представляет шаблонные решения как универсальные алгоритмы, рассматривая их связь с фундаментальными понятиями структур данных.
Ключевые слова: информатика егэ огэ, шаблон, рекурсия.
В научном и методическом сообществе о «шаблонных» методах решения задач говорят негативно. Под понятием «шаблон» понимается упрощённое наивное решение, логика которого легко ломается малейшим изменением сюжета и условия задачи. Подобная трактовка значительно упрощает понимание словарной дефиниции — «образца для решения прикладных задач». Обратимся к практике: в 2023 году из ЕГЭ по информатике было исключено задание № 13 на поиск оптимального пути/количества путей в ориентированном графе. Универсальный метод решения данного задания активно популяризировал А. М. Кабанов в своих работах. [1] Основная идея заключается в том, что решения задачи пишется небольшая функция, которая изменяется лишь незначительно в зависимости от условия задачи. Рассмотрим конкретный пример задания (рис. 1).
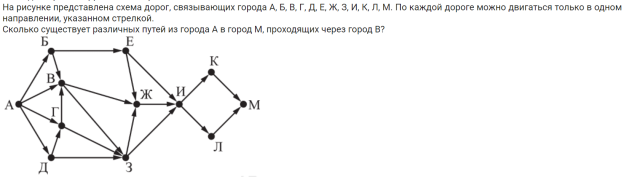
Рис. 1.
Решение данной задачи шаблоном реализуется в 6 строк кода рекурсивным алгоритмом. Основная идея заключается в том, чтобы перенести ориентированный граф в синтаксическую структуру словаря, а затем выполнять рекурсивный проход по значениям словаря от ключа последней буквы текущей строки. Изобразим схему идеи (рис. 2).
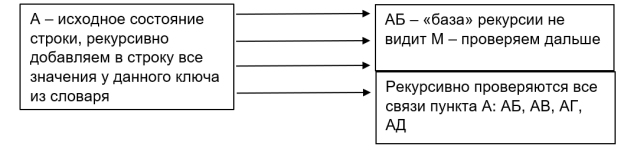
Рис. 2
Таким образом, программа рекурсивно подсчитывает все искомые пути в задаче. Пример реализации программного кода на языке программирования Python представлен на рис. 3.

Рис. 3
Данная программная реализация является отличным примером классического «шаблона» в плане универсального подхода к решению задач на ориентированный граф. Образец имеет варианты гибкой настройки. К примеру, условие задачи с обязательным посещением пункта В реализовано в строке № 3, в логическое условие and возможно добавлять и сложные условия в несколько пунктов обязательных или, наоборот, избегаемых к посещению. Для дополнительной наглядности возможно добавить вывод всех путей в консоль, дописав в условие перед строкой № 4 — print (c). Если условие задачи требует, чтобы пункты посещались только 1 раз в генератор sum строки № 5 требуется добавить условие: if c.count(x)<=1.
Таким образом, шаблон решения задачи предусматривает варианты решения любого прототипа задачи с незначительным изменением основной идеи кода. Разработка данного универсального решения значительно сказалась на положении задачи в актуальном банке заданий ЕГЭ. В демоверсии 2023 года разработчики значительно усложнили задачу, добавив в неё идею цикличных путей. Однако же, представленное решение оказалось настолько выгодным, что решало и новый прототип задания с незначительным усложнением кода.
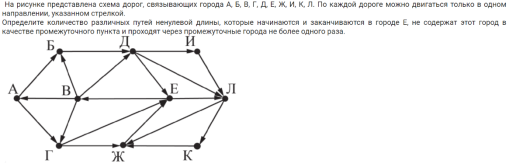
Рис. 4.
Идея усложнения заключается в том, что использование стандартного шаблона учеником приведёт к ответу 1, так как граф цикличен. (возможные пути, по условию, начинаются и заканчиваются в городе Е, рекурсия будет завершаться сразу) Однако, несложно реализовать в шаблоне идею о том, что подсчёт суммы дорог начинающихся в пунктах, связанных с Е и оканчивающихся в Е приведёт к правильному ответу.

Рис. 5.
В третьей строке условие включает в себя «e not in c [1:-1]», — проверяется условие, что пункт Е не может находиться в любой другой позиции, кроме начала и конца строки. Внутри функции print() развёрнут генератор sum(),который суммирует все пути по условию из пунктов-значений словаря d с ключом «Е». Таким образом, суммировав пути, которые выходят из пункта Г и заканчиваются в Е, то же и с Ж, мы получаем правильный ответ.
Идея «цикличных дорог» стала последним усложнением разработчиками 13 задания ЕГЭ. Высокий процент решаемости данного задания на экзамене свидетельствовал о том, что большинство учеников изучили шаблон программного решения и успешно его применяли. Можно ли пример 13 задания обозначить как недостаток «шаблонных методов решения задач»? По нашему мнению, нет. Успешно решить задачу без понимания алгоритмической идеи и знания синтаксических средств языка было невозможно. Ученик должен понимать рекурсию — один из фундаментальных принципов программирования, уметь пользоваться условиями — базовый необходимый навык, знать и вариативно изменять генераторы списочных выражений, понимать принципы работы со словарями с строками. Однозначно положительными сторонами решения можно назвать его компактность, универсальность и вариативность, то есть незначительные изменения кода позволяли решать широкий спектр задач внутри конкретного типа. По нашему мнению, подобная ситуация ожидает в ближайшие годы целый ряд заданий в ЕГЭ по информатике, как то, задачи 1, 2,5,8,14, 15, 16. Это обусловлено компьютерной формой экзамена и возможности применения многочисленных авторских идей и алгоритмов, реализуемых в программном коде. Как только шаблон позволяет решать с незначительными изменениями весь спектр задач внутри типа, разработчики изменяют задание. Так произошло и с номером 13, когда ориентированный граф был заменён на ip-адреса. [4, с.23]
Однако, необходимо заметить, что история шаблона на этом не закончилась. Несмотря на квадратичную асимптотику, идея решения может выгодно применяться для решения задания 9 ОГЭ по информатике, задания 4 ОГЭ по информатике, задания 8 ЕГЭ по информатике. Подобная масштабная вариативность обусловлена, конечно же, рекурсивной природой алгоритма, а также удобным переводом таблиц в структуры данных через генератор словаря. Приведём примеры реализации данного алгоритма для задания 4. [3]

Рис. 6
В данном задании описываемый алгоритм может способствовать визуальному решению, иначе, получить количество возможных путей таблицы, и, уже потом, сопоставить расстояния между узлами рёбер графа.

Рис. 7.
Вместо sum() используем генератор.join() — для вывода строки, базовым случаем рекурсии будет вывод на экран итогового пути. Чтобы избежать повторов и цикличных путей, добавляем в генератор условие if c.count(x)<1. Таким образом, в 5 строчек кода мы получаем визуальную помощь в решении 4 задания, что особенно актуально для перепроверки ответа на экзамене или прототипа с большим количеством путей. Подобную идею рекурсии можно реализовать и в решении 8 задания ЕГЭ по информатике, причём, тем же шаблоном. Задание демоверсии 2025 года требует от нас определить количество двенадцатиричных пятизначных чисел, в записи которых ровно одна цифра 7 и не более трёх цифр с числовым значением, превышающим 8.

Рис. 8
Решение данного задания через рекурсию выглядит компактно. Перед базой рекурсии описываем случаи, когда функция будет выводить 0, генератор sum() подсчитывает количество вариантов, он же добавляет в строчку следующие символы. Необходимо отметить, что подобное решение выгодно отличает от классического решения на циклах большой запас по памяти. Возможность рекурсивного подсчёта и, если требуется, добавление мемоизации позволяет обрабатывать действительно большой объём данных.
В данной работе мы рассмотрели историю развития универсальной алгоритмической идеи, реализация в программном коде которой может быть, в полной мере, охарактеризована как «шаблон». В статье предпринята попытка рассмотреть «шаблонные решения» не в негативном, но позитивном смысле, подчёркивая, что универсальность идеи кода не может являться отрицательным маркером в вопросе его использования. Выпускник может познакомиться с идеей решения задач через рекурсию уже в 9 классе, при решении задач № 4,9, затем успешно применять данный алгоритм на ЕГЭ по информатике в заданиях 8, 16. Универсальные, шаблонные решения не есть негативный элемент в подготовке к экзамену, напротив, масштабность алгоритма, простота реализации позволяет знакомить учеников со сложными синтаксическими конструкциями языка программирования, экономить время на решении задания и успешно сдать экзамен в целом.
Литература:
- Кабанов, А. М. Разбор задания 13_5700 / А. М. Кабанов. — Текст: электронный // Вконтакте: [сайт]. — URL: https://vk.com/video-205865487_456239360 (дата обращения: 24.09.2024).
- Демоверсии, спецификации, кодификаторы. — Текст: электронный // Федеральный институт педагогических измерений: [сайт]. — URL: https://fipi.ru/ege/demoversii-specifikacii-kodifikatory (дата обращения: 24.09.2024).
- Демоверсии, спецификации, кодификаторы. — Текст: электронный // Федеральный институт педагогических измерений: [сайт]. — URL: https://fipi.ru/oge/demoversii-specifikacii-kodifikatory (дата обращения: 24.09.2024).
- Крылов, С. С. Аналитические и методические материалы / С. С. Крылов. — Текст: электронный // Федеральный институт педагогических измерений: [сайт]. — URL: https://doc.fipi.ru/ege/analiticheskie-i-metodicheskie-materialy/2023/inf_mr_2023.pdf (дата обращения: 24.09.2024).
Похожие статьи
Парадигматический аспект изучения семантики противоположности в начальной школе
Статья посвящена проблеме изучения семантики противоположности в парадигматическом аспекте на уроках русского языка и литературного чтения в начальной школе. Рассматриваются антонимы как один из типов лексико-семантической парадигмы и их функциониров...
О применении конкретной информационной технологии в обучении студентов математическому анализу
В статье рассказывается о применении информационных технологий, в частности QR-кодов, в высшем образовании, на примере дисциплины — математический анализ. Излагаются проблемы, которые встают перед преподавателем и студентом в настоящее время. Даётся ...
Геометрические задачи как основа обучения школьников выделению существенных признаков геометрических объектов
В статье рассматриваются вопросы обучения школьников выделению существенных признаков геометрических объектов на основе исследования как методики развития математического мышления у школьников в рамках личностно-ориентированного обучения. Выделены о...
Решение нестандартных задач по физике как фактор развития эвристического мышления обучающихся
В статье автор рассматривает проблему формирования творческого мышления обучающихся на занятиях по физике средствами решения нестандартных задач.
Метапредметная сущность логических знаний и умений в школьном курсе физики
В статье отражена метапредметная сущность логических знаний и умений в школьном курсе физики, рассмотрены элементы логики метапредметного содержания и приведены примеры заданий.
Методика решения олимпиадных задач по информатике в школе
В статье представлены как общие методические подходы к обучению решению олимпиадных задач по информатике, так и методика обучения решению задач. В качестве решения олимпиадных задач предлагается результат применения цифровой образовательной среды. Та...
Практико-ориентированные задачи как средство формирования функциональной грамотности при обучении математике
Данная статья посвящена роли практико-ориентированных задач в обучении математике и их значимости при формировании у учащихся функциональной грамотности.
Методы и приемы введения математических понятий в начальном курсе математики
В статье автор анализирует виды определения математических понятий, методы и приемы их осознанного усвоения младшими школьниками (на примере УМК «Школа России»).
Системно-деятельностный подход при изучении алгоритмизации и программирования учащимися в основной школе
Сфера современного образования нуждается в глобальных перестройках. Данная задача актуализируется ввиду развития современного технологического прогресса и необходимости обеспечения активной и разносторонней организации обучения. Основной целью текуще...
Метод проектов в обучении элементам теории графов
В данной статье был рассмотрен метод проектов, позволяющий построить обучение на активной деятельности ученика. Подробно описаны проект на тему «Графы вокруг нас» и организация работы над ним. Этот проект можно предложить учащимся 5-6 классов в рамка...
Похожие статьи
Парадигматический аспект изучения семантики противоположности в начальной школе
Статья посвящена проблеме изучения семантики противоположности в парадигматическом аспекте на уроках русского языка и литературного чтения в начальной школе. Рассматриваются антонимы как один из типов лексико-семантической парадигмы и их функциониров...
О применении конкретной информационной технологии в обучении студентов математическому анализу
В статье рассказывается о применении информационных технологий, в частности QR-кодов, в высшем образовании, на примере дисциплины — математический анализ. Излагаются проблемы, которые встают перед преподавателем и студентом в настоящее время. Даётся ...
Геометрические задачи как основа обучения школьников выделению существенных признаков геометрических объектов
В статье рассматриваются вопросы обучения школьников выделению существенных признаков геометрических объектов на основе исследования как методики развития математического мышления у школьников в рамках личностно-ориентированного обучения. Выделены о...
Решение нестандартных задач по физике как фактор развития эвристического мышления обучающихся
В статье автор рассматривает проблему формирования творческого мышления обучающихся на занятиях по физике средствами решения нестандартных задач.
Метапредметная сущность логических знаний и умений в школьном курсе физики
В статье отражена метапредметная сущность логических знаний и умений в школьном курсе физики, рассмотрены элементы логики метапредметного содержания и приведены примеры заданий.
Методика решения олимпиадных задач по информатике в школе
В статье представлены как общие методические подходы к обучению решению олимпиадных задач по информатике, так и методика обучения решению задач. В качестве решения олимпиадных задач предлагается результат применения цифровой образовательной среды. Та...
Практико-ориентированные задачи как средство формирования функциональной грамотности при обучении математике
Данная статья посвящена роли практико-ориентированных задач в обучении математике и их значимости при формировании у учащихся функциональной грамотности.
Методы и приемы введения математических понятий в начальном курсе математики
В статье автор анализирует виды определения математических понятий, методы и приемы их осознанного усвоения младшими школьниками (на примере УМК «Школа России»).
Системно-деятельностный подход при изучении алгоритмизации и программирования учащимися в основной школе
Сфера современного образования нуждается в глобальных перестройках. Данная задача актуализируется ввиду развития современного технологического прогресса и необходимости обеспечения активной и разносторонней организации обучения. Основной целью текуще...
Метод проектов в обучении элементам теории графов
В данной статье был рассмотрен метод проектов, позволяющий построить обучение на активной деятельности ученика. Подробно описаны проект на тему «Графы вокруг нас» и организация работы над ним. Этот проект можно предложить учащимся 5-6 классов в рамка...







