Расчет несимметричных трехфазных цепей
Автор: Соловьев Владимир Алексеевич
Рубрика: Электротехника
Опубликовано в Техника. Технологии. Инженерия №1 (3) январь 2017 г.
Дата публикации: 02.01.2017
Статья просмотрена: 6807 раз
Библиографическое описание:
Соловьев, В. А. Расчет несимметричных трехфазных цепей / В. А. Соловьев. — Текст : непосредственный // Техника. Технологии. Инженерия. — 2017. — № 1 (3). — С. 17-22. — URL: https://moluch.ru/th/8/archive/46/1861/ (дата обращения: 24.04.2025).
Трехфазные системы передачи электрической энергии состоят из источников энергии, линий передачи, трансформаторов и электродвигателей. В результате какой-либо аварии (например, короткого замыкания или обрыва провода) или при несимметричной нагрузке на элементах системы (электродвигателях, трансформаторах, самой линии передачи) возникают несимметричные напряжения.
Распространенным случаем аварии в трехфазной системе является короткое замыкание на землю. Короткие замыкания, как правило, сопровождаются увеличением токов в поврежденных фазах до значений, превосходящих в несколько раз номинальные значения, а также понижением уровня напряжения в электрической сети.
Протекание токов КЗ приводит к увеличению потерь электроэнергии в проводниках и контактах, что вызывает их повышенный нагрев. Нагрев может ускорить старение и разрушение изоляции, вызвать сваривание и выгорание контактов, потерю механической прочности шин и проводов и т. п.
Снижение напряжения на шинах у потребителя может привести к опасным последствиям. Особенно чувствительна к снижениям напряжения двигательная нагрузка. При глубоких снижениях напряжения уменьшается вращающий момент электродвигателя до значений, меньших момента сопротивления механизма. Электродвигатель тормозится, что влечет за собой увеличение потребляемого им тока. При этом еще больше увеличивается падение напряжения в сети, вследствие чего может развиться лавинообразный процесс, захватывающий все большее количество потребителей электроэнергии [4].
Обобщая вышесказанное, можно сделать вывод, что расчет токов короткого замыкания является одной из главных задач энергетики. Необходимость определения токов КЗ в процессе эксплуатации может возникнуть:
‒ при изменении схемы питания энергетического объекта для проверки электрооборудования на термическое и электродинамическое действие токов КЗ, пригодности существующих установок релейной защиты, средств грозозащиты;
‒ при частичной замене электрооборудования на электростанции или подстанции, если намеченные к установке машины и аппараты по своим паспортным данным отличаются от демонтируемых;
‒ вследствие изменения условий эксплуатации электрического объекта;
‒ при создании нового энергетического объекта [3, c. 3].
Целью работы является рассмотрение метода симметричных составляющих и его практическое применение для расчета токов короткого замыкания.
Основным методом расчета несимметричных трехфазных систем является метод симметричных составляющих. Для описания основных положений метода симметричных составляющих, проведем расчет простой трехфазной цепи с несимметричным источником.
Параметры элементов: EA = 100∙![]() В; EB = 150∙
В; EB = 150∙![]() В; EC = 120∙
В; EC = 120∙![]() В; L = 6 мГн; R = 5 Ом. Найти токи: IA, IB, IC.
В; L = 6 мГн; R = 5 Ом. Найти токи: IA, IB, IC.
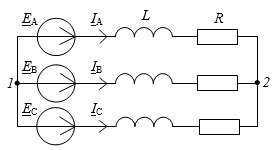
![]() Рис. 1. Исходная схема цепи
Рис. 1. Исходная схема цепи
Расчет токов методом симметричных составляющих. Раскладываем напряжения и токи, на напряжения и токи прямой, обратной и нулевой последовательности [1, с. 200]
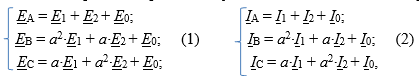
где a = ![]() - оператор трехфазной системы; индексом 1 обозначается прямая последовательность; индексом 2 обозначается обратная последовательность; индексом 0 обозначается нулевая последовательность.
- оператор трехфазной системы; индексом 1 обозначается прямая последовательность; индексом 2 обозначается обратная последовательность; индексом 0 обозначается нулевая последовательность.
Cоставим для схемы на рис.1 уравнение по первому закону Кирхгофа:
IA + IB + IC = 0; (3)
Решая системы (1) и (2), найдем E1, E2, E0 и I1, I2, I0;
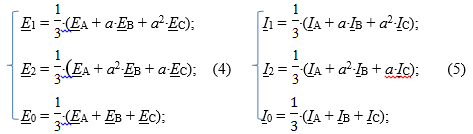
При подстановке уравнения (3) в систему (5) ток нулевой последовательности будет равен нулю. Следовательно, напряжения и токи цепи не будут содержать составляющую нулевой последовательности [2, с. 26].
Рассчитаем эквивалентное сопротивление:
ZЭ = j![]() L + R = j 1,9 +5 = 5,3∙
L + R = j 1,9 +5 = 5,3∙![]() Ом.
Ом.
Составим эквивалентные схемы замещения цепи для прямой и обратной последовательности рис.2.
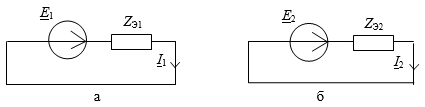
Рис. 2. Схема замещения цепи для прямой (а) и обратной (б) последовательности
Нагрузка симметрична поэтому эквивалентные сопротивления прямой и обратной последовательности равны: ZЭ = ZЭ1 = ZЭ2.
Находим токи прямой и обратной последовательности по закону Ома:
![]()
![]() I1 =
I1 = ![]() ; I2 =
; I2 = ![]() .
.
Подставим численные значения и найдем E1, E2:
E1 =![]() ∙(100∙
∙(100∙![]() +
+ ![]() ∙150∙
∙150∙![]() +
+ ![]() ∙120∙
∙120∙![]() ) = 120,3∙
) = 120,3∙![]() В;
В;
E2 =
Для проверки правильности нахождения E1, E2 построим векторную диаграмму.
Используя метод сложения векторов, по формулам системы (4) строим векторы E1, E2. Векторная диаграмма приведена на рис.3.
![]()
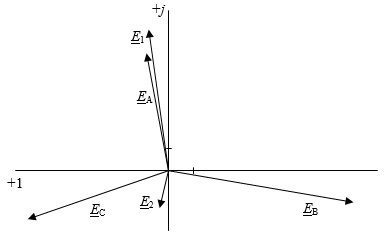
Рис.3. Векторная диаграмма источников ЭДС
Подставляем найденные значения в систему (2):
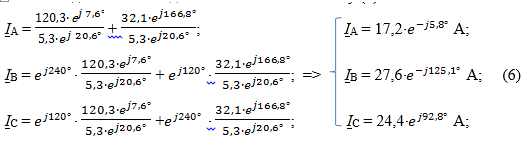
Расчет тока короткого замыкания линейного провода на землю. Исходная схема приведена на рис.4. Требуется аналитически провести расчет тока короткого замыкания линейного провода на землю.
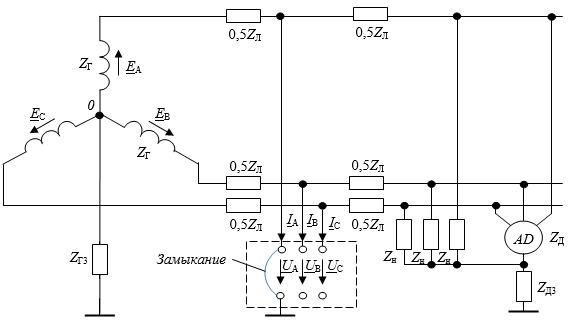
Рис.4. Исходная схема цепи
Составим эквивалентные схемы замещения цепи для прямой, обратной и нулевой последовательности рис.5.
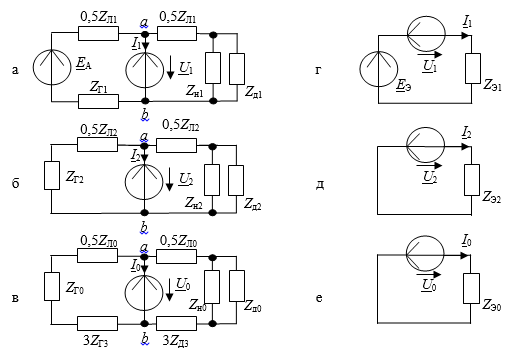
Рис. 5. Схемы замещения для прямой, обратной и нулевой последовательности
Место аварии на рис.4 окружено штриховой линией. Несимметричные напряжения, образовавшиеся в месте аварии, обозначены UA, UB, UC, а токи на землю в месте аварии IA, IB, IC. Из рисунка видно, что UA = 0, и IB = IC = 0. В соответствии с методом симметричных составляющих три фазных напряжения и три фазных тока представим через их симметричные составляющие:

где a = ![]() — оператор трехфазной системы; индексом 1 обозначается прямая последовательность; индексом 2 обозначается обратная последовательность; индексом 0 обозначается нулевая последовательность.
— оператор трехфазной системы; индексом 1 обозначается прямая последовательность; индексом 2 обозначается обратная последовательность; индексом 0 обозначается нулевая последовательность.
Схема на рис.5, а составлена для токов и напряжений прямой последовательности в фазе А, схема на рис.5, б составлена для токов и напряжений обратной последовательности в фазе В, схема на рис.5, в составлена для токов и напряжений нулевой последовательности в фазе С, Так как генератор дает симметричную систему ЭДС прямой последовательности EA, EB, EC, а ЭДС обратной и нулевой последовательностей не содержит, то ЭДС EA имеется только в схеме на рис.5,а, в схемах на рис.5,б,в ЭДС генератора отсутствует.
Утроение сопротивления заземления генератора и двигателя в схеме на рис.5,е для нулевой последовательности объясняется тем, что по нулевому проводу течет ток, в три раза больший, чем по фазовому проводу [1, c. 205].
Схемы на рис.5, а, б, в, заменяем их эквивалентами на рис.5, г, д, е, не затрагивая при этом источники ЭДС, напряжение на которых равно U1, U2, U0.
Параметры схемы на рис. 5, г (находим EЭ методом эквивалентного генератора):
zэ1 = 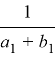 ; EЭ =
; EЭ = 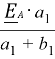 ;
;
a1 = 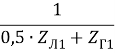 ; b1 =
; b1 = 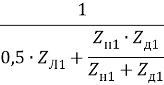 .
.
Параметры схемы на рис. 5, д:
zэ2 = 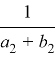 ; a2 =
; a2 = 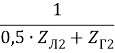 ; b2 =
; b2 = 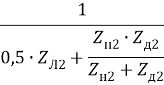 .
.
Параметры схемы на рис. 5, e:
zэ0 = 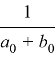 ; a0 =
; a0 = 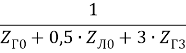 ; b0 =
; b0 = 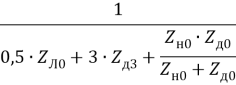 .
.
Затем для схем на рис5, г, д, е составляем уравнения по второму закону Кирхгофа:
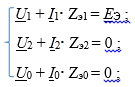 (9)
(9)
Исходя из исходных данных UA = 0, и IB = IC = 0, мы можем найти ток на фазе А, который равен току короткого замыкания. Решаем систему (9) путем сложения всех её уравнений:
U1 + U2 + U0 + (I1 + I2 + I0)![]() (Zэ1+ Zэ2 + Zэ0) = EЭ. (10)
(Zэ1+ Zэ2 + Zэ0) = EЭ. (10)
Согласно уравнениям систем (7) и (8), заменяем сумму симметричных составляющих напряжений и токов на UA, IA. Уравнение (10) примет вид:
IA![]() (Zэ1+ Zэ2 + Zэ0) = EЭ;
(Zэ1+ Zэ2 + Zэ0) = EЭ;
IКЗ = IA= 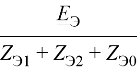 .
.
Вывод. Расчет несимметричных трехфазных цепей является важным вопросом в энергетике, так как правильность его расчета влияет не только на энергоэффективность, но и на безопасность рабочих. Метод симметричных составляющих хорошо справляется с этой задачей, так как данный метод позволяет перейти от несимметричной системы, к симметричной, ведь тогда оказывается возможным исключить соотношения, обусловленные взаимоиндукцией, и избежать связанных с ними осложнений при решении тех или иных вопросов.
Литература:
- Бессонов Л. А. Теоретические основы электротехники. Электрические цепи: учебник для бакалавров / Л. А. Бессонов. — 12-е изд., исправ. и доп. — М.: Издательство Юрайт, 2014. — 701 с.
- Вагнер К. Ф., Эванс Р. Д. Метод симметричных составляющих. / К. Ф. Вагнер, Р. Д. Эванс. Л — М.: ОНТИ, 1936. — 407 с.
- Беляева Е. Н. Как рассчитать ток короткого замыкания. — 2-е изд. перераб. и доп. — М.: Энергоатомиздат, 1983. — 136 с.
- Короткие замыкания в электроустановках // Все об электростанциях. URL: http://www.gigavat.com/obschie_svedeniya_ob_elektroustanovkah5.php (дата обращения: 28.12.2016).







