Методы интеллектуального анализа данных в диагностировании сердечно-сосудистых заболеваний
Авторы: Розыходжаева Дилдора Аброровна, Розыходжаева Гульнора Ахмедовна
Рубрика: Общие вопросы технических наук
Опубликовано в Техника. Технологии. Инженерия №3 (5) июнь 2017 г.
Дата публикации: 04.06.2017
Статья просмотрена: 1217 раз
Библиографическое описание:
Розыходжаева, Д. А. Методы интеллектуального анализа данных в диагностировании сердечно-сосудистых заболеваний / Д. А. Розыходжаева, Г. А. Розыходжаева. — Текст : непосредственный // Техника. Технологии. Инженерия. — 2017. — № 3 (5). — С. 4-8. — URL: https://moluch.ru/th/8/archive/62/2542/ (дата обращения: 03.04.2025).
На сегодняшний день проблема высокой смертности населения ввиду сердечно-сосудистых заболеваний остается одной из самых критичных проблем здравоохранения. Люди, страдающие заболеваниями сердца или подвергающиеся высокому риску их возникновения, нуждаются в раннем выявлении и оказании помощи путем консультирования и, при необходимости, приема лекарственных средств и госпитализации.
Благодаря стремительному развитию информационно-коммуникационных технологий, способствующих быстрому накоплению, обработке и передаче на расстояние больших объемов цифровой информации, появилась возможность производить анализ огромных массивов данных и, используя их в качестве обучающей выборки, строить сложные математические модели для принятия врачебных решений. Для реализации подобных задач создаются специализированные информационные системы поддержки принятия решений, основное предназначение которых состоит в формализации слабоструктурированных и неструктурированных задач планирования, прогнозирования и управления [1].
Интеллектуальный анализ данных в медицине, применяемый для построения медицинских диагностических систем, предназначен для того, чтобы помочь врачу, в частности, малоопытному специалисту, свести к минимуму диагностические ошибки и ускорить процесс принятия решения для повышения качества медицинского обслуживания. Различные алгоритмы, связанные с интеллектуальным анализом данных, значительно помогают понять медицинские данные более четко путем выделения патологических данных из нормальных данных, поддержки принятия решений, а также визуализации и идентификации скрытых сложных взаимосвязей между диагностическими особенностями разных групп пациентов. [2]
Индуктивные методы обучения, такие как наивный байесовский классификатор, имеют большой успех в построении классификационных моделей с целью минимизации ошибок классификации. В качестве модификации алгоритма многие предыдущие исследования индуктивного обучения также рассматривали способы сведения к минимуму затрат на ошибки классификации, такие как стоимость ложных срабатываний и стоимость ложного отрицания в задачах бинарной классификации. [3]
Издержки неправильной классификацией полезны при принятии решения о том, склонна ли разработанная модель принимать правильные решения о присвоении меток класса для новых данных, но это не единственные издержки, которые необходимо учитывать на практике. При проведении классификации по новому примеру мы часто рассматриваем «затраты на испытания», когда недостающие значения должны быть получены с помощью физических «тестов», которые сами по себе несут расходы. Эти затраты часто также важны, как и ошибки в классификации.
В качестве примера рассмотрим задачу медицинской практики, которая исследует приходящих пациентов c определенными заболеваниями. Предположим, что предыдущий опыт врачей был скомпилирован в классификационную модель, такую как наивный байесовский классификатор. При диагностировании нового пациента часто бывает, что определенная информация для этого патента может еще не быть известна; Например, анализ крови или рентгеновский анализ, возможно, еще не были проведены. Выполнение этих тестов повлечет за собой определенные дополнительные расходы, но различные тесты могут обеспечить различные информационные ценности для минимизации затрат на неправильную классификацию. Именно балансирование двух видов расходов — а именно, затрат на неправильную классификацию и затрат на испытания — определяет, какие тесты будут выполняться.
Задачи, которые влекут за собой как неправильную классификацию, так и затраты на исследования, изобилуют в практике: от постановки медицинского диагноза до научного исследования и разработки новых лекарственных средств. Одним из возможных подходов решения проблемы является использование стратегии наивной классификации Байеса при рассмотрении недостающих значений. То есть, когда тестовый случай классифицируется наивным классификатором Байеса, и обнаруживается, что у атрибута есть пропущенное значение, тест не будет выполнен для получения его значения; Вместо этого атрибут просто игнорируется в данном вычислении. Задача с этим подходом заключается в том, что она игнорирует возможность получения отсутствующего значения со стоимостью и, таким образом, уменьшает стоимость ошибки классификации и общую стоимость исследования.
Байесовский классификатор представляет собой широкий класс алгоритмов классификации, основанный на принципе максимума апостериорной вероятности. Для классифицируемого объекта вычисляются функции правдоподобия каждого из классов, по ним вычисляются апостериорные вероятности классов. Объект относится к тому классу, для которого апостериорная вероятность максимальна. Алгоритм предполагает, что наличие какого-либо одного признака в классе не связано с наличием какого-либо другого признака.
Упрощенно формулу для данного алгоритма можно представить следующим образом
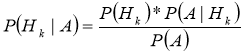 , (1)
, (1)
где P(Hk) — априорная вероятность события Hk
P(Hk|A) — вероятность события Hk при наступлении А
P(A| Hk) — вероятность события A при наступлении Hk
P(A) — полная вероятность события А
В качестве примера можно рассмотреть работы таких ученых как Роберт С. Ледли и Ли Б. Ластид, в которой излагается использование формулы Байеса для оценки вероятности постановки диагноза на основе предположения о том, что данные/симптомы для конкретного заболевания не являются взаимозависимыми. Например, вероятность того, что у пациента с симптомами кашля и лихорадки есть диагноз пневмония, вычисляется как:
![]() ,(2)
,(2)
где P (cough | pnuemonia) указывает на вероятность кашля с учетом диагноза пневмонии. Предположение, сделанное для упрощения, состоит в том, что зависимость между лихорадкой и кашлем отсутствует. [4]
Одним из самых ранних исследований подхода Наивного Байеса занимался Гомер Уорнер из Университета штата Юта. Уорнер создал вероятностную модель для диагностики пациентов с одним из 35 врожденных пороков сердца. [5] Модель исследовала частоту вхождения каждого из 50 различных признаков при выявлении каждого заболевания и распространённость заболевания в популяции пациентов, направляемых в его лабораторию. Исследование Уорнера привело к разработке информационной системы HELP [6], которая стала первой информационной системой в больницах с модулями поддержки принятия решений. На протяжении многих лет функции поддержки принятия решений расширялись, чтобы предоставлять предупреждения, напоминания, интерпретацию данных, диагностику пациентов, рекомендации по управлению пациентами и клинические протоколы.
Другие ранние применения байесовского подхода включают диагностику гематологических нарушений и аппендицита. Более поздние разработки применялись для лечения боли в животе, одонтогенных повреждений, онкологии, заболеваний печени, панкреатита, болезни легких, стоматологии, гинекологии, неврологии, ревматологии, дерматопатологии, офтальмологии, гематопатологии, гипертонии, сердечных заболеваний, побочных реакций и патологии кишечника. Многие приложения, основанные на наивном байесовском классификаторе, достигли производительности, которая была сопоставима с человеческими врачами, и некоторые из них были успешно развернуты в медицинских учреждениях.
Преимущество модели Байеса заключается в том, что она позволяет осуществить классификации в случаях отсутствия части входных признаков, в отличие от других широко применяемых на сегодняшний день математических моделей. Такое свойство позволяет ускорить процесс принятия решений в кардиологии, основываясь только на имеющихся в момент проведения исследования данных.
Для исследования модели принятия решений при диагностике диастолической дисфункции левого желудочка (ДДЛЖ) на основе корреляционного анализа данных были выявлены 26 входных признаков, наиболее ярко влияющих на выявление данной патологии. Для каждого выявленного нарушения параметра на основе обучающей выборки рассчитан вектор частоты вхождения признака в случае обнаружения и отсутствия ДДЛЖ (Таблица 1). Предварительно обучающая выборка была подвергнута процессу нормализации путем замены числовых признаков на показатель выявления/не выявления нарушения.
Таблица 1
Частота вхождения параметра при выявленной иотсутствующей патологии
|
№ |
Наименование признака |
При выявленном ДДЛЖ |
При отсутствии ДДЛЖ |
|
1 |
Каротидная эндартерэктомия |
0,67052 |
0,081395 |
|
2 |
Хроническая сердечная недостаточность |
0,36416 |
0,75 |
|
3 |
Наличие нарушения согласно NYHA |
0,30636 |
0,69186 |
|
4 |
Сахарный диабет |
0,50867 |
0,25 |
|
5 |
Курение |
0,22543 |
0,05814 |
|
6 |
Положительный семейный анамнез |
0,13873 |
0,023256 |
|
7 |
Наличие инсульта |
0,49711 |
0,22093 |
|
8 |
Дисциркуляторная энцефалопатия |
0,24855 |
0,69186 |
|
9 |
Остеохондроз |
0,24855 |
0,656977 |
|
10 |
Заболевания желудочно-кишечного тракта |
0,30058 |
0,860465 |
|
11 |
Ингибиторы АПФ, блокаторы ангиотензиновых рецепторов |
0,84971 |
0,604651 |
|
12 |
Прием статинов |
0,6185 |
0,343023 |
|
13 |
Прием аспирина |
0,88439 |
0,715116 |
|
14 |
Наличие нарушения общего холестерина крови |
0,0289 |
0,261628 |
|
15 |
Наличие нарушения липопротеидов низкой плотности |
0,0289 |
0,145349 |
|
16 |
Наличие нарушения индекса атерогенности |
0,7052 |
0,889535 |
|
17 |
Наличие нарушения коэффициента атерогенности |
0,84393 |
0,918605 |
|
18 |
Наличие нарушения степени каротидного стеноза |
0,9711 |
0,837209 |
|
19 |
Наличие опасного тип атеросклеротической бляшки |
0,91329 |
0,889535 |
|
20 |
Наличие нарушения конечно-диастолического объема левого желудочка |
0,23699 |
0,47093 |
|
21 |
Наличие нарушения диаметра левого предсердия |
0,3526 |
0,25 |
|
22 |
Наличие нарушения конечно-систолического размера левого желудочка |
0,54913 |
0,168605 |
|
23 |
Наличие нарушения конечно-систолического объема левого желудочка |
0,76879 |
0,511628 |
|
24 |
Наличие нарушения толщины межжелудочковой перегородки |
0,83237 |
0,244186 |
|
25 |
Наличие нарушения ударного объема сердца |
0,4104 |
0,319767 |
|
26 |
Наличие нарушения толщины задней стенки левого желудочка |
0,97688 |
0,645349 |
|
Общая частота выявления ДДЛЖ |
0,50145 |
||
С помощью полученной итоговой матрицы проведен ряд экспериментов по выявлению ДДЛЖ на основе различного набора входных параметров. Эксперимент заключался в вычислении показателей вероятности выявления ДДЛЖ и его отсутствия. При этом в классификации выигрывал тот показатель, значения которого было больше.
Так, для набора параметров x2, x3, x7, x8, x9, x10, x13, x16, x17, x26 показатель вероятности наличия ДДЛЖ составил 0,00026553, а показатель отсутствия — 0,00842964, следовательно, модель в качестве ответа сообщит пользователю об отсутствия исследуемой патологии у больного, что, в действительности, является верным ответом. В случае, кода в качестве входных параметров наблюдались x1, x7, x11, x12, x13, x18, x19, x26 модель выдала показатели, равные 0,0673070 и 0,0006391 для наличия и отсутствия заболевания соответственно, следовательно, система выдает заключение об обнаружении у пациента отклонения.
Увеличение количества входных параметров также не оказало влияние на точность работы системы. Так, на экспериментальном примере из 18 входных параметров, которые включали x2, x5, x7, x8, x9, x10, x11, x12, x13, x16, x17, x18, x19, x20, x21, x23, x25, x26, система сумела верно диагностировать ДДЛЖ с результатами показателей вероятности 0,0000024 против 0,0000021.
Таким образом, Байесовский классификатор достаточно адекватно определяет нарушения, присваивая им относительно высокую априорную вероятность в отдельных клинических случаях. Модель проста в реализации и имеет низкие вычислительные затраты при обучении и классификации. Однако, следует отметить, что в случаях, когда значения параметров вероятности достаточно близки друг к другу, стоит запросить ввод дополнительных данных, либо оставить право принятия решения за медицинским работником.
Литература:
- Халафян А. А. Анализ и синтез медицинских систем поддержки принятия решений на основе технологий статистического моделирования: автореф. дис.... д-р. тех. наук: 05.13.01. Краснодар, 2010.
- U. Rajendra Acharya, Wenwei Yu Data Mining Techniques in Medical Informatics // The Open Medical Informatics Journal. — 2010. — № 4, p. 21–22
- Xiaoyong Chai, Lin Deng, Qiang Yang, Charles X. Ling Test-Cost Sensitive Naive Bayes Classification // Proceedings of the Fourth IEEE International Conference on Data Mining. — 2004. — № ICDM '04, p. 51–58.
- Robert S. Ledley and Lee B. Lusted. Reasoning foundations of medical diagnosis; symbolic logic, probability, and value theory aid our understanding of how physicians reason. Science, 130(3366):9–21, 1959.
- H. R. Warner, A. F. Toronto, L. G. Veasey, and R. Stephenson. A mathematical approach to medical diagnosis. application to congenital heart disease. JAMA: the journal of the American Medical Association, 177:177–183, July 1961.
- R. S. Evans. The help system: a review of clinical applications in infectious diseases and antibiotic use. M.D. computing: computers in medical practice, 8(5), 1991.







