Бир ва кўп ўлчовли полинимиал сплайнлар ёрдамида ҳисоблаш усуллари
Авторы: Худайберганов Тимур Рустамович, Искандаров Санжар Кувондикович
Рубрика: Спецвыпуск
Опубликовано в Техника. Технологии. Инженерия №3 (5) июнь 2017 г.
Дата публикации: 14.07.2017
Статья просмотрена: 103 раза
Библиографическое описание:
Худайберганов, Т. Р. Бир ва кўп ўлчовли полинимиал сплайнлар ёрдамида ҳисоблаш усуллари / Т. Р. Худайберганов, С. К. Искандаров. — Текст : непосредственный // Техника. Технологии. Инженерия. — 2017. — № 3 (5). — С. Т.1. 43-46. — URL: https://moluch.ru/th/8/archive/62/2589/ (дата обращения: 26.04.2025).
Кириш
Сплайнларни экспериментал маълумотлар асосида қуриш (аналитик ва жадвалда берлиганларига кўра) би коэффициентларини топишдан иборат бўлади. Умумий ҳолларда эса Δ – сплайн тўрини аниқлашдан иборат бўлади.
Калит сўзлар: сплайн, интерполяцион, экспериментал, cплайн тўри
Коэффициентларни аниқлашнинг турли усуллари мавжуд. Интерполяцион ва локал формулалар, силлиқловчи сплайнлар, локал сиқиш, энг кичик квадратларнинг интерполяцион методи шулар жумласидандир. [1,2,3]
Интерполяцион сплайн қуришда тўрлар Δ тўрлардан қўшимча х-1, х-2, х и+1, +2 тугунларини қўшиш орқали юзага келади. би коэффициентларини аниқлаш учун чизиқли тенгламаларнинг системасига эга бўламиз:
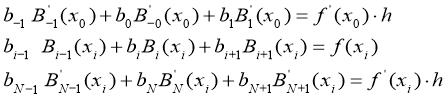
Бу ерда ҳ= х и+1 – хи – интерполяциянинг қадами.
ф '(х0) ва ф '(хН) – тўрлар якунидаги функциялар ҳосиласи.
Бу системанинг матрицаси уч диагоналлидир. Биринчи ва охирги тенглама эса унга келтирилади. Қуйидаги схема хатоликни кўрсатади:
Ҳисоблаш муаммолари локал сплайн-аппроксимацияга мурожаат қилинганда сезиларли равишда соддалашади. Уларда яқинлашувчи сплайн функциянинг қиймати ҳар бир кесмада фақат ушбу кесманинг баъзи қисмларидан олинган апрроксимацияланаётган функциянинг қийматига боғлиқ бўлади. Бундай методларнинг яна бир хусусияти шундаки, сплайннинг параметрларини топишда алгебраик тенглама системасини ечишни талаб қилмайди. Ҳисоблаш ишларининг зарурий ҳажми Δ тўрлари тугунининг миқдорига боғлиқ эмас, балки сплайннинг даражаси билан аниқланади. Шунинг учун у интерполяцион сплайнни қуришдагига нисбатан анчайин кичкинадир. Ҳосил бўладиган яқинлашиш формулалари эса аниқлик жиҳатидан қолишмайди.
Ишларда [3] коэффициентларни би = б(ф(х)) формулалари асосида ҳисоблаш йўли билан олиш мумкинлиги кўрсатилган. Ҳисоблаш операцияларининг ҳажми ва параллеллаштириш ҳамда конвейерлаштириш жараёнлари ташкиллаштириш имкониятларини баҳолаш учун бу формулаларни тайёр ҳолда келтириш мақсадга мувофиқдир. Қуйида келтирилган формулаларни К-нуқтали, деб атаймиз. Иккинчи даражали сплайнлар учун:
1) уч нуқтали
![]()
2) 5 нуқтали формула:
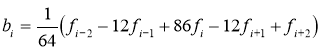
Локал формулалар яқинлашишнинг силлиқланиш хусусиятларини сақлаб қолади. Параметр қийматлари эса и индекси билан жорий нуқтадан етарли даражада узоқлашган нуқталардаги ҳисобга боғлиқ эмас. Улар симметрик бўлади. Лекин фақатгина соҳанинг ички нуқталари учун ишлайди.
Бундай ёндашувда чекка ҳудулардаги коэффициентларни аниқлаш борасида мураккабликлар вужудга келади. Уни аниқлаш учун қуйидаги усуллар таклиф этилган:
1. Чекка ҳудудлардаги коэффициентларни мавжуд формулалар асосида ҳисоблаш. Аммо бу, чекка ҳудудлардаги аппроксимация аниқлигининг пасайишига олиб келади.
2. Экспериментал маълумотларнинг бир қатор нуқталаридан сигнални аниқлаш чегарасидан ташқарида фойдаланиш. (агар бунинг имкони бўлса).
3. Чекка ҳудудларда сплайнларни эмас, балки 2-даражали Ньютон кўпҳадларини қўллаш.
Агарда экспериментал натижалар хатоликлар билан маълум бўлса, у ҳолда интерполяцион сплайн қуришнинг фойдаси йўқ. Бундай ҳолларда хатоликни камайтириш мақсадида силлиқловчи сплайнларни қўллаш зарурати юзага келади.
Силлиқловчи сплайн бу, интерполяциялангандан кўра «силлиқроқ» бўлган ва экспериментал қийматларга яқин жойдан ўтувчи сплайндир.
Функционални минималлаштирамиз:
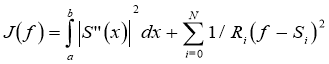 ,
,
Бу ерда Ри >0 берилган катталик. Ри нинг коэффициенти қанчалик кичик бўлса, сплайн-функция берилган қиймат фи га нисбатан шунчалик яқин ўтади.
Функционал юқоридаги функцияни минималлаштириш учун 5 диагонал матрицали чизиқли тенгламани ечиш зарур. Қурилган сплайн бўйича ортиқча кўпайтувчилар қайта ҳисобланади ва янги Ри асосида янги сплайн қурилади. Итерация жараёни сплайннинг қиймати берилган «коридор»га тўғри келгунича давом этиши керак. Мазкур методнинг камчилиги эксперимент натижаларини сиқишнинг истисно қилиниши бўлиб ҳисобланади.
Сигналларни бир вақтнинг ўзида сиқиш ва қайта тиклаш масалаларини ечишда энг кичик квадратлар методи яхши самара беради.
Яқинлашиш учун энг кичик квадратлар методи ишлатилган ҳолда функцияларнинг тугуни сплайнларнинг тугунига қараганда янада кўпроқ жойлашади.
Шу билан бирга функционални минималлаштириш керак:
 ,
,
Бу ерда С и – сплайн функция, фи – берилган функционал боғланиш.
1- жадвал. й = лн(х+1) функцияни локал формулалар ишлатган ҳолда аппроксимациялаш натижалари.
1- жадвал
|
Х |
ф(х) |
С(х) |
1% |
2% |
|
|
3-точеч. |
5-точеч. |
||||
|
2.5 |
1.252 |
1.245 |
1.250 |
0.430 |
0.124 |
|
2.75 |
1.321 |
1.311 |
1.318 |
0.621 |
0.187 |
|
3 |
1.386 |
1.375 |
1.382 |
0.683 |
0.248 |
|
3.25 |
1.447 |
1.436 |
1.443 |
0.683 |
0.248 |
|
3.5 |
1.500 |
1.495 |
1.500 |
0.31 |
0.000 |
|
3.76 |
1.560 |
1.556 |
1.561 |
0.248 |
0.062 |
|
4 |
1.610 |
1.601 |
1.605 |
0.559 |
0.310 |
Функционал  ни минималлаштириш учун чизиқли тенгламалар системасини ечиш зарур:
ни минималлаштириш учун чизиқли тенгламалар системасини ечиш зарур:
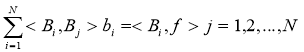
В-сплайнларнинг финитлиги туфайли тенгламалар системаси лентали матрицага эга. 2-даражали В-сплайнлар қўлланилганида системанинг матрицаси 5 диагоналли бўлади.
Сплайн тўри бир текис ҳолатда бўлганида тугунларнинг зарур миқдори масаласи кўндаланг қўйилади. Буни ҳал қилиш учун Хайес томонидан таклиф қилинган шовқин тестини қўллаш мумкин:
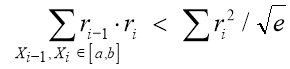
Бу ерда ри=фи – С и и =1,2,…, э
Шундай қилиб ишлов бериш талабларига боғлиқ ҳолда берилган хатоликда максимал сиқишга эришишимиз мумкин ёки экспериментал натижага янада яқинлашадиган функцияни излашимиз мумкин.
Хулоса
Шундай қилиб параболик сплайнлар билан яқинлашиш коэффициентларини ҳисоблаш методларини таҳлил қилиш шуни кўрсатдики, сплайн функцияларнинг тажриба натижалари асосида қуриш муамоси б – коэффициентларни ҳисоблаш масаласига олиб келади. Вақтнинг реал миқёсида ишловчи ситемалар учун коэффициентларни «нуқтали» ҳисоблаш формулалари таклиф этилади. В-сплайн эса жадвалли функция сифатида пайдо бўлиши мумкин. Боз устига полиномиал, тригонометрик, экспоненциал ва бошқа қаторлардан фарқли ўлароқ у ягона базис функция бўлади. Функцияларнинг базис сплайнлар тариқасида ифодаланиши ҳисоблаш структураси жадвал-алгоритмик метод қўлланилишини тақозо этадиган аппаратларда амалга оширилиши учун қулай ҳисобланади
Адабиётлар:
- Алексеев А.А., Агевич С.Н., Желедев В.А., Применение локальных сплайнов для цифровой обработки частотно-временных функций плотности распределения сигнальной энергии.//Радиотехника и радиоэлектроника. 2000, № 3, С.296-311.
- Зайнидинов Х.Н. Многопроцессорная вычислительная структура для восстановления многомерных сигналов на основе двумерных базисных сплайнов. В сб. научн. трудов VII-республиканской научн.-практич. конф. «Передовые технологии и методы в создании и эксплуатации авиакосмической техники», 21-23 апреля, Ташкент, 2004, С.20-22.
- Н.В. Момот Моделирование высокопроизводительных вычислительных структур на основе базисных сплайнов. // Тезисы докладов научно-практической конференции аспирантов, магистрантов и одарённых студентов, посвященной 50 летному юбилею ТУИТ, Ташкент.







