Единый государственный экзамен (ЕГЭ) — это один из видов государственной итоговой аттестации по образовательным программам среднего общего образования (ГИА), которую пишут все без исключения выпускники одиннадцатых классов российских средних учебных заведений. Первая часть экзамена — это тест, т. е. выбор правильного(-ых) варианта(-ов) ответа(-ов) из нескольких предложенных. Если вы не знаете ответа, вам остаётся положиться на свою интуицию… Однако реально ли получить высокий балл, попросту расставляя ответы наобум?
Ключевые слова: ЕГЭ, теория вероятностей, вероятность сдачи ЕГЭ, экзамен, тест.
Актуальность исследования: данное исследование будет актуально в основном для учащихся 11-х классов, так как оно даст ответ на довольно важный вопрос: насколько хорошо можно написать ЕГЭ, не готовясь к нему? Кажется, как можно «предвидеть» наступление такого случайного события, как правильно данный ответ? Оно ведь может произойти, а может и нет... Но математика нашла способы оценивать вероятность наступления таких событий.
Цель : определить вероятность сдачи ЕГЭ при помощи угадывания правильного ответа, применяя теорию вероятностей
Объект исследования: теория вероятностей
Предмет исследования : практическое применение теории вероятностей
Задачи :
- Изучить задания первой части (теста) из ЕГЭ
- Выявить вероятность сдачи ЕГЭ методом угадывания ответов
Гипотеза : предположим, что невозможно сдать ЕГЭ, просто расставляя ответы в первой части «наугад»
Методы исследования :
- Изучение литературы и других источников информации
- Анализ и синтез
- Идеализация
- Изучение и обобщение
Единый государственный экзамен
Основные сведения о ЕГЭ
Единый государственный экзамен (ЕГЭ) является одним из видов государственной итоговой аттестации (ГИА) по образовательным программам среднего общего образования.
При проведении ЕГЭ используются контрольные измерительные материалы (КИМ), представляющие собой наборы из заданий стандартизированной формы, а также специальные бланки для оформления ответов на задания.
Чтобы получить аттестат, выпускникам необходимо сдать ЕГЭ по двум обязательным предметам — русскому языку и математике (базового или профильного уровня). ЕГЭ по остальным учебным предметам они сдают по своему выбору.
Структура ЕГЭ
Задания ЕГЭ (КИМы) разрабатываются Федеральным институтом педагогических измерений [6].
Примерная структура, форма и содержание КИМов предопределены и не могут быть изменены произвольным образом, а регламентируется они тремя документами, утверждаемыми Рособрнадзором каждую осень: кодификаторами, спецификациями и демоверсиями экзаменов. КИМы включают в себя задания с кратким и развернутым ответами.
В экзаменах по математике базового и профильного уровней нет заданий с выбором ответа: следовательно, для сдачи данных экзаменов способ расстановки ответов «наугад» не подходит меньше всего.
При проведении ЕГЭ по иностранным языкам в состав экзамена входит раздел «говорение», устные ответы на задания которого записываются на аудионосители.
Теория вероятностей
Теория вероятностей — это раздел математики, который изучает числовые характеристики вероятности появления некоторого случайного события в конкретных условиях, которые могут быть многократно воссозданы (как, например, сдача ЕГЭ).
Для событий, вероятность которых находиться по формуле классической вероятности, может быть применён статистический подход. Это было обосновано ещё швейцарским математиком Якобом Бернулли (1655–1705).
Являясь математической основой статистики, теория вероятностей имеет большое значение для множества видов деятельности человека, включающих количественный анализ данных, таких как: социологические исследования, экономический анализ и др.
За последние десятилетия теория вероятностей стала развивающейся наукой со множеством возможных направлений применения.
Вероятность события
В так называемых случайных [1] явлениях существуют определённые закономерности. Задачей теории вероятности является установление таких закономерностей.
Классическое определение вероятности: вероятность события А (обозначается Р(А)) равна отношению числа благоприятствующих исходов к числу всех возможных исходов. Т. е. вероятность события А вычисляется по формуле: Р(А)=n/m, где n ≤ m и n, m є N, из чего следует, что 0 ≤ Р(А) ≤ 1. В данной формуле: n — число благоприятствующих исходов, m — число всех исходов испытания.
Однако в нашей жизни встречаются ситуации, где без практики определить число благоприятных исходов очень трудно, а то и вовсе невозможно.
Например, не подбрасывая кнопку много раз, трудно определить, равновозможны ли ее падения на плоскую часть или на иглу. В подобных случаях и используется статистическое определение вероятности.
Статистическая вероятность
Статистическая вероятность — это числовое выражение степени возможности наступления некоторого события (или того, что данное событие не наступит). Одним из способов, помогающих её рассчитать, является использование формулы Бернулли, позволяющей найти вероятность появления события A при нескольких независимых испытаниях.
Чтобы найти, каков шанс наступления события А при помощи формулы Бернулли, нам надо:
– найти общее количество исходов рассматриваемой ситуации;
– найти количество всех возможных исходов, при которых произойдёт событие А;
– найти, какую часть составляют возможные исходы, при которых произойдёт событие А, от общего количества исходов
Определение вероятности сдачи ЕГЭ
Вероятность сдачи ЕГЭ
Согласно нашим наблюдениям, у учащихся старших классов часто возникают мысли, что можно выбрать ответ наугад и при этом получить высокий балл за экзамен. Но так ли это?
Ответить на этот вопрос мы планируем, используя методы из теории вероятностей. А в качестве объекта для анализа мы решили выбрать ЕГЭ по истории, который сдаём сами.
По данному предмету экзамен включает 14 заданий с выбором ответа. Чтобы сдать экзамен, нужно набрать больше или ровно 32 балла.
Определить вероятность сдачи экзамена (о получении «высокого балла» для поступления в вуз, как мы понимаем, речи не идёт) можно по формуле Бернулли.
Если проводится n независимых испытаний, в результате каждого из которых событие A наступает с вероятностью P(A)=p и не наступает с вероятностью q (q=P(А)=1-p). Вероятность того, что в результате n независимых испытаний событие A наступит ровно k раз равна количеству сочетаний из n по k:
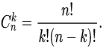
При этом все испытания независимы, а их исходы несовместимы (событие A либо наступает, либо нет). Из этого следует, что вероятность получения удовлетворяющей комбинации будет равна:
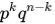
Чтобы найти вероятность того, что в n испытаниях событие A наступит k раз, нужно сложить вероятности получения всех удовлетворяющих комбинаций
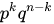
Тогда количество комбинаций равно
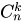
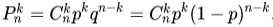
В итоге мы имеем 14 вопросов. Вероятность угадывания правильного ответа на отдельный вопрос одинакова и равна 1/4 = 0.25 (количество удовлетворяющих исходов (дан правильный ответ) ко всем возможным (всего 4 варианта ответа)). Получаем:
P = P(14) = C 14 14 *0.25 14 *0.75 0 = 0,0000000037252902984619140625 — данное число и является числовым выражением вероятности сдачи ЕГЭ методом угадывания правильного ответа.
Заключение
Как мы можем видеть, вероятность сдать ЕГЭ по истории методом случайной расстановки ответов практически равна нулю. Судя по количеству тестовых заданий в ЕГЭ по другим предметам, утверждение, что сдать его методом угадывания правильного ответа невозможно, справедливо для всех предметов, которые доступны для сдачи выпускниками 11-х классов.
Литература:
- Аджиева А. А., Кибишева А. Р. Формула Бернулли // Вестник научных конференций. — ООО Консалтинговая компания Юком, 2016. — №. 4–3. — С. 17–18.
- Википедия [электронный ресурс] // Единый государственный экзамен URL: https :// ru . wikipedia . org / wiki / Единый _ государственный _ экзамен
- Википедия [электронный ресурс] // Формула Бернулли URL: https :// ru . wikipedia . org / wiki / Формула _ Бернулли
- Википедия [электронный ресурс] // Бернулли, Якоб URL: https :// ru . wikipedia . org / wiki / Бернулли ,_ Якоб
- 4ege [электронный ресурс] // Шкала перевода баллов ЕГЭ 2020 URL: https ://4 ege . ru / novosti - ege /4023- shkala - perevoda - ballov - ege . html
- О нас // Федеральный институт педагогических измерений. URL: http://www.fipi.ru/about (дата обращения: 21.03.2020).
[1] Событие называют случайным, если оно либо происходит, либо не происходит










