Покорение космических пространств — давняя мечта человечества. Однако покорение даже ближнего космоса (околоземное пространство) требует больших материальных и энергозатрат. Физические условия в космическом пространстве очень отличаются от тех, с какими сталкивается человек на Земле. Даже при орбитальном движении в околоземном пространстве, например, гравитационное воздействие сводится на нет (состояние невесомости). На орбитальной станции невозможны такие естественные для обычных земных условий явления, как, например, конвекция, горение, стремление к состоянию устойчивого равновесия под действием силы тяжести и др. На человека, на его физиологические процессы отсутствие гравитации (не в смысле гравитационного взаимодействия, а в смысле потери веса) также оказывает огромное влияние. Человек, мечтая о далеких межпланетных путешествиях, должен создавать технику и технологии, применение которых на космическом корабле приближает свойства среды к земным, имитирует их.
Можно говорить, например, о создании искусственной гравитации. Существуют проекты вращающихся вокруг своей оси космических кораблей. Частота вращения должна подбираться таким образом, чтобы возникающие центробежные силы были эквиваленты силе тяжести (т. е. центростремительное ускорение равнялось ускорению свободного падения на Земле). Имитация тяготения Земли может быть основана и на других видах взаимодействия. Например, магнитном или электростатическом.
Рассмотрим более подробно случай электростатического взаимодействия для имитации земных условий на примере математического маятника (рис. 1).
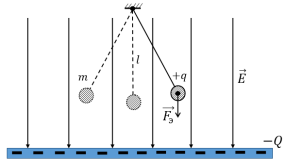
Рис. 1. Математический маятник в однородном электростатическом поле заряженной пластины
Пусть имеется состояние невесомости. Небольшой шарик, имеющий массу
m
и заряд +
q
, находится в однородном электростатическом поле, создаваемом равномерно зяряженной отрицательным зарядом –
Q
пластиной. Т. е. напряженность поля
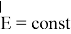
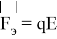
При отклонении шарика от положения равновесия он начнет совершать колебания и, таким образом будет представлять собой математический маятник.
Период математического маятника в поле силы тяжести:
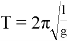
где
g
— ускорение свободного падения (ускорение силы тяжести
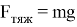
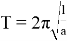
где a — ускорение, получаемое под действием силы электростатического взаимодействия
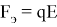
Использовав второй закон Ньютона (
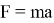
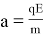
В результате получаем выражение для периода в виде
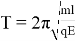
Подобрав заряд шарика и/или напряженность электрического поля таким образом, чтобы
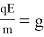
Однако в «обычных», земных условиях (при отсутствии невесомости) от действия силы тяжести не избавиться. Поэтому маятник будет находиться при взаимном действии гравитационного и электростатического полей (рис. 2).
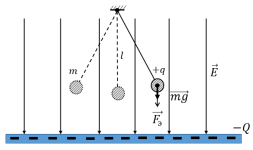
Рис. 2. Математический маятник в однородном электростатическом поле заряженной пластины и гравитационном поле Земли
В этом случае
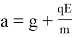
В результате выражение для периода математического маятника в этом случае будет иметь вид
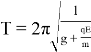
Данная модель может использоваться для измерения напряженности электрического поля или определения электрического заряда (при известных значениях прочих параметров):
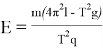
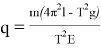
Основное достоинство данной измерительной системы — относительная простота и, несмотря на это, достаточно высокая точность измерений. Несложные прямые измерения периода колебаний при заданных (известных) значениях остальных параметров, входящих в (9) и (10), позволяют косвенно определить значения электрических величин. Другими словами, выполняя механические опыты, проводим электроизмерения.









