Генерация случайных чисел слишком важна, чтобы оставлять ее на волю случая.
Р. Кавью, ORNL
Орёл или решка? Иногда человек при некотором выборе полагается на волю случая. А кто-то живет идеей сорвать «большой куш» в различные лотереи. В последнее время социальные сети пестрят розыгрышами призов, где счастливчики определяются с помощью онлайн-генераторов случайных чисел.
В век цифровых технологий последовательности случайных чисел широко используются в различных направлениях деятельности человека: в компьютерном программировании, в имитационном моделировании, в криптографии. Как ни странно, но актуальным вопросом является привлечение «случайности» для защиты информации в сфере информационной безопасности, а именно, для генерации паролей, создания криптографических ключей. Поэтому задача создания хороших генераторов и эффективных методов их оценки представляет большой интерес.
Меня, как любителя тестирования компьютерных программ с помощью рандомных числовых массивов, заинтересовал вопрос природы случайных чисел. Как формируются последовательности? Есть ли вероятность предугадать такие числа? Если на последний вопрос можно ответить положительно, то можно ли говорить об эффективности кодирования информации, полагаясь на случайные последовательности.
Цель исследования: выявить отсутствие зависимости между числами в последовательности, созданной рандомным генератором.
Задачи:
- Изучить литературные и интернет-источники по теме.
- Выяснить значимые показатели надежности числовых последовательностей на предмет независимости.
- Определить способы тестирования числовых последовательностей
- Оценить надежность выбранных генераторов случайных чисел с помощью проверки свойств последовательности чисел.
Гипотеза: возможно, существует определенная закономерность в последовательности чисел, при их формировании рандомным генератором.
Объект: генераторы рандомных чисел.
Предмет: зависимость и предсказуемость в последовательности случайных чисел
Методы: сравнение, анализ, частично-поисковый; корреляционный анализ, графический анализ гистограммы распределения.
Случайная величина. Классификация генераторов случайных чисел
Существует строгое определение для случайной величины. Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать [1].
Под генератором случайных или псевдослучайных чисел понимается любая программа или устройство, которое с достаточно высокой вероятностью будет производить случайные числа или последовательности случайных чисел, описать которые какими-либо закономерностями, по крайней мере, затруднительно, если не невозможно.
Человека, в качестве надежного генератора случайных чисел, рассматривать нельзя. Распознать «человеческую последовательность» довольно просто, достаточно построить гистограмму распределения чисел и рассмотреть ее с точки зрения равномерности появления числа в последовательности. Компьютер может справиться с такой задачей намного лучше.
Выделяют два основных класса генераторов случайных последовательностей [2]:
– генераторы истинно случайных последовательностей;
– генераторы псевдослучайных последовательностей.
Генераторы истинно случайных последовательностей основываются на различных физических процессах и явлениях, имеющих случайную природу. Примером источника настоящих случайных чисел могут являтся физические шумы — детекторы событий ионизирующей радиации, шум в резисторе, космическое излучение, радиоактивный распад, разряды молнии и т. п. Но такие способы получения случайных чисел применяются в приложениях безопасности редко [3].
Существует альтернативные способы получения последовательностей случайных чисел, построенных на особенных алгоритмах. Но, поскольку любая программа реализует некоторый детерминированный алгоритм, получить истинно случайные числа только с ее помощью невозможно. В связи с этим Джон фон Нейман отмечал, что каждый, кто использует арифметические методы генерации случайных чисел, безусловно, грешит. Тем не менее, подобные генераторы позволяют строить последовательности, схожие (в идеальном случае — неотличимые) с истинно случайными по своим свойствам, и потому носят название генераторов псевдослучайных последовательностей. Генератор псевдослучайных чисел (ГПСЧ, PRNG(англ.)) — алгоритм, генерирующий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению (обычно равномерному).
Сфера применения случайных чисел
В последнее время спрос на случайные последовательности и генераторы случайных последовательностей с заданными вероятностными распределениями значительно возрос. В связи с этим, за рубежом уже стали появляться научно-производственные фирмы, занимающиеся подготовкой больших массивов случайных чисел.
Последовательности случайных чисел — важные строительные блоки в криптографических алгоритмах. Поскольку такие генераторы применяются во многих криптографических задачах, например формирование случайных параметров и ключей систем шифрования, то требования, предъявляемые к ним, оказываются достаточно высокими. Одним из важных критериев является невозможность предсказать последовательность. Поэтому говорить о надежности генераторов псевдослучайных чисел можно только после определенных статистических тестов.
Широко применяются генераторы случайных последовательностей и в онлайн-сервисах для создания различных паролей, причем существуют как бесплатные, так платные варианты услуг.
При переходе на электронный документооборот очень важна электронная цифровая подпись, которая непосредственно связана с генерацией и применением случайных чисел.
Методы тестирования псевдослучайных последовательностей
Понятно, что оценить на случайность отдельно взятое число, не имеет смысла, поэтому тестируется и оценивается последовательность чисел.
Критерии, которые подлежат обязательной проверке:
– частота вхождения числа в последовательность, отсутствие «предпочтений»;
– отсутствие периодических закономерностей.
Существуют графические и статистические тесты для последовательностей чисел при проведении вероятностного анализа.
К категории графических оносятся тесты, которые можно представить в виде графиков и диаграмм, отражающих характеристики свойств исследуемой последовательности:
– гистограмма позволяет оценить равномерность распределения чисел в последовательности и определить частоту повторения каждого символа;
– распределение на плоскости — применяется для определения зависимости между элементами последовательности;
– проверка на монотонность позволяет определить равномерность, исходя из анализа невозрастающих и неубывающих подпоследовательностей;
– автокорреляционная функция — используется для оценки корреляции между сдвинутыми копиями последовательностей и отдельных подпоследовательностей.
Результаты графических тестов интерпретируются человеком, поэтому на их основе выводы могут быть неоднозначными. Статистические тесты исключают субъективность мнения и опираются на численные характеристики, позволяющие однозначно охарактеризовать случайную последовательности чисел.
Существуют специальные пакеты программ для проверки псевдо последовательностей. Один из наиболее строгих наборов — является тесты diehard — это набор статистических тестов для измерения качества набора случайных чисел.
Выбор генераторов псевдослучайных чисел для анализа числовых последовательностей
От качества работы генератора псевдослучайных чисел, применяемых и в имитационном моделировании, и в информационной безопасности, зависит достоверность и точность результатов. Поэтому последовательность чисел, генерируемая рандомным способом, должна пройти проверку двух типов:
– на равномерность распределения;
– на статистическую независимость.
На данный момент времени нет «официального» тестировщика случайных чисел, существет множество различных наборов. Для качественной оценки последовательности чисел необходимо подобрать и выполнить несколько различных способов проверки.
Для исследования были выбраны три генератора случайных чисел. Онлайн-генератор Рандомус (https://randomus.ru), который формирует последовательности с длинной до 300 чисел и позволяет выполнять копирование выходных данных. Встроенные генераторы систем программирования Pascal и Java (Таблица 1). Также был разработан собственный генератор, на основе арифметической формулы (Приложение 3). Для удобства их использования были написаны программы для вывода результата работы генераторов в отдельные файлы.
Таблица 1
Программные коды генераторов псевдослучайных последовательностей
|
Программа формирования последовательности псевдослучайных чисел на языке программирования Pascal var a: array [1..300] of integer; i:integer; Begin Assign (input, 'random.in'); Assign (output, 'random.out'); Reset (input); randomize; for i:=1 to 300 do begin a [i]:=random(1000); end; Rewrite (output); For i:=1 to 300 do Writeln (output, a [i]); Close (input); Close (output); End. |
|
Программа формирования последовательности псевдослучайных чисел на языке программирования Java public class Main { public static void main(String [] args){ for ( int i = 0; i < 300; i++){ int a = ( int )((Math. random () * 1001)); System. out .println(String. valueOf (a)); } System. out .println(«Job well done!"); } |
|
Генератор, разработанный с помощью языка программирования Java на основе арифметической формулы public class Generator{ private static long x_minus_1 = -1; //randomly generated number private static final double a = 19273562; //Const a private static final double b = 1881787946; //Const b private static final long n = 1236845231; //Const n public static Double generate (){ if( x_minus_1 == -1){ long j = System. currentTimeMillis(); while(j > 100000){ j = j % ((long)Math. pow(10, (String.valueOf(j).length() — 1))); } x_minus_1 = j; } x_minus_1 = ((long) (a * x_minus_1 + b)) % n; return Double. valueOf("0”. + String.valueOf(x_minus_1)); } |
Проверка качества работы генератора случайных чисел
Исходя из того, что один из выбранных генераторов псевдослучайных чисел (онлайн-генератор Рандомус) может за один раз предоставить максимум 300 чисел, то анализ остальных выбранных генераторов проводился на такой же длине последовательности. Вариативность тестирования заключалась в выборе разного диапазона чисел для последовательностей.
Варианты последовательностей:
- 10 последовательностей псевдослучайных чисел из диапазона от 0 до10.
- 10 последовательностей псевдослучайных чисел из диапазона от 0 до100.
- 10 последовательностей псевдослучайных чисел из диапазона от 0 до1000.
Графический способ анализа последовательности псевдослучайных чисел
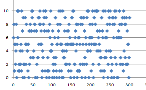
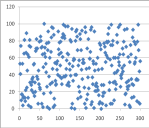
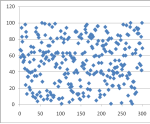
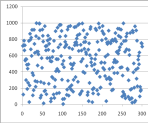
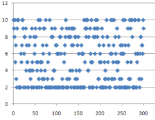
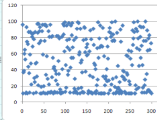
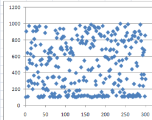
Если сравнить распределение чисел в различных диапазонах на примере онлайн-генератора Рандомус, то можно увидеть, закономерность, чем меньше диапазон выбора случайного числа, тем ярче выражена неравномерность их распределения.
![Пример распределения чисел из диапазона [0,10]](https://moluch.ru/young/blmcbn/2005/2005.001.png)
Рис. 1. Пример распределения чисел из диапазона [0,10]
![Пример распределения чисел из диапазона [0,100]](https://moluch.ru/young/blmcbn/2005/2005.002.png)
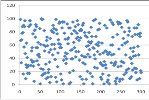
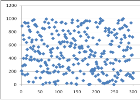
Рис. 2. Пример распределения чисел из диапазона [0,100]
![Пример распределения чисел из диапазона [0,1000]](https://moluch.ru/young/blmcbn/2005/2005.003.png)
Рис. 3. Пример распределения чисел из диапазона [0,1000]
Таблица 2
Выборка результатов тестирования генераторов случайных чисел графическим тестом на равномерность распределения
|
Список тестируемых генераторов: |
Диапазон чисел |
||
|
Равномерность распределения [0,10] |
Равномерность распределения [0,100] |
Равномерность распределения [0,1000] |
|
|
Онлайн генератор https://randomus.ru |
|
|
|
|
Встроенный генератор системы программирования Pascal |
|
|
|
|
Встроенный генератор системы программирова-ния Java |
|
|
|
|
Генератор на Java по формуле |
|
|
|
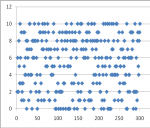
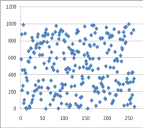
На основе графического представления результатов распределения чисел можно сделать вывод, что первые три генератора псевдослучайных чисел имеют приблизительно равнозначные свойства последовательностей. Что говорит о качестве и надежности генераторов, а генератор, созданный в Java явное неравномерное распределение чисел (рисунок 4).
![Пример распределения чисел из диапазона [0,1000] в генераторе на основе формулы](https://moluch.ru/young/blmcbn/2005/2005.016.png)
Рис. 4. Пример распределения чисел из диапазона [0,1000] в генераторе на основе формулы
Статистический способ анализа последовательности псевдослучайных чисел
В качестве статистического анализа последовательности случайных чисел был выбран корреляционный метод. Корреля́ция — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). Сила корреляционной связи (интерпретация коэффициента корреляции): сильная: ±0,7 до ±1, средняя: ±0,3 до ±0,699, слабая: 0 до ±0,299.
В таблице МS Exel с помощью корреляционной функции был проведен анализ на предмет зависимости между числами псевдослучайно последовательности. Данные корреляционного метода приведены в таблице 3.
Таблица 3
Результаты тестирования последовательностей случайных чисел методом корреляции
|
Список тестируемых генераторов: |
|||
|
Онлайн генератор https://randomus.ru |
Встроенный генератор системы программирования Pascal |
Встроенный генератор системы программирования Java |
|
|
Корреляционный анализ [0,10] |
-0,06674 —0,06775 0,154334 —0,0251 0,113731 0,162587 0,036581 —0,036256 |
0,04122 —0,02127 0,02341 0,02213 —0,02925 0,12455 0,01648 —0,00351 |
0,047119 0,021311 —0,00036 —0,0881 —0,12521 —0,016 0,086807 0,022473 —0,03762 0,134776 |
|
Корреляционный анализ [0,100] |
0,159114 0,022299 0,095351 0,04158 0,099 |
0,12 —0,0162 0,01249 —0,0126 —0,1212 |
-0,04217 —0,12793 0,028275 —0,09068 0,12703 |
|
Корреляционный анализ [0,1000] |
-0,02192 —0,023 |
-0,0157 0,135693 |
0,180809 0,007254 |
На основе полученных тестов коэффициент корреляции показывает, что зависимости между элементами отдельной последовательности отсутствует. Так как слабая корреляционная связь проявляется при коэффициенте 0,299 до 0. По данным таблицы можно увидеть что, максимальный коэффициент корреляции поднимается до уровня 0,18.
Заключение
Рассмотрев различные генераторы и проанализировав свойства, получаемых с их помощью, последовательностей псевдослучайных чисел, я пришел к следующему выводу: выбранные генераторы создают качественные, с точки зрения отсутствия зависимости между случайными числами в их последовательности. Такие последовательности предугадать невозможно.
Гипотеза о возможности существования определенной закономерности в последовательности рандомных чисел и возможности их угадывания нашла частичное подтверждение на примере одного из четырех тестируемых генераторов случайных чисел.
Исходя из того, что псевдослучайные последовательности применяются для криптографии, то говорить о надежности рассмотренных генераторов для этой сферы сложно. Потому что проведенный анализ рассматривался на небольших последовательностях и проведены только несколько видов тестов, позволяющих сделать достаточно быстро, без особых временных затрат общие выводы о надежности последовательностей.
Литература:
- Григорьев А. Ю. Методы тестирования генераторов случайных и псевдослучайных последовательностей// Ученые записки УлГУ. Сер. Математика и информационные технологии. УлГУ. Электрон. журн. 2017, № 1, с. 22–28
- Рябко Б. Я., Фионов А. Н. Криптографические методы защиты информации: Учебное пособие для вузов. М.: Горячая линия — Телеком, 2005
- https://cyberleninka.ru/article/n/metod-otsenki-kachestva-kriptostoykih-generatorov-psevdosluchaynyh-posledovatelnostey/viewer — метод оценки качества криптостойких генераторов псевдослучайных последовательностей
- https://ru.wikipedia.org/wiki — свободная энциклопедия