При обмене электронными документами по каналам связи возникает проблема аутентификации как автора документа, так и самого документа. Это означает, что получатель должен быть уверен, во-первых, в истинности автора, а во-вторых, в отсутствии изменений в самом документе. В обычных бумажных документах эти проблемы решаются за счет того, что содержание документа и рукописная подпись автора жестко связаны физическим носителем данных (бумагой). В электронных документах на машинных носителях такой связи нет.
Целью аутентификации электронных документов является их защита от возможных видов вредоносных действий:
– активный перехват — злоумышленник, подключившись к каналу связи, перехватывает файлы документов и меняет их на другие,
– маскарад — абонент
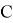
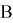
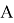
– ренегатство — абонент
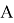
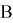
– подмена — абонент
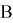
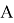
– повтор — абонент
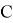
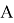
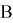
Один из самых простых способов аутентификации (подписи) электронных документов — использование шифрования. При этом отправитель
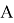
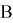
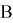
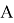
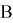
Именно поэтому для аутентификации электронных документов, передаваемых по телекоммуникационным каналам связи, используется специально создаваемая электронная цифровая подпись (ЭЦП). Функционально ЭЦП аналогична обычной рукописной подписи и обладает следующими свойствами:
– показывает, что подписанный документ получен от лица, поставившего свою подпись;
– не дает возможности лицу, поставившему свою подпись, отказаться от подписанного документа;
– является неотъемлемой частью данного документа и не может быть использована для подписания другого документа;
– гарантирует целостность подписанного документа.
Электронная цифровая подпись представляет собой относительно небольшое количество дополнительных цифровых данных, которые передаются вместе с подписанным текстом. Применение ЭЦП имеет вид следующего криптографического протокола:
1) для документа
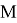
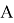
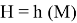
2) хэш-значение
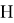
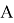
3) зашифрованное хэш-значение вместе с документом
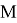
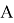
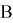
4) получатель
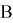
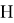
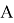
Если два полученных хэш-значения совпадают, то подпись отправителя
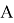
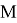
Участники криптографического протокола ЭЦП должны предварительно договориться об использовании определенной криптографической системы, а также хэш-функции.
Среди большого количества различных асимметричных криптосистем самой популярной является криптосистема RSA, разработанная в 1977 г. и получившая свое название в честь Рона Ривеста (Rivest), Ади Шамира (Shamir) и Леонарда Эйдельмана (Adleman). Алгоритм RSA используется в банковских компьютерных сетях, особенно для работы с удаленными клиентами (Обслуживание кредитных карточек). Надежность алгоритма основывается на трудности факторизации (разложения на множители) больших чисел и трудности вычисления дискретных алгоритмов (нахождения
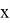
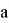
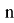
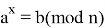
Алгоритм RSA состоит из трех частей: генерации ключей, шифрования и дешифрования. Генерируют
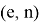
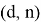
Хэш-функция
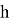
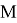
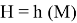
Основные свойства хэш-функции:
1) хэш-значение
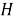
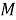
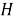
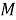
2) хэш-значение
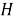
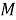
3) хэш-функция
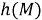
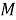
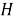
4) вероятность того, что хеш-значения двух разных документов совпадут, чрезвычайно мала.
Подавляющее большинство используемых хэш-функций имеют вид
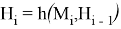
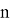
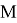
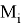
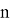
Содержание указанных входных значений хэш-функции следующее:
1) первое входное значение представляет собой очередной блок документа
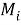
2) второе входное значение представляет собой хэш-значение
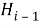
При исчислении хэш-значение для первого блока
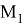
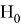
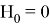
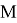
Правило образования одного хэш-значения из двух входных зависит от типа хэш-функции. В простейшем случае здесь может использоваться сложение по модулю 2, т. е.
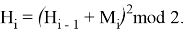
Покажем реализацию алгоритма создания и передачи ЭЦП на примере. Для создания иллюстративного примера мы будем использовать небольшие числа в десятичной форме записи. Найдем хеш-образ фамилии Трубникова, используя хеш-функцию
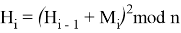
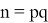
Возьмем два простых числа
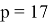
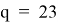
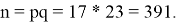
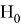
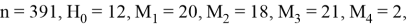
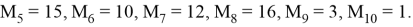
Используя формулу
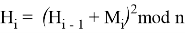
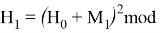
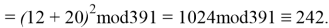
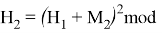
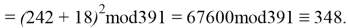
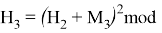
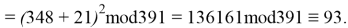
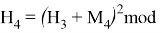
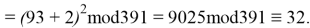
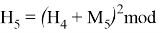
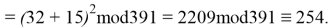
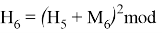
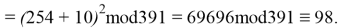
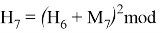
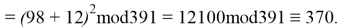
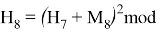
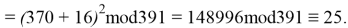
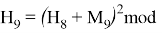
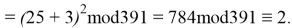
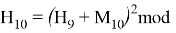
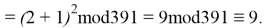
В итоге получаем хеш-образ сообщения «ТРУБНИКОВА», равный 9, который будем использовать для вычисления электронной цифровой подписи по схеме RSA.
Сгенерируем открытый и секретный ключи для алгоритма шифрования RSA. Оставим ранее выбранные простые двузначные числа
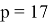
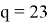
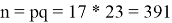
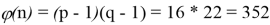
Секретный ключ
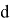
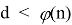
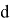
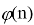
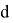
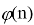
Пусть
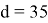
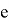
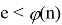
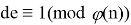
Получим
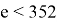
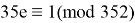
Последнее условие означает, что число
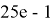
Таким образом, для определения
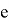
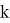
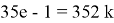
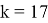
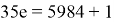
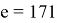
Таким образом мы сгенерировали
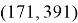
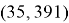
Электронная цифровая подпись сообщения, состоящего из Фамилии, вычисляется по правилу
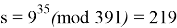
Для проверки ЭЦП используем открытый ключ
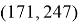
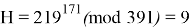
Как видим, хеш-образ сообщения совпадает с найденным значением H, следовательно, подпись признается подлинной.
Таким образом мы построили демонстрационный пример создания электронной цифровой подписи с использованием хеш-функции
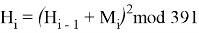
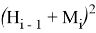
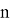
Литература:
- Айерлэнд К. Классическое введение в современную теорию чисел / К. Айерлэнд, М. Роузен. — Пер. с англ. — М.: Мир, 1987. — 416 с.
- Алферов А. П. Основы криптографии / А. П. Алферов, А. Ю. Зубов, А. С. Кузьмин, А. В. Черемушкин. М.: Гелиос АРВ, 2002. — 480 с.










