В статье авторы приводят игру на бумаге, на примере которой сформулированы правила движения робота на плоскости. В явном виде приведена функциональная зависимость для классификации возможных маршрутов робота. Приведены результаты расчетов для определения количества необходимых узлов и соединителей на примере конструктора Евтиных.
Ключевые слова: комбинаторика, игра на бумаге, математическое моделирование, игровой конструктор.
Формирование у школьников навыков математического образа мышления и математической интуиции, способность к поиску оригинальных решений учебных и олимпиадных заданий является актуальной задачей. Для решения этой задачи существует огромное количество материалов и приёмов.
Цель работы — расширения игровых возможностей конструктора Евтиных через разработку маршрутов движения робота. Конструктор включает деревянные кубики с отверстиями и соединительные палочки (рис. 1). Элементы конструктора являются открытым игровым материалом, что позволяет воспроизводить многие известные игры и головоломки (например, полимино, куб сома, палочки Кюизенера, ханойская башня) [1], а также придумывать новые оригинальные комбинации как на плоскости, так и в пространстве.
Объектом исследования является создание правил движения робота на плоскости, а предметом — функциональные условия существования маршрутов движения, которые формируются при случайном выборе тройки целых чисел а , b и с .

Рис. 1. Деревянные кубики с отверстиями и соединительные палочки
Предварительные замечания и определения
Для дальнейшего изложения материала мы предлагаем использовать следующую игру на бумаге. Допустим, что у нас есть робот, который помещается в узел клетки тетради. У роботаесть три команды перемещения по границам клетки:
а) сходить прямо на a клеток,
б) сходить прямо на b клеток и
в) сходить прямо на с клеток.
После каждой команды робот должен повернуть направо, то есть на 90⁰. Робот должен вернуться в исходный узел, для этого он должен повторить указанные выше команды четыре раза. Поскольку маршрут замкнутый, порядок выполнения указанных команд не имеет значения. Поэтому для определенности будем считать
a
≤
b
≤
c
. Для генерации чисел
a
,
b
и
c
будем использовать игральную кость (кубик), тогда 1 ≤
a
≤
b
≤
c
≤ 6 и существует 6
3
=216 возможных вариантов, которые можно получить при трех бросках кубика. Проанализировав всевозможные тройки чисел (
a
,
b
,
c
), мы выделили комбинации
a
,
b
и
c
, которые определяют различные типы маршрутов. Мы назвали их —
квадрат
,
крест
,
решетка
,
мельница,цветок
и
клевер
(рисунок 2). На рисунке 2, если узел посещен справа-вниз, справа-вверх, слева-вниз или слева-вверх (то есть угловая точка), то узел обозначен


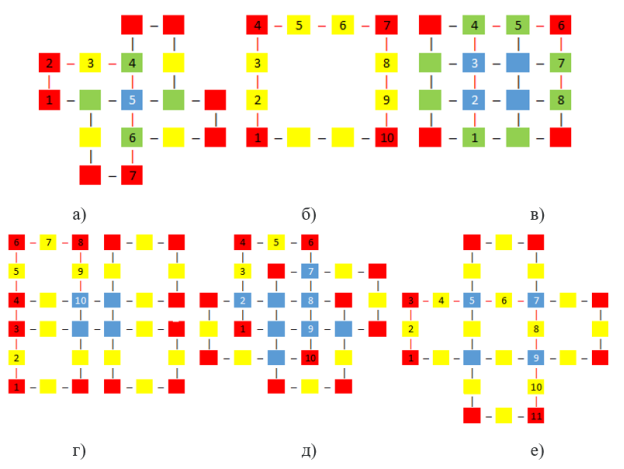
Рис. 2. Примеры маршрутов для различных ( a , b , c ): a) мельница (1, 2, 3), б) квадрат (3, 3, 3), в) решетка (3, 2, 2), г) клевер (5, 2, 2), д) цветок (3, 2, 4), е) крест (2, 4, 4)
Как и следовало ожидать, самым редко встречаемым оказался маршрут квадрат , который может быть получен только при a = b = c . Всего возможно 6 различных вариантов: (1, 1, 1), (2, 2, 2), (3, 3, 3), (4, 4, 4), (5, 5, 5) и (6, 6, 6). Статистический ряд для всех маршрутов представлен в таблице 1.
Таблица 1
Статистический ряд для маршрутов
|
Маршрут |
Частота |
|
квадрат |
6 |
|
клевер |
18 |
|
клевер_2 |
42 |
|
крест |
45 |
|
решетка |
18 |
|
мельница |
45 |
|
цветок |
42 |
|
Всего |
216 |
В таблице 1 мы выделили маршруты клевер и клевер_2 , которые отличаются геометрией движения, однако с точки зрения дальнейшего анализа эти маршруты не содержат существенных отличий.
Для достижения поставленной цели требуется решить две задачи: 1) определить количество различных узлов — угловых, сквозных, смешанных и центральных и 2) определить количество посещенных границ клеток для произвольных a , b и c .
Для поиска решения первой задачи — определить количество различных узлов — угловых, сквозных, смешанных и центральных — необходимо записать правила, по которым возможно классифицировать маршрут (рис. 2) через некую функцию от a , b и c . Мы предлагаем записать явный вид этой зависимости в следующем виде:

Далее мы реализовали функцию (1) в MS Excel с использованием встроенных функций ЕСЛИ(), И() и ИЛИ():

В приведенных выше формулах мы использовали именованные области, которые для удобства назвали a, b и c соответственно. Мы не стали объединять все функции ЕСЛИ() в одну ячейку, потому что это существенно усложняет процесс тестирования результата вычислений, а вместо этого предлагаем использовать функцию СЦЕПИТЬ(), которая будет выводить на экран результат работы (одно слово) — тип маршрута для произвольных целых чисел a , b и c .
Заметим, что количество смешанных и центральных узлов для каждого маршрута — постоянная величина, а количество сквозных и угловых узлов для каждого маршрута это функция, которую мы также выразили через a , b и c . Из таблицы 2 видно, что особого подхода потребовал анализ комбинаций для маршрутов мельница и крест , в частности для троек вида (1, 1, 2) и (2, 2, 3). Это связано с тем, что потребовалась особая обработка для вычисления количества угловых и сквозных узлов.
Таблица 2
Расчетные формулы для определения количества различных узлов
|
Маршрут |
Количество узлов |
|||
|
|
|
|
|
|
|
квадрат |
4 |
=4*(a − 1) |
0 |
0 |
|
клевер |
12 |
=4*(2*a + c − 5) |
0 |
4 |
|
клевер_2 |
12 |
=4* (2*a + c − 5) |
0 |
4 |
|
крест |
8 |
=ЕСЛИ(a=1; 8*(b — 2); 4*(2*a+2*b — 7)) |
0 |
4 |
|
решетка |
4 |
=4*(c − 3) |
8 |
4 |
|
мельница |
=ЕСЛИ( a =1; 4;8) |
=ЕСЛИ(И(a=1; b=1); 0; ЕСЛИ(a=1; 4*(2*b-3); 4*(2*a+2*b-5))) |
4 |
1 |
|
цветок |
12 |
=4* (а + b + c — 7) |
0 |
12 |
Для решения второй задачи можно воспользоваться теоремой Эйлера (Лемма «о рукопожатиях») [2], которая звучит следующим образом. Сумма степеней всех вершин графа является четным числом и равна удвоенному числу его ребер. В нашем случае маршруты, приведённые на рисунке 2, представляют собой графы, где узлы клеток соответствуют вершинам графа, а границы клеток — ребрам графа. Также отметим, что для вершин графа мы можем указать их степени: угловая , сквозная — 2, смешанная — 3, центральная — 4. Тогда для вычисления количества соединителей можно использовать формулу:
=(2*(red+yellow)+3*green+4*blue)/2,
здесь red, yellow, green,blue обозначают именованные области для хранения количества угловых, сквозных, смешанных и центральных узлов соответственно.
Выводы
В статье приведены правила игры и результаты комбинаторных расчетов для определения количества различных узлов — угловых, сквозных, смешанных и центральных и посещенных границ клеток для произвольных a , b и c . В MS Excel разработана программа для автоматического определения типа маршрута и количества необходимых элементов из игрового конструктора Евтиных. Разработанная программа требует от пользователя только ввода трех целых чисел a , b и c . В дальнейшем планируется разработать мобильное приложение, в основу которого будут положены полученные результаты. В нашем исследовании мы наложили условия 1 ≤ a ≤ b ≤ c ≤ 6, тем самым ограничили область поиска для маршрутов. Это ограничение продиктовано тем, что конструктор Евтиных имеет конечный набор деталей. Однако рассуждения, приведённые в тексте статьи, могут быть применены и для произвольных a , b и c .
На основании полученных результатов можно сделать вывод, что образовательные возможности игрового конструктора расширяются и теперь можно продемонстрировать решения следующих классов задач: «Докажите, что робот, двигаясь по указанным выше правилам, всегда будет возвращаться в исходную точку», «Сколько нужно использовать деталей, чтобы сконструировать маршрут робота при а =3, b =4, c =5?", «Верно ли утверждение, что синих деталей потребуется больше чем красных, если маршрут определяется тройкой (2, 3, 4)?".
Авторы выражают благодарность П. Евтину, учителю школы № 49 г. Томска за предоставленный набор для проведения экспериментов.
Литература:
- Лучшая книга логических игр и головоломок для самых умных: язык; математика; природа; общество / пер. с исп. О. Г. Мунтяновой. — Москва: Издательство АСТ, 2015. — 240 с.
- Гуровиц В. М., Ховрина В. В. Графы. — М.: МЦНМО, 2014. — 32 с.