В данной статье рассматривается вывод формулы квадрата длины биссектрисы в произвольном треугольнике. Вывод формулы разными способами даёт возможность учащимся повторить широкий спектр геометрических фактов, совершенствовать навыки применения разных методов и приёмов решения задач, способствует более глубокому и прочному пониманию и запоминанию материала.
Ключевые слова: биссектриса, длина, произвольный треугольник.
Математика — это искусство называть разные вещи одним и тем же именем.
А. Пуанкаре
Когда-то геометрия олицетворяла всю математику. Геометрия, как и всякая наука, возникла под влиянием жизненных потребностей. Необходимость их повседневного удовлетворения ставит человека перед целым рядом вопросов о форме окружающих его предметов, вычислениях, связанных с землемерием, строительным делом и т. д. Первые геометрические понятия возникли в доисторические времена. Человек не только пассивно наблюдал природу, но и практически осваивал и использовал её богатство. Имеются вполне достоверные сведения о значительном развитии геометрических знаний в Египте более чем за две тысячи лет до нашей эры. Материальные потребности побуждали людей изготовлять орудия труда, обтёсывать камни и строить жилища, лепить глиняную посуду и натягивать тетиву на лук. Люди натягивали свои луки, изготавливали разные предметы с прямыми рёбрами и постепенно дошли до отвлечённого понятия прямой линии. Узкая плодородная полоса земли между пустыней и рекой Нил ежегодно подвергались затоплению, и каждый раз разлив смывал границы участков, принадлежащих отдельным лицам. После спада воды требовалось с возможно большей точностью восстановить эти границы, ибо каждый из участков ценился весьма высоко. Это заставило египтян заниматься вопросами измерения, то есть землемерием. Помимо этого, они вели развитую торговлю и поэтому нуждались в умении измерять ёмкость сосудов. Искусство кораблевождения привело их к астрономическим сведениям. Выдающиеся постройки египтян — пирамиды, которые сохранились до нашего времени, свидетельствуют, что их сооружение требовало знания пространственных форм. Всё это указывает на чисто опытное происхождение геометрии.
Практическая деятельность человека служила основой длительного процесса выработки отвлечённых понятий, открытия простейших геометрических зависимостей и соотношений. Со времён, когда накопилось большое количество геометрических фактов, у людей появилась потребность обобщения, уяснения зависимости одних элементов от других, установления логических связей и доказательств. Геометрия стала наукой лишь после появления в ней теорем и доказательств.
К числу основных геометрических фактов следует отнести и теорему о квадрате длины биссектрисы угла произвольного треугольника. Эта теорема часто используется при решении геометрических задач.
Биссектриса это очень интересная, удивительная и замечательная линия в треугольнике. Поэтому и к числу основных геометрических фактов следует отнести и теорему о том, что биссектриса делит противоположную сторону треугольника в отношении прилежащих сторон.
Из различных источников Интернета известна формула квадрата длины биссектрисы произвольного треугольника (рис.1):
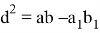
- Через вписанные углы.
- Через теорему косинусов.
- Через теорему Стюарта.
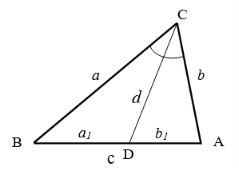
Рис. 1
Предлагается четвёртый способ доказательства этой теоремы.
Теорема. Квадрат длины биссектрисы произвольного треугольника равен разности произведения образующих его сторон и произведения отрезков, на которые биссектриса делит третью сторону треугольника.
Доказательство. В произвольном ∆
АВС
биссектриса угла
С
обозначается
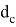
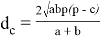
где p — полупериметр.
Возведём обе части выражения (1) в квадрат и с учётом, что
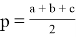
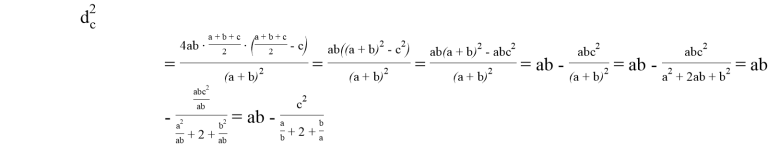
По свойству биссектрисы внутреннего угла треугольника АВС имеем:
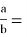

где a 1 , b 1 — отрезки стороны АВ=с .
Из выражений (2) и (3) найдём квадрат биссектрисы:
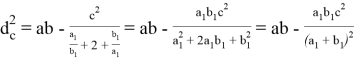
Используя выражение (4) с учётом, что
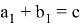
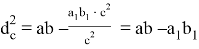
А теперь сформулируем теорему о квадрате длины биссектрисы в треугольнике иначе.
Теорема.
Квадрат длины биссектрисы треугольника равен произведению суммы двух сторон одного треугольника и разности двух сторон другого, на которые он разделён биссектрисой (рис.1):
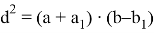
Доказательство. Воспользуемся формулой квадрата длины биссектрисы произвольного треугольника:
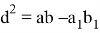
Биссектриса CD делит треугольник АВС на два треугольника: ∆ АСD и ∆ ВСD . По свойству биссектрисы внутреннего угла ∆ АВС будем иметь:
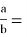

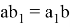
Сложив выражения (5) и (6), получим:
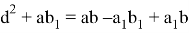
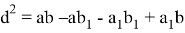
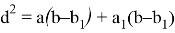
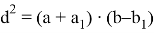
Задача 1. В треугольнике AВC известно, что a=9см, b=6см, с=12см . Из вершины угла C проведена биссектриса CD . Найти длину биссектрисы CD (рис.1).

Ответ:
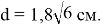
Задача 2.
В треугольнике
AВC
из вершины угла
C
проведена биссектриса
CD
, которая делит сторону
АВ
в
отношении
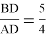

Ответ:
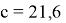
Учитель, приучая учащихся к самостоятельному поиску доказательства, поощряя их работу в этом направлении (даже, если найденное доказательство сложнее известного), может добиться более прочных и глубоких знаний, способствовать повышению интереса к предмету.
Обучение учащихся доказательству теорем зачастую оказывается малоэффективным. Одна из причин этого, на мой взгляд, отсутствие возможности у авторов школьных учебников представлять различные способы доказательства той или иной теоремы. Следовательно, для активизации познавательной деятельности учащихся и для повышения логического уровня их мышления, учителю необходимо ставить перед учащимися проблему поиска различных способов доказательства одной и той же теоремы. Учитель должен на примере показать, как это делается. Затем перед учителем возникает проблема побудить у учащихся желание самостоятельно искать различные способы доказательства теорем.
Таким образом, отыскание различных способов доказательства одной и той же теоремы — важнейшее средство развития творческого мышления учащихся.
Литература:
- Выгодский М. Я. Справочник по элементарной математике. Москва. «Наука». 1986.
- Некрасов В. Б. Школьная математика. Санкт-Петербург. «Авалон». 2006.
- Научно-исследовательская работа по теме «Биссектриса угла треугольника». Учащийся: Александров А. А. Научный руководитель: Чуканова И. И. Республика Татарстан. Бугульма, 2012.







