Комплексные числа: возможности самостоятельного изучения



В данной статье рассматривается вопрос возможности самостоятельного изучения учащимися темы «Комплексные числа». Исследуется вопрос об их применимости в алгебре и началах математического анализа. Представляется решение, позволяющее осуществить самостоятельный экскурс в мир комплексных чисел.

Комплексные числа — важнейшая тема курса математики. Она не только имеет большое значение в современной науке, но и входит в программу обучения большинства вузов, в том числе и без технической направленности. Несмотря на это, ознакомление с темой происходит только на последнем году школьного обучения, в 11 классе. Кроме того, данной темы нет в Едином Государственном Экзамене, а значит есть риск, что время, выделенное на изучение комплексных чисел, теоретически может быть сокращено в пользу подготовки выпускников к экзамену. В таком случае школьники ознакомятся с этой важной и интересной темой лишь поверхностно, либо уже в вузе. Таким образом, знания школьников о числовых множествах ограничиваются действительными числами, а это сказывается как на решении конкретных задач, так и на математическом кругозоре учеников.

Что такое комплексные числа, чем они отличаются от действительных и как может быть применена теория комплексных чисел — вопросы, которые легли в основу проводимого нами исследования.

При изучении истории числовых множеств важно понимать, что их развитие всегда требовало много времени. Даже отрицательные числа когда-то были чужды математикам и требовали подробного изучения.

Можно сказать, что история комплексных чисел начинается с XVI века, когда началось подробное изучение кубических уравнений. Для их решения итальянским ученым Дж. Кардано была выведена общая формула для решения кубического уравнения :

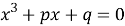
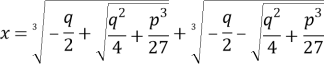
В случае, если уравнение имеет единственный действительный корень, проблем не возникает. При этом если уравнение имеет три, пусть и действительных, корня, для их нахождения потребуется извлечь квадратный корень из отрицательного числа. Таким образом перед математиками встала проблема: почему для получения действительных корней уравнения требуется применение невозможной операции извлечения корня из отрицательного числа? Для ее решения в 1545 г. Дж. Кардано предложил ввести новые числа вида , названные «чисто отрицательными» или «софистически отрицательными». Ученый считал, что вычисления с ними должны производиться по правилам обычной алгебры:

. И, хотя сам Кардано старался избегать применения новых чисел, это стало важным шагом к расширению множества действительных чисел.

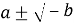
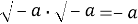
Изначально новые числа были восприняты с настороженностью, а некоторые математики считали, что результаты исследований, полученные с их помощью, недостоверны и требуют дополнительных доказательств. Несмотря на это изучение чисел продолжалось, и в 1572 г. итальянский математик Р. Бомбелли установил первые правила арифметических операций. В 1637 году Р. Декарт ввел название «мнимые числа», а в 1777 г. Л. Эйлером был введен символ (первая буква фр. Imaginaire — «мнимый»). Во всеобщее употребление символ вошел благодаря К. Гауссу. Со временем комплексные числа развивались и применялись математиками все чаще. В 1748 г. Л. Эйлер вывел формулу , которая связывает показательную и тригонометрические функции. Кроме этого, она позволяет находить синусы и косинусы от комплексных чисел, вычислять их логарифмы, т. е. строить теорию функций комплексного переменного. К концу XVIII века комплексные числа полностью вошли в обиход математиков. Их начали применять для выражения корней линейных дифференциальных уравнений с целыми коэффициентами, которые встречаются в теории колебаний материальной точки в сопротивляющейся среде. Швейцарский математик Я. Бернулли применил комплексные числа для вычисления интегралов. В течение XVIII века с их помощью были решены многие прикладные задачи, связанные с картографией и гидродинамикой, но только к началу XIX века было получено геометрическое изображение комплексных чисел. Независимо друг от друга математики Г. Вессель, Ж. Арган и К. Гаусс предложили представлять комплексные числа точками на плоскости. Позднее оказалось, что комплексному числу удобнее сопоставить вектор, выходящий из начала координат. Геометрическое представление еще более расширило область применения комплексных чисел. Их стали применять в вопросах, где величины также изображаются векторами на плоскости, т. е. при изучении течения жидкости, в задачах теории упругости. В советском союзе изучением теории функции комплексного переменного занимались ученые Н. И. Мусхелишвили, М. В. Келдыш, М. А. Лаврентьев. Н. Н Боголюбов и В. С. Владимиров занимались ее применением в квантовой теории поля.

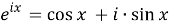
Таким образом, комплексные числа стали достаточно популярны и в настоящее время широко применяются в науке.

Вопрос самостоятельности изучения теории комплексных чисел побудил нас к поиску решения, которое бы позволило наглядно представить информацию по теме и сделать ее доступной для всех интересующихся. Таким решением стало создание онлайн-курса.

Анализ различных цифровых сервисов позволил выявить и сравнить платформы, наиболее пригодные для его создания. В таблице 1 представлена сравнительная характеристика отобранных цифровых сервисов.

Таблица 1

	wizer.me	geogebra.org	wordwall.net	quizizz.com
Возможность добавлять свои материалы	+	+	+	+
Обязательная регистрация	+	-	+	-
Бесплатность	-	+	-	+
Возможность размещать как теоретический материал, так и задания	+	+	-	-
Наглядность представления информации	+	+	Возможно представление только в виде тестовых заданий	Возможно представление только в виде тестовых заданий
Структурированность представления информации	Возможно создание краткого конспекта	+	Возможно представление только в виде тестовых заданий	Возможно представление только в виде тестовых заданий

По данным таблицы видно, что для размещения обучающего курса наиболее подходящей является платформа geogebra. Ее главное отличие заключается в том, что пользователь может разместить большой объем информации, структурировать материал, а также добавить в работу необходимые графики, построения и схемы. При необходимости их можно сделать интерактивными, чтобы пользователи могли взаимодействовать с материалом.

Далее была определена структура курса. Онлайн-курс состоит из двух частей, первая — теоретическая, в ней приведены все необходимые для изучения темы термины, такие как:

— определение комплексного числа;

— геометрическая интерпретация комплексного числа;

— модуль комплексного числа;

— сопряженное к числу и свойства сопряженных;

— аргумент комплексного числа.

Кроме этого, рассмотрены формы записи комплексных чисел: алгебраическая, тригонометрическая и показательная.

Вторая часть — практическая. В ней рассмотрены арифметические действия с комплексными числами. Каждая из частей состоит из нескольких разделов, каждый из которых оканчивается интерактивным графиком и несколькими небольшими заданиями к нему.

Например, в разделе, посвященному умножению комплексных чисел, содержатся задания на доказательство, которые можно выполнить с помощью графика: «Докажите, что: 1) при перемножении комплексных чисел их модули перемножаются, а аргументы складываются; 2) при умножении комплексного числа на действительное получается комплексное число; 3) результат умножения сопряженных — всегда действительное число (сопряженные симметричны относительно оси абсцисс); 4) что .

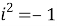
На основании изученной теории, запроса учащихся, студентов — потенциальных потребителей был создан онлайн-курс, размещенный по ссылке: https://www.geogebra.org/m/kxxrqtvv

По результатам проведенного в ходе апробации курса опроса был сделан вывод о соответствии продукта критериям: понятность, полнота изложения информации, структурированность, удобство интерфейса, бесплатность. Также большинство участников отметили, что планируют использовать продукт проекта при изучении комплексных чисел в 11 классе. Это обосновывает актуальность исследования, а также показывает, что проблема, поставленная в начале работы, может быть решена с помощью итогового продукта.

Таким образом, данная исследовательская работа поможет ученикам расширить свой математический кругозор, а также может повысить интерес к самому предмету, а продукт проекта будет способствовать самостоятельному изучению комплексных чисел школьниками.

Литература:

1. Алгебра и геометрия комплексных чисел [Статья]/ авт. А. Канунников // Квант. — Май 2017 г. — стр. 28–31, 34.
2. Алгебра и начала математического анализа. 11 класс [Книга] / авт. Пратусевич М. Я. Столбов К. М., Головин А. Н.. — [б.м.]: Издательство «Просвещение», 2010.
3. Гиперкомплексные числа [Книга] / авт. Кантор И. Л. Солодовников А. С.. — [б.м.]: Издательство «Наука», 1973.
4. Изучение комплексных чисел в общеобразовательной школе [Статья] / авт. Жмурова И. Ю. Баринова С. В. // «Молодой ученый». — Январь 2020 г.. — стр. 312–314.
5. Комплексные числа [Статья] / авт. С. Дориченко // Квант. — Сентябрь/Октябрь 2008 г.- стр. 11–18.
6. Комплексные числа [Статья] / авт. Ю. Соловьев // Квант. — 1991 г.. — № 7. — стр. 47–54.
7. Магия комплексных чисел [Статья] / авт. А. Канунников // Квант. — Май 2017 г. — стр. 5–11.