В статье автор рассматривает применение формул Виета как универсального способа решения уравнений степени n. Представляется созданный автором уникальный онлайн тренажер как способ самостоятельной подготовки к решению олимпиадных задач, заданий ЕГЭ с использованием формул Виета.
В заданиях ЕГЭ и олимпиадных задачах часто встречается необходимость решать уравнения n степени и задачи, связанные с ними. На уроках математики часто приходится решать уравнения n степени и различные основанные на них задачи, но некоторым способам их решения уделяется недостаточно внимания при изучении, из-за чего они не используются учениками.
В школе ученики достаточно подробно изучают теорему Виета для квадратных уравнений. Однако сфера применения формул Виета значительно шире.
Представим общий вид формул Виета (1), где
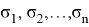
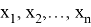
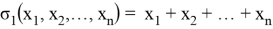
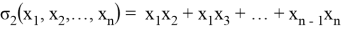
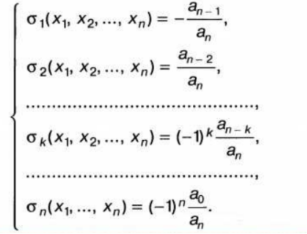
Для того, чтобы упростить решение задач, представим некоторые часто встречающиеся выражения через основные симметрические многочлены:
—
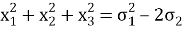
—
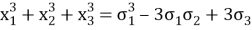
—
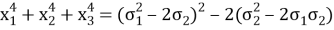
Анализ дополнительной литературы позволил составить подробные алгоритмы решения уравнений 3 и 4 степени с помощью теоремы Виета. В ходе анализа также было отмечено, что данный способ применим только к уравнениям, имеющим целые корни.
Рассмотрим алгоритм решения уравнения вида
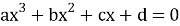
1) найти один корень уравнения подбором;
2) используя формулы
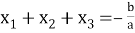
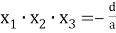
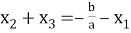
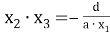
3) найти оставшиеся корни, при необходимости составив вспомогательное квадратное уравнение вида
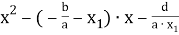
4) записать ответ.
При решении уравнения
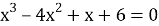
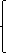
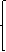
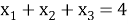
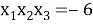
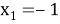
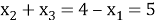
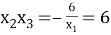
Тогда
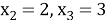
Ответ: 1, 2, 3.
Теперь выделим основные шаги решения задач, связанных с корнями уравнения n степени:
1) определить степень многочлена;
2) записать теорему Виета для выражения необходимой степени;
3) представить данный многочлен через основные симметрические многочлены ;
4) вычислить необходимые значения;
5) записать ответ.
Для
задачи
: «Числа -1 и 2 являются корнями многочлена
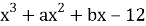
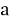
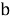
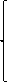
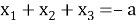
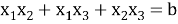
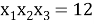
Зная, что
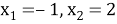
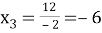
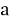
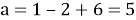
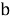
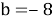
Ответ: 5, -8.
Ситуация обращения к формулам Виета при решении квадратных уравнений и не только побудила нас к поиску сервисов, позволяющих создавать тренажеры. Несколько сетевых сервисов сравнивались по указанным представленным в таблице критериям.
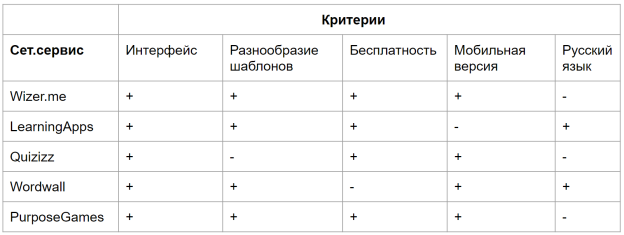
Для создания тренажера был выбран сервис Wizer.me, который соответствует наибольшему количеству критериев и является самым удобным. Данный сетевой сервис позволяет создавать разнообразные рабочие листы для практики.
В результате был создан уникальный интерактивный тренажер, направленный на практику в решении уравнений 3 и 4 степени. Тренажер содержит разнотипные задания, которые направлены на отработку ключевых умений данной темы. Успешное выполнение заданий будет являться показателем понимания темы. После отправки ответов вы сразу же можете проверить их правильность.
Ниже представлена краткая инструкция по использованию тренажера:
1) отсканируйте QR-код или перейдите по ссылке (https://app.wizer.me/learn/OGEZ2B) и зарегистрируйтесь;
2) выполните задания;
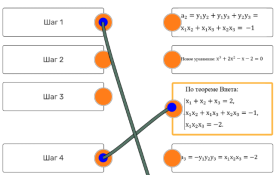
3) сдайте работу;

4) проверьте правильность.
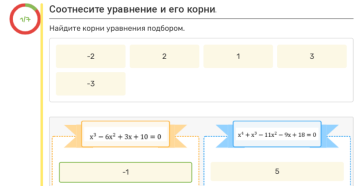
Результаты апробации тренажеры позволили констатировать факт его соответствия заявленной идее. Онлайн-тренажер, действительно, помогает разобраться в теме и дает возможность практиковаться в ней. Интерфейс сайта удобен, а предоставляемая информация понятна и доступна.
Во время разработки проекта стали понятны основные возможности применения теоремы Виета:
— решение уравнений высших степеней;
— решение задач, основанных на поиске корней многочлена степени выше 2;
— использование при решении заданий ЕГЭ и олимпиадных задач.
Созданный тренажер может использоваться учениками для дополнительной практики в данной теме и подготовки к ЕГЭ, а также учителями математики, например, при подготовке учащихся к олимпиадам.
Литература:
- Колягин Ю. М., Ткачева М. В., Федорова Н. Е., Шабунин М. И. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс: базовый и углубленный уровни. М.: Просвещение, 2019. — 384 с.
- Пратусевич М. Я., Столбов К. М., Головин А. Н. Алгебра и начала математического анализа. 10 класс: профильный уровень. М.: Просвещение, 2009. — 415 с.
- Яковлев И. В. Уравнения высших порядков, https://mathus.ru/










