В данной статье рассматривается решение одной геометрической задачи разными способами. Отыскание различных способов решения задач — важнейшее средство развития творческого мышления учащихся, способствует более глубокому и прочному пониманию и запоминанию материала.
Ключевые слова: треугольник, медиана, высота, биссектриса, угол.
Лучше решить одну задачу несколькими методами, чем несколько задач — одним.
Д. Пойя
В современной педагогике преподавательская практика точных наук показывает, что для учащихся 7–9 классов обучение предмету математики, особенно геометрии, посредством предложения разных путей решения задач является одним из лучших методов (способов), который может привлечь внимание ученика, повысить его заинтересованность и стремление к решению задач. В качестве примера такого подхода приведём решение несколькими разнообразными способами следующей задачи из области геометрии.
Задача. В треугольнике АВС из вершины А проведены высота, биссектриса и медиана. Они делят угол А на четыре равные части. Доказать, что этот угол прямой.
Ниже предлагается 11 путей решения этой задачи.
Способ I. Метод равенства площадей.
1) Площадь треугольника
АВС
(рис.1) можно записать в виде:
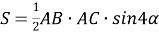
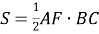
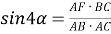
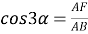
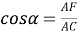
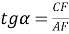
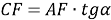
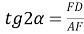
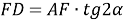
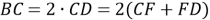
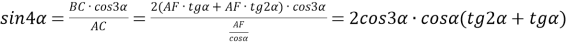
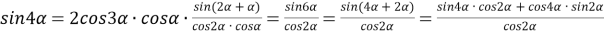
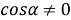
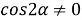
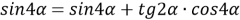
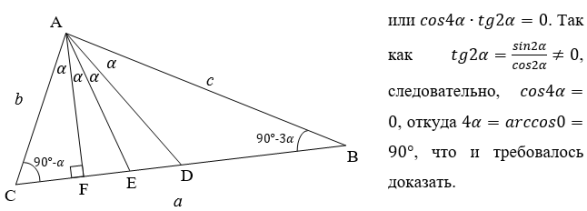
Рис. 1
Способ II. Применение теоремы Стюарта.
2) Треугольник
АВС
(рис.1) будет прямоугольным тогда, когда
AD=BD
. По теореме косинусов из треугольника
АВС
будем иметь:
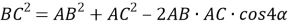
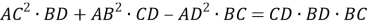
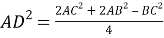
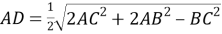
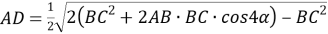
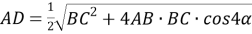
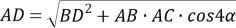
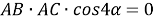
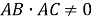
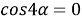
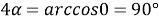
Способ III. Применение теоремы о свойстве биссектрисы внутреннего угла треугольника.
3) По свойству биссектрисы внутреннего угла треугольников
АВС
и
АВЕ
(рис.1) имеем:
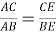
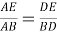
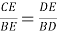
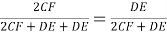
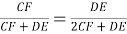
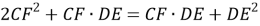
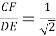
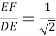
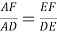
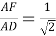
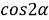
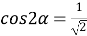
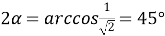
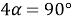
Способ IV. Метод тригонометрических функций.
4) Из прямоугольного треугольника
АFC
(рис.1) имеем:
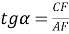
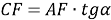
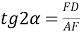
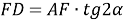
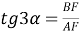
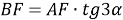
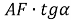
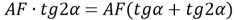
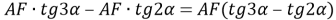
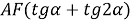
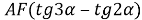
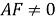
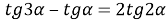
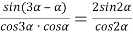
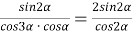
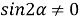
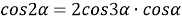
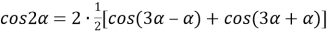
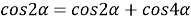
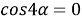
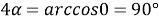
5) Из треугольника
АВС
по теореме косинусов (рис.1) имеем:
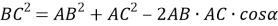
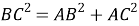
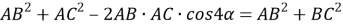
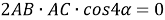
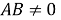
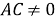
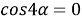
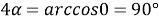
6) Из треугольника
АВD
(рис.1) по теореме синусов имеем:
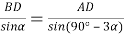
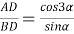
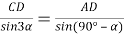
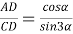
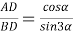
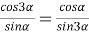
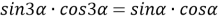
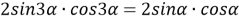
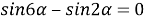
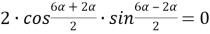
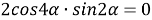
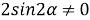
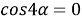
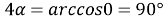
7) Из треугольника
АDС
(рис.1) по теореме косинусов имеем:
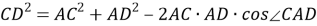
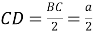
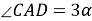
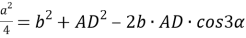
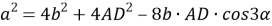
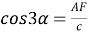
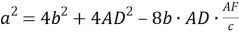
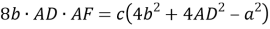
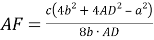
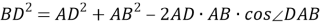
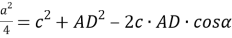
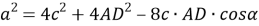
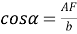
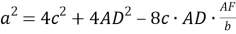
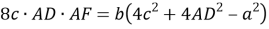
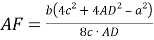
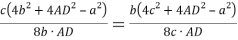
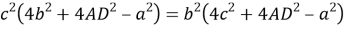
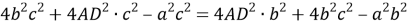
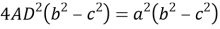
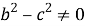
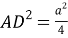
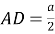
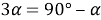
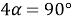
8) Из треугольника
АВC
(рис.1) по теореме синусов имеем:
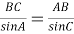
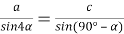
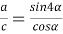
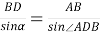
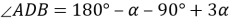
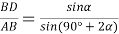
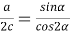
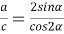
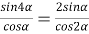
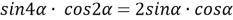
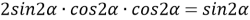
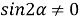
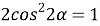
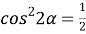
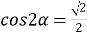
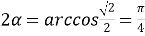
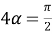
9) Из Интернета. Воспользуемся тем, что в любом треугольнике биссектриса лежит между медианой и высотой (это известный факт и легко доказывается). Итак, пусть один из этих четырёх углов равен
х
. Тогда один из углов данного треугольника равен
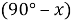
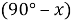
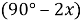
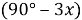
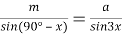
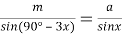
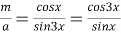
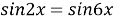
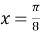
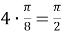
Способ V. Применение теоремы об описанном четырёхугольнике.
10) Опишем окружность около треугольника АВС (рис.2). Проведём FK ┴ AC через точку M
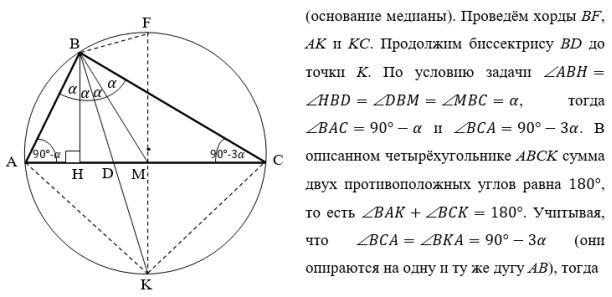
Рис. 2
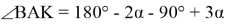
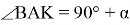
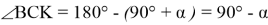
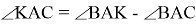
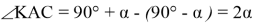
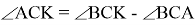
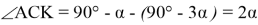
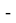
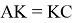
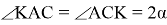
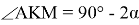
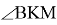
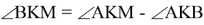
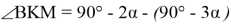
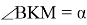
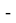
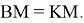
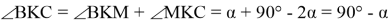
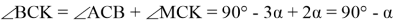
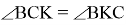
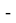
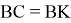
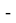
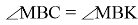
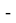
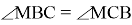
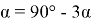
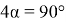
Способ VI. Подобие прямоугольных треугольников.
11) Из Интернета. Обозначим полученные углы через 𝛼 (рис.3). Итак, строим описанную окружность. Теперь продлеваем биссектрису и строим перпендикуляр к стороне AC в точке пересечения медианы. Прямоугольные треугольники BDN и MDN подобны, значит OMN = DBN =𝛼. Но тогда ΔBOM — равнобедренный и BO=OM , значит, O — центр описанной окружности около нашего треугольника и, причём точка O — середина стороны AC . Значит AC — гипотенуза и B =90º.
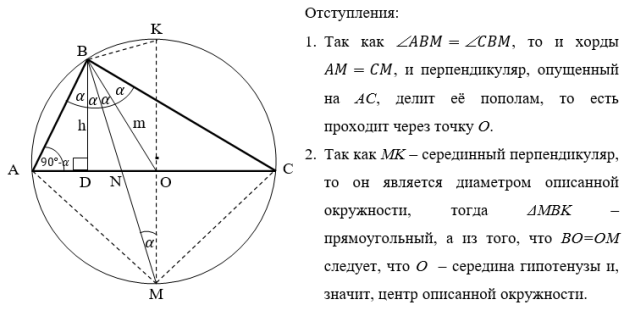
Рис. 3
В представленной работе рассмотрены различные способы решения одной геометрической задачи и, анализируя все решения, приходим к следующим важным выводам:
- Благодаря такой работе снимается психологический барьер перед поиском решения задачи. Ведь если знаешь, что задача имеет несколько способов решения, то смелее берёшься за неё. Постепенно решая задачу за задачей, приобретаешь некоторый опыт, что позволит развить математическое чутьё.
- При такой работе над задачей формируется логическое мышление.
- Подробный разбор способов решения задач является хорошим подспорьем для того, чтобы освежить в памяти пройденный материал.
- Овладевая основными методами решения задач, составляющими важную часть многих эвристических алгоритмов, можно рационально планировать поиск решения задачи, выполнять полезные преобразования условия задачи, а также использовать известные приёмы познавательной деятельности — наблюдение, сравнение, обобщение.
Все перечисленные факторы создают условия для формирования у учащихся навыков исследовательской деятельности, способствующей накоплению творческого потенциала.
Литература:
- Василевский А. Е. Методы решения математических задач. Минск, 1969.
- Литвиненко В. Н. Практикум по решению задач школьной математики (Геометрия). Выпуск IV. — М: Просвещение, 1989.
- Выгодский М. Я. Справочник по элементарной математике. Москва. «Наука». 1986.
- Некрасов В. Б. Школьная математика. Санкт-Петербург. «Авалон». 2006.










