Данная статья посвящена изучению гравитационных взаимодействий небесных тел в разных системах. В ней раскрывается возможность создания компьютерной модели для рассмотрения движения компонентов различных систем с помощью языка программирования Python.
В детстве, читая произведения Стивена Хоккинга об удивительных космических приключениях мальчика Джорджа и его друзей, я очень заинтересовалась темой изучения космического пространства и устройством суперкомпьютера Космос. Так, зародилась идея создания моего проекта. Желание узнавать новое подкреплялось постоянными научными новостями об ухудшающемся положении нашей планеты — экологических проблемах, проблемах перенаселения, недостаточности ресурсов и невозможности вечного существования нашей Солнечной системы, что привело меня к «открытию» еще одной интересной темы — поиск альтернативных планет.
Не так давно исследователи Зигфрид Эггль из Лаборатории реактивного движения НАСА и Макс Попп из Принстонского университета и Института метеорологии Общества Макса Планка показали, что планеты земного типа в системах двойной звезды могут быть пригодными для жизни, в зависимости от взаимного расположения небесных тел, их движения относительно друг друга.
В своем проекте я проводила оценку взаимодействий небесных тел с помощью метода компьютерного моделирования. Для меня было важным рассмотреть разнообразные системы тел, ведь, к сожалению, информация об этом не столь популяризирована вне узких научных кругов, что, по моему мнению, является проблемой. Для реализации своей задумки я решила разработать инструмент для расчета траекторий движения тел в гравитационном поле.
Свою исследовательскую работу я начала с изучения частного случая расположения тел — системы двойной звезды — системы двух звезд, связанных силами гравитационного взаимодействия, вращающихся вокруг единого центра масс. В своей работе я рассматривала Разделенные двойные звезды — звезды обмен масс между которыми невозможен, что дает возможность опираться на постоянство масс тел при создании математических моделей процессов.
Обращаясь к школьным знаниям, я могла физически обосновать движение тел в нашей системе — системе одной звезды. Мне было необходимо выяснить, какие з акономерности будут справедливы в других ситуациях, а также расширить свои познания для уже известного случая. Для этого я изучила основы астрофизики, а именно деятельность ученых в этом вопросе, начиная с самых начал небесной механики Птолемея и Коперника до открытий Кеплера и Ньютона. В итоге, я установила, что в различных системах взаимодействия тел также будут подчиняться законам Ньютона и Кеплера .
Переходя к моделированию, необходимо обозначить определенные ограничения . Будем считать задачу модельной, то есть существующей в идеальных условиях, таких как незначительность размеров небесных тел, постоянство масс, отсутствие сопротивления межпланетного пространства; процессы подчиняются закону тяготения Ньютона, система считается достаточно удаленной от остальных объектов, то есть учитывается только влияние входящих в систему тел.
Далее, построим математические модели процессов. Для более простого понимания, начнем со знакомой нам системы одной звезды на координатной плоскости. Расставим силы и выведем, согласно Второму закону Ньютона и Гравитационному закону Ньютона, математические взаимосвязи между характеристиками тел, затем проделаем то же для случая двойной звезды, используя метод сдвига системы координат.
Суммарное ускорение планеты, создаваемое системой двух звезд, равно сумме ускорений, создаваемых каждой из звезд в отдельности. Решим задачу о движении планеты в системе координат привязанной к звездам — звезды располагаются на оси OX на равных расстояниях от начала координат.
В системе стороннего наблюдателя это соответствует движению звезд по одной окружности.
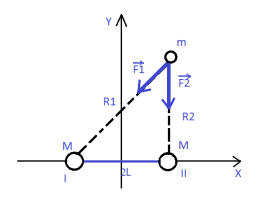
M, m — массы звезд и планеты, F1, F2 — силы притяжения
2L — расстояние между звездами
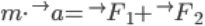
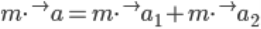
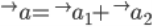
Проекции на оси:
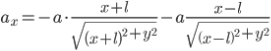
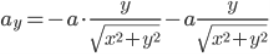
Для решения системы n-тел необходимо многократно (для каждой пары тел из системы) решить задачу о взаимодействии двух тел, общее ускорение одного тела будет равно сумме ускорений, создаваемых другими телами системы.
Дальнейшее решение полученных выражений будем проводить численными методами.
Полученную физическую модель необходимо преобразовать в компьютерную, чтобы приобрести расчетный инструмент для построения траекторий движения тел, для этого будем использовать язык программирования Python 3.
Программа состоит из нескольких блоков, отвечающих за разные задачи: расчетный блок, блок создания графического представления, блок анимации. А также снабжена различными вариантами оптимизации работы алгоритма.
Алгоритм включает в себя два варианта расчета, различных по точности. Менее точный метод подразумевает, что в течении короткого промежутка времени dt, ускорение неизменно. Это позволяет получать приближенные значения для новых координат тел.
Для повышения точности вычислений будем использовать метод Рунге-Кутты 4 порядка.
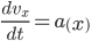
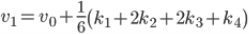
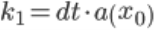
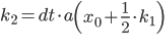
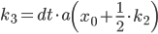
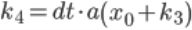
Это пример применения метода Рунге-Кутты для нахождения изменения скорости по оси ОХ. Аналогично был применен данный метод для поиска изменения скорости по оси ОУ и для изменения координат.
Для оптимизации, был реализован алгоритм динамического вычисления шага модели dt, что также положительно сказалось на точности расчетов.
Теперь необходимо подумать о графической реализации нашего алгоритма, для этого используем модуль Tkinter.
Производится рисование траектории движения по точкам и анимация движения тел, которая вызывается нажатием клавиши “a” в английской раскладке. Скорость анимации меняется с помощью клавиш “+” — увеличение и “-” — уменьшение. Результаты расчета траекторий сохраняются в файл, который можно использовать для анимации, опустив фазу вычислений, для этого создана дополнительная программа.
Немаловажным критерием полученного алгоритма является достоверность. Чтобы убедиться в соответствии данному критерию проведем проверку программы с помощью рассмотрения некоторых частных случаев, например — движение одной планеты по окружности вокруг звезды и движение симметрично заданных тел. Результаты работы программы аналогичны рассчитанным в ручную, что подтверждает достоверность полученной модели.
Представлю несколько вариантов работы написанной программы.
Пример 1. Движение планеты в системе двойной звезды (траектория в системе координат, связанной со сторонним наблюдателем)
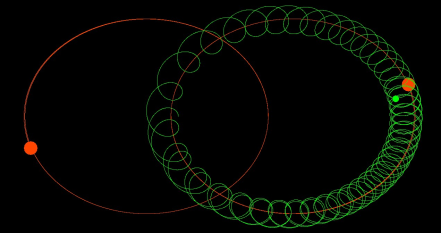
Пример 2. «Перепрыгивающая» планета. Экспериментально полученная траектория, когда планета сначала вращается вокруг одной звезды, через некоторое время захватывается гравитационным полем другой звезды и начинает вращаться вокруг другой звезды, через некоторое время возвращается к первоначальной звезде.
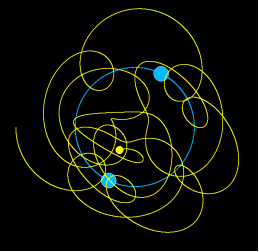
Пример 3. Анимация разрушения симметричной системы 4 тел

В процессе работы были изучены физические основы астрономии и основы программирования, рассмотрены различные варианты взаимодействия небесных тел с точки зрения физики, что позволило создать алгоритм для расчета и визуализации движения тел в различных системах.
Написанная расчетная программа удовлетворяет критерию необходимой нам точности и позволяет производить расчеты для различных систем на уроках физики, может служить интерактивным вариантом практических работ по астрономии, а также может быть использована в качестве демонстрации возможностей языка программирования Python и, в частности, графического модуля Tkinter на уроках информатики.
Наглядное представление процессов и зрелищность способствует повышению интереса к данной теме у учащихся, что является немаловажным для развития астрономических познаний.
Информация о характере движения небесного тела позволяет судить об условиях на его поверхности, что полезно для проведения исследований в таких целях, как поиск альтернативных планет или добыча полезных ископаемых.
Программа удобна в использовании — содержит краткие инструкции по применению. Также написана 2 часть программы (отдельный файл) для рисования уже рассчитанных траекторий по данным из файла, создаваемого в основной программе — это позволяет экономить время на расчеты при демонстрации.
Литература:
- Дубошин Г. Н. Небесная механика. Аналитические и качественные методы — М.: «Наука», 1978. — 456 с.
- https://www.nasa.gov/mission_pages/chandra/images/binary-stars-ejected-from-fornax-cluster.html
- https://studme.org/199301/informatika/metod_runge_kutty_chetvertogo_poryadka
- https://pythonru.com/uroki/obuchenie-python-gui-uroki-po-tkinter
- https://rosuchebnik.ru/material/velikie-otkrytiya-v-astronomii/










