Признаки делимости натуральных чисел



Актуальность : Математики прошлых веков придумали множество удобных уловок, чтобы облегчить расчеты и вычисления, которыми изобилует решение математических задач. Вполне разумный выход из положения, ведь у них не было ни калькуляторов, ни компьютеров. В некоторых ситуациях умение пользоваться удобными способами вычисления значительно облегчает решение задач и существенно сокращает затраченное на них время. К подобным полезным приемам вычисления, несомненно, относятся признаки делимости на число.

Теория делимости, по одной из версий, возникла из-за практических потребностей людей, которые возникали при строительстве уже самых примитивных сооружений, где было необходимо рассчитать, сколько примерно материала пойдет на постройку и т. п. Либо при развитии торговли, людям нужно было уметь считать товар и деньги, чтобы не быть обманутыми. В современной жизни у нас также часто возникает необходимость узнать, делится ли одно число на другое без остатка. Не всегда под рукой имеются технические средства, чтобы это быстро рассчитать. Для подсчета без калькулятора можно использовать признаки делимости: в банковском деле, при денежных расчетах в магазине и т. п.

Признак делимости — правило, позволяющее сравнительно быстро определить целочисленное деление чисел без необходимости выполнять фактическое деление.

Признаки делимости используются при решении различных математических задач, при нахождении общего знаменателя дробей, при техниках быстрого счета, в задачах ОГЭ и ЕГЭ, в задачах олимпиадного характера и в различных числовых фокусах.

Работа имеет теоретический характер и большое практическое применение. Ее можно использовать для самостоятельной подготовки для участников олимпиад и математических конкурсов.

Гипотеза: Признаки делимости — не просто математическое занудство, а полезный лайфхак в решении задач.

Объект исследования: Делимость натуральных чисел.

Предмет исследования: Признаки делимости натуральных чисел.

Решение олимпиадных задач.

Цель: Рассмотреть методы построения признаков делимости чисел.

Доказать важность и необходимость изучения этой темы для решения олимпиадных задач.

Научиться их применять в решении задач олимпиадного характера.

Задачи исследования:

— Рассмотреть основные свойства теории делимости натуральных чисел.

— Рассмотреть признак Паскаля, как универсального метода получения признаков делимости.

— Составить сводную таблицу «Признаков делимости натуральных чисел».

— Рассмотреть другие методы построения признаков делимости. Создать программу в Компасе для нахождения признаков делимости на простое натуральное число, последняя цифра которого оканчивается 1, 3, 7 и 9 по предложенным теоремам Виктора Цекунова «Просто о признаках делимости». Подобрать задачи из олимпиад различных лет, решаемых с помощью признаков делимости натуральных чисел.

— Рассмотреть практическое применение признаков делимости натуральных чисел при решении задач олимпиадного характера. Составить буклет задач для подготовки к олимпиадам по делимости натуральных чисел по материалам проведенных различных олимпиад.

Методы исследования: Сбор и изучение информации, обработка, анализ, синтез, наблюдение и сравнение данных, обобщение опыта.

Новизна представленной работы состоит в том, что это направление не рассмотрено основательно, со всей глубиной. Привлечь внимание учеников, интересующих математикой для своего математического саморазвития.

Практическая значимость материал данной исследовательской работы можно использовать для качественной подготовки к олимпиадам по теме «Признаки делимости натуральных чисел».

1. Введение

Как известно, вычитание и деление на множестве натуральных чисел выполнимо не всегда. Вопрос о существование разности натуральных чисел, а и b решается просто-достаточно установить (по записи чисел), что b < a .

Для деления натуральных чисел такого общего и простого признака нет. Поэтому в математической науке с давних пор пытались найти такие правила, которые позволили бы по записи числа а узнавать, делится ли оно на число b или нет, не выполняя непосредственно деления а на b . В результате этих поисков и были открыты признаки делимости.

Задачи на делимость натуральных чисел интересны и красивы, не зря они привлекают ученых в течении многих уже столетий. Во все времена человека поражало, что на простые вопросы о числах так трудно найти ответ...

В начале 6-го класса мы изучаем основные признаки делимости на уроках математики, но существуют еще и другие признаки делимости, которые в школе мы не изучаем. Их очень много, и многие из них в применении очень непросты, я в них запутался и поэтому решил в них разобраться.

В своей работе я постараюсь доказать, что признаки делимости — это важное и существенное понятие в математике, значительно облегчающее процесс расчетов, необходимый лайфхак для решения задач, в том числе и олимпиадных задач.

2. Основные понятия и свойства теории делимости натуральных чисел

Определение: Рассмотрим множество натуральных чисел N. Число делится на число (b≠0), если существует число , такое, что а=bс (например, 56 делится на 8, т.к. 56=8х7).

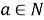
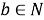
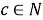
При этом используют следующую терминологию:

1. число b является делителем числа a; Делитель — это число, которое делит данное число без остатка.
2. делимое a кратно числу b. Используют специальный символ — три вертикальные точки ⁝ . Запись a ⁝b, означает, что a делится на b или что « a кратно b» .
3. число с называется частным от деления а на b.

Пример: Шесть делится нацело на 1, 2, 3 и 6. Эти числа 1236 называются делителями числа 6. Они его делят нацело, а число 6, в свою очередь, делится на них нацело и называется кратным этим числам. Число 6 кратно одному, кратно двум, кратно трём и кратно 6.

Таким образом, делимость — это способность одного числа делиться на другое без остатка.

Признак делимости — это правило, по которому, не выполняя деление, можно определить, делится ли одно натуральное число на другое (или, по-другому говоря, кратно).

Основные свойства отношения делимости:

Лемма 1. Если " " и , то .

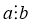
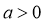
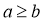
Лемма 2. Отношение делимости на множестве N является рефлексивным , антисимметричным и транзитивным .

а) рефлексивность . Действительно, любое число делится само на себя , т. к. существует число 1, для которого имеет место равенство

.

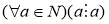
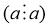
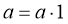
б) антисимметричность

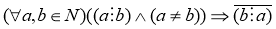
в) транзитивность :

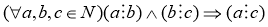
Свойства делимости:

Если a>0 и a⁝b, то a≥b

Если a⁝b и b⁝c, то a⁝c

Если a⁝c и b⁝c, то (a+b)⁝c

Если a⁝(bc), то a⁝b, a⁝c и (a:b)⁝c

Если a⁝b и b⁝а, то a=b

Если a⁝b, k€N,то ak⁝bk

Если a⁝c и b⁝c, m€N, n€N, то (am+bn)⁝c

Если a⁝c и (a+b)⁝c, то b⁝c

3. Универсальный признак делимости Паскаля

Большой вклад в изучение признаков делимости чисел внес Блез Паскаль . Он родился в 1623 году. Один из самых знаменитых людей в истории человечества. Паскаль прожил короткую жизнь 39 лет, но, несмотря на это, вошел в историю как выдающийся математик, физик, философ и писатель. Его именем названы единица давления (паскаль) и весьма популярный язык программирования. Но научные интересы Б.Паскаля не ограничивались созданием калькулятора: он нашел общий алгоритм для нахождения признаков делимости любого целого числа на любое другое целое число.

Признак Паскаля — это метод, позволяющий получить признаки делимости на любое число. Приступим к его описанию на примере натуральных чисел и десятичной системы счисления.

Признак Паскаля:

Натуральное число, A разделится на другое натуральное число m только в том случае, если сумма произведений цифр числа, A на соответствующие остатки, получаемые при делении разрядных единиц на число m , делится на это число.

Признак Паскаля — метод, позволяющий получить признаки делимости на любое число. Своего рода «универсальный признак делимости». Хотя такой способ построения признаков делимости и громоздкий и требует больших математических расчетов.

4. Методы построения признаков делимости

1. Классификация признаков делимости натуральных чисел

Признаки делимости натуральных чисел должны соответствовать следующим условиям:

Во-первых, по любому числу m он должен действительно давать признак делимости на это число. Он должен сказать, как «перерабатывать» каждое натуральное число m в соответствующий признак. Именно в этом состоит его результативность .

Во-вторых, общий признак должен быть определенным , т. е., примененный к заданному числу m , он должен приводить вполне определенным способом к вполне определенному признаку делимости на это число.

В-третьих, признак должен быть массовым , т. е., действительно общим, и давать признаки делимости на любое наперед заданное натуральное число.

Знание и использование признаков делимости натуральных чисел значительно упрощает многие вычисления, этим самым, экономя время; исключая вычислительные ошибки, которые можно сделать при выполнении действия деления.

Решение вопроса о делимости чисел признаки делимости сводят к действиям над небольшими числами, обычно выполняемым в уме.

Существует несколько классификаций признаков делимости, я ниже представляю одну из них:

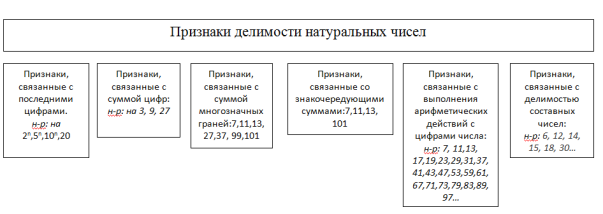
а) Признаки, связанные с последними цифрами

Сюда относятся признаки делимости на 2 ⁿ , 5 ⁿ , 10 ⁿ . Известно, что 2 ¹ =2; 2 ³ =8; 5 ¹ =5; 10 ¹ =10 …а это уже известные нам признаки делимости.

Признак делимости на 2 ⁿ : Число делится на 2 ⁿ (n — натуральное число) тогда и только тогда, когда n последних цифр этого числа образуют число, которое делится на 2 ⁿ (n>0).

Пример: 67832000делится на 32, так как 32=2 ⁶ , а 32000 делится на 32.

Признак делимости на 5 ⁿ : Число делится на n-ю степень пятёрки тогда и только тогда, когда число, образованное его последними n цифрами, делится на ту же степень (n>0).

Пример:461 125 делится на 125, так как 125=5 ³ , а 125 делится на 125.

Признак делимости на 10 ⁿ : Числоделится на n-ю степень тогда и только тогда, когда число n его последних цифр — нули, т. е. число делится на 100, если оно оканчивается двумя нулями.

б) Признаки, связанные с суммой цифр

Что такое цифровой корень числа? Найдём сумму его цифр. У результата также найдём сумму цифр, и так до тех пор, пока не получится однозначное число. Полученный результат называется цифровым корнем числа. К примеру, цифровой корень числа 654321 равен 3: 6+5+4+3+2+1=21,2+1=3. Это понятие используется в признаках делимости на 3, 9.

в) Признаки, связанные с суммами многозначных граней

Грани числа — это числа, получаемые разбиением исходного числа на двузначные или трёхзначные числа, взятые справа налево. Например, разбиение числа 1234567 на двузначные грани выглядит так: 1|23|45|67, а на трёхзначные так: 1|234|567.

Двузначные грани числа — это числа, которые получены разбиением исходного числа на двузначные числа. Например, разбиение числа 123456789 на двузначные грани выглядит так: 1|23|45|67|89 (разбиение числа начинается с его конца). Числа 1, 23, 45, 67, 89 являются двузначными гранями числа 123456789.

Трёхзначные грани числа — это числа, полученные разбиением исходного числа на трёхзначные числа. Например, разбиение числа 1234567890 на трёхзначные грани выглядит так: 1|234|567|890. Числа 1, 234, 567, 890 являются трёхзначными гранями числа 1234567890.

г) Признаки, связанные со знакочередующими суммами

Термин «знакочередующаяся сумма» означает, что первое слагаемое суммы берётся со знаком «плюс», второе — со знаком «минус», третье — опять со знаком «плюс» и т. д. То есть знаки перед слагаемыми чередуются.

Например , двузначные грани числа 1234567 — это 1, 23, 45, 67. Их знакочередующаяся сумма равна 1 ‐ 23 + 45 ‐ 67 = ‐44.

д) Признаки, связанные с выполнением арифметических действий с цифрами числа

Считается одной из самой трудной группы признаков делимости натуральных чисел. Легко заметить, что группы в, г и д связаны последней цифрой, она либо 1, либо 3, либо 7 или 9. Мне стало интересно, нет ли какого-нибудь общего признака для них. Ответ свой я представил чуть ниже.

е) Признаки, связанные с делимостью составных чисел

Эти признаки, основанные на следующей теореме:

Теорема (общий признак делимости на составное число): Для того чтобы натуральное число х делилось на составное число n=bc , где числа b и c таковы, что НОД( b,c ) = 1, необходимо и достаточно, чтобы оно делилось на b и на c .

Таким образом, чтобы узнать, делится ли заданное число на составное, нужно разложить это составное число на взаимно простые множители . Например, число делится нацело на 18, если оно делится нацело на 2 и 9, и применить признаки делимости и на 2 и на 9 одновременно. В данном случае нельзя раскладывать 18 на 3 и 6, поскольку они не являются взаимно простыми, так как имеют общий делитель 3.

Поэтому признаки делимости на 14, 15, 18, 20, 21, 24, 26, 28 и прочие составные числа проверяем делимость на взаимно-простые множители этих чисел:

Для 14: на 2 и на 7;

Для 15: на 3 и на 5;

Для 18: на 2 и на 9;

Для 21: на 3 и на 7;

Для 20: на 4 и на 5;

Для 24: на 3 и на 8;

Для 26: на 2 и на 13;

Для 28: на 4 и на 7;

Для 1007: на 7 и на 11 и на 13;

………………

Заметим, что выше данную теорему можно применять многократно. Рассмотрим, например, признак делимости на 60 . Для того, чтобы число делилось на 60, необходимо и достаточно, чтобы оно делилось на 4 и на 15. Но в свою очередь, число делится на 15 тогда и только тогда, когда оно делится на 3 и на 5. Поэтому признак делимости на 60 может быть сформулирован иначе: для того, чтобы число делилось на 60, необходимо и достаточно, чтобы оно делилось на 4, на 3, на 5.

После классификации я представляю сводную таблицу всех рассмотренных мною признаков делимости натуральных чисел:

Сводная таблица всех признаков делимости натуральных чисел

Признак делимости	Правило
На 2	Число делится на 2 тогда и только тогда, когда его последняя цифра делится на 2, то есть является чётной: 0, 2, 4, 6 или 8; 87654 ⁝2, так как последняя цифра 4.
На 3	Число делится на 3 тогда и только тогда, когда сумма его всех цифр (цифровой корень числа) делится на 3. 345 ⁝3, так как 3+4+5=12 делится на 3.
На 4	1-й признак: Делимость на 4 зависит от двух последних цифр в записи числа. Число делится на 4 только тогда, когда две его последние цифры — нули или составляют число, которое делится на 4. 3200 ⁝4, так как 0 делится на 4. 2-й признак: Натуральное число делится без остатка на 4, если сумма предпоследней цифры в его записи и половины последней цифры — чётное число. Схематически делимость на 4 трёхзначного числа в этом случае выглядит так: abc делится на 4, если b+c:2 –четное число. Для шестизначного числа признак делимости на 4 схематично можно изобразить так: а bcdef делится на 4, если e + f :2 – четное число. 234 52 ⁝4, так как 52 делится без остатка на 4 (5+2:2=5+1=6 — чётное число); 837 60 ⁝ на 4, так как 60 делится на 4 (6+0:2=6 — чётное число).
На 5	Число делится на 5 тогда и только тогда, когда последняя цифра делится на 5, т. е. если она 0 или 5. 4560 ⁝5, так как оканчивается на 0.
На 6	Число делится на 6 тогда, когда оно делится и на 2, и на 3 (то есть если оно четное и сумма его цифр делится на 3).
На 7	Признак делимости на 7 часто пропускается из-за сложности его вычислений. 1-й признак. Число делится на 7 тогда и только тогда, когда знакочередующаяся сумма трехзначных граней числа делится на 7. 138689257 ⁝7 так как, 138–689+257=294, а 294 делится на 7. 2-й признак. Число делится на 7 тогда и только тогда, когда результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на 7. 357 ⁝7, так как 35–2·7=21 делится на 7. Схематично признак делимости на 7 трёхзначного числа можно изобразить так: abc делится на 7, если ab -2 c делится на 7. Для шестизначного числа делимость на 7 схематично выглядит так: а bcdef делится на 4, если abcde-2 f делится на 7. 574: 57–2∙4=57–8=49. 49 делится на 7, значит, 574 также делится на 7. 3-й признак. Число делится на 7 тогда и только тогда, когда разность числа десятков и удвоенного числа единиц, взятая по модулю, делится на 7. 364 делится на 7, так как 36–4·2=28, а 28 делится на 7.
На 8	Число делится на 8 тогда и только тогда, когда число, образованное тремя его последними цифрами, делится на 8. В остальных случаях — не делится. 32800 ⁝8, так как 800 делится на 8. Можно указать подобные признаки и для деления на 16, 32, 64 и т. д., но они не имеют практического значения.
На 9	Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9. 345 не делится на 9, так как 3+4+5=12 не делится на 9.
На 10	Число делится на 10 тогда и только тогда, когда оно оканчивается на нуль. 4560 ⁝10, так как оканчивается на 0.
На 11	Всего существует три важных признака делимости на 11. 1-й признак: Число делится на 11, если знакочередующаяся сумма его цифр делится на 11. Этот признак является наиболее простым и удобным. К тому же его проще всего запомнить. 1234321⁝11. т. к. Знакочередующаяся сумма цифр этого числа равна 1 − 2 + 3 − 4 + 3 − 2 + 1 = 0. т. к. 0 делится на 11, то и число 1234321 делится на 11. Если не верите — возьмите калькулятор и проверьте! Вообще говоря, многие красивые числа делятся на 11. 2-й признак: Число делится на 11, если сумма его двузначных граней делится на 11 . 1002001⁝11 т. к. сумма двузначных граней числа 1002001 равна 1 + 20 + 0 + 1 = 22. Число 22 делится на 11. 3-й признак: число делится на 11, если знакочередующаяся сумма его трёхзначных граней делится на 11. Разбиваем число 1002001 на трёхзначные грани: 1|002|001. Их знакочередующаяся сумма равна 1 − 2 + 1 = 0 — делится на 11. Поэтому 1002001 делится на 11.
На 12	Признак делимости на 12 — это объединение признаков на 3 и на 4.
На 13	1-й признак. Число делится на 13 тогда и только тогда, когда на 13 делится знакочередующаяся сумма трехзначных граней. 132639 делится на 13, так как 132–639=-507 делится на13. 2-й признак. Число делится на 13 тогда и только тогда, когда сумма десятков и единиц, увеличенных в 4 раза кратна 13. 234 делится на 13, так как 23+4·4=39 делится на 13;
На 14	Признак делимости на 14 — это объединение признаков на 2 и на 7.
На 15	Признак делимости на 15 — это объединение признаков на 3 и на 5.
На 16	1-й признак. Делимость натурального числа на 16 зависит от четырёх последних цифр в его записи. Натуральное число делится без остатка на 16: если последние четыре цифры в его записи образуют число, которое делится на 16 или если его запись оканчивается четырьмя нулями . 2-й признак. Натуральное число делится на 16 без остатка, если сумма — цифра из разряда тысяч, умноженная на 8, плюс цифра из разряда сотен, умноженная на 4, плюс цифра из разряда десятков, умноженная на 10, плюс цифра из разряда единиц, — делится на 16. Схематически второй признак делимости на 16 для четырехзначного числа можно изобразить так: а bcd делится на 16, если 8 a +4 b +10 c + d - делится на 16. Для шестизначного числа делимость на 16 схематически выглядит так: а bcdef делится на 16, если 8 c +4 d +10 e + f - делится на 16. 1072:16 т. к. 8∙1+4∙0+10∙7+2=8+0+70+2=80. Так как 80 делится на 16, то и 1072 делится на 16 нацело.
На 17	Делимость числа на 17 зависит от соотношения между цифрами числа без его последней цифры и этой последней цифрой. Натуральное число делится на 17, если разность — это число без его последней цифры минус его последняя цифра, умноженная на 5, — делится на 17. Для трёхзначного числа признак делимости на 17 схематично можно изобразить так: а bc делится на 17, если ab -5 c - делится на 17. Для шестизначного числа делимость на 17 выглядит так: а bcdef делится на 17, если abcde -5 f - делится на 17.
На 18	Признак делимости на 18 — это объединение признаков на 2 и на 9.
На 19	Делимость на 19 зависит от соотношения цифр в записи числа с его последней цифрой. Натуральное число делится на 19, если сумма — это число без его последней цифры плюс удвоенная последняя цифра — делится на 19. 646 ⁝19, так как на 19 делятся 64+2*6=76{\displaystyle 64+2\cdot 6=76} и 7+2*6=19 Схематично признак делимости на 19 трёхзначного числа можно изобразить так: а bc делится на 19, если ab +2 c - делится на 19. Для шестизначного числа делимость на 19 схематично выглядит так: а bcdef делится на 17, если abcde +2 f - делится на 19.{\displaystyle 7+2\cdot 6=19.}
На 20	1-й признак. Число делится на 20 тогда и только тогда, когда число, образованное двумя последними цифрами, делится на 20. 2-й признак. Признак делимости на 20-это объединение признаков на 4 и на 5.
На 21	Признак делимости на 21 — это объединение признаков на 3 и на 7.
На 23	1-й признак. Натуральное число делится на 23, если сумма — это число без его последней цифры плюс последняя цифра, умноженная на 7, — делится на 23. Схематически делимость на 23 трёхзначного числа можно изобразить так: а bc делится на 23, если ab +7 c - делится на 23. Признак делимости на 23 шестизначного числа схематично выглядит так: а bcdef делится на 17, если abcde +7 f - делится на 23. 3082⁝23 так как 308+7∙2=308+14=322, 32+7∙2=32+14=46. Так как 46 делится на 23, то и 3082 делится на 23.
На 24	Признак делимости на 24 — это объединение признаков на 3 и на 8.
На 25	Число делится на 25 тогда и только тогда, когда две его последние цифры составляют число, которое делится на 25. Существует всего только 4двуциферных окончания для числа, делящегося на 25. Это 00, 25.50 и 75.
На 26	Число делится на 26 тогда и только тогда, когда оно делится на 2 и на 13.
На 27	Число делится на 27 тогда и только тогда, когда на 27 делится сумма чисел, образующих группы по три цифры (начиная с единиц). 142857⁝27 т.к 142+857=999 а 999⁝27.
На 28	Число делится на 28 тогда и только тогда, когда оно делится на 4 и на 7.
На 29	Число делится на 29 тогда и только тогда, когда число десятков, сложенное с утроенной цифрой в разряде единиц, делится на 29. 261 ⁝ 29, так как {\displaystyle 26+3\cdot 1=29}26+3*1=29 делится на 29.
На 30	Число делится на 30 тогда и только тогда, когда оно делится на 3 и на 10.
На 31	Число делится на 31 тогда и только тогда, когда модуль разности числа десятков и утроенного числа единиц делится на 31. 7998 ⁝31, так как |799–3*8| = |799–24| = 775, |77–3*5| = |77–15| = 62 ⁝31.
На 34	Число делится на 34 тогда и только тогда, когда оно делится на 2 и на 17.
На 35	Число делится на 35 тогда и только тогда, когда оно делится на 5 и на 7.
На 36	Число делится на 36 тогда и только тогда, когда оно делится на 4 и на 9.
На 37	1-й признак Число делится на 37 тогда и только тогда, когда при разбивании числа на группы по три цифры (начиная с единиц) сумма этих групп кратна 37. 2-й признак Число делится на 37 тогда и только тогда, когда на 37 делится модуль утроенного числа сотен, сложенного с учетверённым числом десятков, за вычетом числа единиц, умноженного на семь. 851 ⁝ 37, т. к. делится |3*8 + 4*5–1*7| = |24 + 20–7| = |44–7| = 37 ⁝37. 3-й признак Число делится на 37 тогда и только тогда, когда на 37 делится модуль суммы числа сотен с числом единиц, умноженного на десять, за вычетом числа десятков, умноженного на 11. 592 ⁝37, т. к. |5–11*9 + 10*2| = |5–99 + 20| = |- 74| = 74 делится на 37. Необычное число 37: Любое число, состоящее из 3-х одинаковых цифр, делится на 37. Н-р: числа 111, 222, 333 и все остальные, кратные 111 — делятся на 37. Также, шестизначное число делится на 37, если при разложении его на две группы (по 3 цифры) сумма чисел этих групп делится на 37, либо составляет число из трех одинаковых цифр. Н-р: 259185 ⁝37, так как 259 + 185 = 444.
На 38	Число делится на 38 тогда и только тогда, когда оно делится на 2 и на 19.
На 39	Число делится на 39 тогда и только тогда, когда оно делится на 3 и на 13.
На 40	Число делится на 40 тогда и только тогда, когда оно делится на 5 и на 8.
На 41	1-й признак. Число делится на 41 тогда и только тогда, когда модуль разности числа десятков и четырёхкратного числа единиц делится на 41. 533 ⁝41, т. к. |53–4*3| = |53–12| = 41. 2-й признак. Чтобы проверить, делится ли число на 41, его следует справа налево разбить на грани по 5 цифр в каждой. Затем в каждой грани первую справа цифру умножить на 1, вторую цифру умножить на 10, третью — на 18, четвёртую — на 16, пятую — на 37 и все полученные произведения сложить. Если результат будет делиться на 41, тогда и только тогда само число будет делиться на 41.
На 42	Число делится на 42 тогда и только тогда, когда оно делится на 6 и на 7.
На 44	Число делится на 44 тогда и только тогда, когда оно делится на 4 и на 11.
На 45	Число делится на 45 тогда и только тогда, когда оно делится на 5 и на 9.
На 50	Число делится на 50 тогда и только тогда, когда число, образованное двумя его младшими десятичными цифрами, делится на 50.
На 59	Число делится на 59 тогда и только тогда, когда число десятков, сложенное с числом единиц, умноженное на 6, делится на 59. 885 делится на 59, так как 88 + 6*5 = 88 + 30 = 118, 11 + 6*8 = 11 + 48 = 59.
На 79	Число делится на 79 тогда и только тогда, когда число десятков, сложенное с числом единиц, умноженное на 8, делится на 79.
На 99	Число делится на 99 тогда и только тогда, когда на 99 делится сумма двухзначных граней. 12573 делится на 99, так как на 99 делится {\displaystyle 1+25+73=99.}1+25+73=93
На 100	Число делится на 100, если две его последние цифры — нули.
На 101	Число делится на 101 тогда и только тогда, когда знакочередующаяся сумма двухзначных граней делится на 101. 590547⁝101, т. к. 59–05+47=101 делится на 101.
На 1001	Единство признаков на 7, 11 и 13 происходит от особенностей разложения на простые множители у числа 1001=7*11*13
На 1091	Число делится на 1091 тогда и только тогда, когда разность числа десятков и умноженной на 109 цифры в разряде единиц делится на 1091. 19638 ⁝1091, т. к. 1963–8 * 109 = 1091 делится на 1091.

2. Признаки делимости на простые натуральные числа, последняя цифра которых 1, 3, 7 или 9

В изучении этой темы я нашел очень интересную математическую разработку математика Виктора Цекунова «Просто о признаках делимости» за 2011 г. Автор предлагает рассмотреть числа 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, …, 89, 97. Это простые двухзначные числа P, последняя цифра которых 1, 3, 7 или 9, и находит для них признаки делимости. Для этого он в качестве входных данных берет:

Пусть N — исходное натуральное число,

X — число N без последней цифры (x — натуральное число),

Y– последняя цифра числа N (y = 0,1,2,3,4,5,6,7,8,9),

P — простое двухзначное число;

тогда: N = 10 X + Y .

Например: число N = 389. Зачеркнём последнюю цифру 9, получим число 38.

Тогда X = 38, Y = 9 и 389 = 10·38 + 9.

Получил компактные теоремы, с помощью которых можно легко установить делимость любого натурального числа на простое число, которое оканчивается цифрой: 1,3,7 и 9.Апростых чисел много-много… бесконечно много!

ТЕОРЕМА 1 (для P = 11, 31, 41, 61, 71, …): Пусть P — простое число с цифрой 1 на конце (т. е. P = 10n+1), n — число десятков числа P, N = 10X + Y. Тогда если (X — nY) делится на P, то и N делится на P.

Пример: P = 101. Число десятков у числа 101 равно 10 (n = 10). По теореме 1 если X — nY = X — 10Y делится на 101, то и само число делится на 101. Пусть N = 2727. Имеем X = 272, Y = 7 и X — 10Y = 272–10·7 = 272–70 = 202 делится на 101. Значит и 2727 делится на 101. Действительно, 2727:101 = 27. Получили признак делимости на 101.

Пример: P = 1091. Число десятков у числа 1091 равно 109 (n = 109). По теореме 1 если X — nY = X — 109Y делится на 101, то и само число делится на 101. Пусть N = 19638. Имеем X = 1963, Y = 8 и X — 10Y = 1963–109·8 = 1963–872 = 1091 делится на 1091. Значит и 19638 делится на 1091. Действительно, 19638:1091 = 18. Получили признак делимости на 1091.

ТЕОРЕМА 2 (для P = 3, 13, 23, 43, 53, 73, 83, …): Пусть P — простое число с цифрой 3 на конце (т. е. P = 10n+3), n — число десятков числа P, N = 10X + Y. Тогда если (X + (3n+1) Y) делится на P, то и N делится на P.

Пример 1: P = 103. Число десятков у числа 103 равно 10 (n = 10). По теореме 2 если X + (3n+1) Y = X + (3·10+1) Y = X + 31Y делится на 103, то и само число делится на 103. Пусть N = 1545. Имеем X = 154, Y = 5 и X +31Y = 154 + 31·5 = 154 + 155 = 309 делится на 103. Значит и 1545 делится на 103. Действительно, 1545:103 = 15. Получили признак делимости на 103.

Пример 2: P = 3. Если (Х + Y) делится на 3, то и само число делится на 3. Пусть N = 297. Имеем X = 29, Y = 7 и X + Y = 29 + 7 = 36 делится на 3. Значит и 297 делится на 3. Действительно, 297:3 = 99. Получили признак делимости на 3.

ТЕОРЕМА 3 (для P = 7, 17, 37, 47, 67, 97, …): Пусть P — простое число с цифрой 7 на конце (т. е. P = 10n+7), n — число десятков числа P, N = 10X + Y. Тогда если (X — (3n+2) Y) делится на P, то и N делится на P.

Пример 1 : P = 107. Число десятков у числа 107 равно 10 (n = 10). По теореме 3 если X — (3n+2) Y =X — (3·10+2) Y = X — 32Y делится на 107, то и само число делится на 107. Пусть N = 315115. Имеем X = 31511, Y = 5 и X -32Y = 31511–32·5 = 31511–160 = 31351. Теперь N₁ = 31351. Имеем X₁ = 3135, Y₁ = 1 и X₁ -32Y₁ = 3135–32·1 = 3135–32 = 3103. Теперь N₂ = 3103. Имеем X₂ = 310, Y₂ = 3 и X₂ -32Y₂ = 310–32·3 = 310–96 = 214 делится на 107. Значит и 315115 делится на 107. Действительно, 315115:107 = 2945. Получили признак делимости на 107.

Пример 2: P = 7. Если (x — 2y) делится на 7, то и само число делится на 7. Пусть N = 301. Имеем x = 30, y = 1 и x — 2y = 30–2·1 = 28 делится на 7. Значит и 301 делится на 7. Действительно, 301:7 = 43. Получили признак делимости на 7.

ТЕОРЕМА 4 (для P = 19, 29, 59, 79, 89, …): Пусть P — простое число с цифрой 9 на конце (т. е. P = 10n+9), n — число десятков числа P, N = 10X + Y. Тогда если (X + (n+1) Y) делится на P, то и N делится на P.

Таким образом, из этих теорем можно получить признак делимости любого натурального числа на простое число, последняя цифра которого оканчивается на 1, 3, 7 и 9. Вот такие интересные лайфхаки я почерпнул у Виктора Цекунова «Просто о признаках делимости».

Если сравнить с признаки из cводной таблицы всех признаков делимости натуральных чисел, представленной выше, то этими теоремами порой пользоваться проще. Теперь мне благодаря этим лайфхакам все признаки кажутся несложными.

В качестве проверки этих признаков я создал программу на языке программирования Питон для признаков делимости по предложенным теоремам В. Цекунова. Ниже представляю небольшой фрагмент из этой программы:

import time

print(«Введите число P, которое оканчивается на 3")

time.sleep(1)

try:

P = int(input(«Введите: "))

except ValueError:

print(«Вы ошиблись.Это не число»)

time.sleep(0.5)

quit()

okonchanie = P % 10

if okonchanie!= 3:

print(«Число не оканчивается на 3")

quit()

time.sleep(1)

print(«Введите число N«)

try:

N = int(input(«Введите: "))

except ValueError:

print(«Вы ошиблись.Это не число»)

time.sleep(0.5)

quit()

time.sleep(1)

print(«Вычисляется формула (X+(3n+1)Y)")

time.sleep(3)

X = N//10

print(«X-число десятков N,равно»,X)

time.sleep(3)

Y = N % 10

print(«Y-число десятков n,равно»,Y)

time.sleep(3)

n = P//10

print(«n-число десятков числа P,равно»,n)

time.sleep(3)

A = (X+(3*n+1)*Y)

print(«Значение выражения (X+(3n+1)Y) =",A)

time.sleep(3)

…………………

3. Метод построения признаков делимости по малой теореме Ферма

Больше всего французского математика Пьера Ферма прославили его работы по теории чисел. Именно с работ Ферма началась новая математическая наука-теория чисел. «Меня озарило ярким светом» — писал Ферма, впервые сообщив о своем открытии в письме (1640 г). Пьер де Ферма сформулировал теорему в 1640 году, однако сам ее не доказал. Позднее это сделал Готфрид Вильгельм Лейбниц — немецкий философ, логик, математик и т. д. Эта теорема стала одним из фундаментальных фактов в теории делимости натуральных чисел. Теорема называется малой во избежание путаницы с Великой теоремой Ферма. Чаще всего эту теорему применяют в признаках делимости не в поле натуральных чисел, а в поле рациональных чисел.

Теорема: если p — простое число, а — целое число, то – а кратно р .

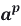
Например: a =5, p =3, тогда 5 ^3– 5=120, 120⁝3

a =8, p =5, тогда 8 ^5– 8=32760, 32760⁝5.

Следствие. Если р — простое и а не делится на р , то а ^р-1– 1 делится на р .

Например: a = 2; p = 5 ap-1–1 = 25–1–1 = 24–1 = 16–1 = 15 тогда число 15 делится на 5 без остатка.

5. Заключение

Увидев очень высокого человека, мы можем предположить, что он баскетболист. Глядя на очень большой камень, мы поймем, что нам не удастся его поднять, он слишком тяжелый. Глядя на число 252, мы понимаем, что оно делится на 2.

Во всех этих примерах мы не проверяли, а делали вывод на основе внешних признаков. Причем в первых двух случаях мы могли ошибиться, но про число 252 мы знаем точно. Последняя цифра делится на 2, значит, и все число делится. А все потому что мы применили признак делимости на 2.

Поэтому значимость признаков делимости натуральных чисел бесспорна. Ведь именно с помощью признаков делимости можно узнать, делится ли одно число на другое без остатка, не производя фактического деления. И я уверенно заключаю, что «Признаки делимости натуральных чисел» просто необходимые математические лайфхак и !!!

Познакомившись с признаками делимости чисел, я считаю, что полученные знания буду использовать в своей учебе, использовать при решении олимпиадных задач, применить изученные признаки в реальной жизненной ситуации. Работа имеет практическое применение т. к. в результате изучения темы составлен сборник задач, который будет полезным подготовки к олимпиадам. А именно, результатом моей проектной деятельности стал разработанный мной буклет «Признаки делимости натуральных чисел для подготовки к олимпиадам». Я постарался изложить материал по признакам делимости доступным языком, чтобы каждый ученик, которому это интересно, мог взять разработанный мной буклет и самостоятельно разобрать задачи и качественно подготовиться.

В дальнейшем предполагаю продолжить работу над изучением признаков делимости чисел уже в поле рациональных чисел и дополню свой буклет уже новыми задачами.

Литература:

1. Энциклопедический словарь юного математика.
2. https://www.timetoast.com/timelines/-edfdef39-d1b4–4648–837e-2737fb631943.
3. https://www.sites.google.com/site/viktortsekunov/popularly/delimost
4. https://novstudent.ru/priznaki-delimosti/
5. https://www.sites.google.com/site/viktortsekunov/popularly/delimost.