В статье проводится анализ результатов реализации некооперативной игры «Гарвард» в МОУ СОШ № 75 им. И. М. Халатникова г. Черноголовка Московской обл. Группе игроков — обучающихся 6–11 классов предлагалось выбрать целое неотрицательное число от 1 до 100. Победителем считался тот, чье число окажется ближе чисел других игроков к половине среднего арифметического чисел, записанных всеми игроками. Игра «Гарвард» была использована как средство оценки развития аналитического и стратегического мышления школьников.
Ключевые слова: теория игр, игра Гарвард, среднее арифметическое.
Настоящая работа лежит на стыке двух математических дисциплин: теории игр и статистики. Теория игр — раздел прикладной математики, в котором разрабатываются инструменты для анализа различных ситуаций (экономических, политических, военных и т. д.), в которых стороны, называемые игроками, принимают взаимозависимые решения, называемые стратегиями [1]. В теории игр известны множество различных игр, моделирующих различные экономические, финансовые, политические, военные и другие ситуации: «Битва полов», «Диктатор», «Орлянка», «Ультиматум» и др. [2]. Одной из таких игр является игра «Гарвард» [3]. Игра «Гарвард» была предложена в одноименном университете, в качестве средства оценки развития аналитического мышления. Дизайн игры «Гарвард» следующий: группе игроков (в нашем случае, обучающихся МОУ СОШ № 75 им. И. М. Халатникова г. Черноголовка Московской обл.) предлагается выбрать и записать на листе бумаги одно из первых ста натуральных чисел, т. е. целое неотрицательное число от 1 до 100. При этом для победы в игре число должно быть выбрано не случайно. Победителем считается тот, чье число окажется ближе чисел других игроков к половине среднего арифметического ā /2 чисел a 1 , a 2 , …, a n , записанных всеми n игроками (см. формулу ниже).

Таким образом, каждый игрок должен взвесить возможные варианты, которые могут написать его соперники, оценить среднее, затем половину среднего и выбрать число, которое, по его мнению, наиболее близко к этой половине среднего.
Какой рациональной стратегии следует придерживаться в игре «Гарвард»? Для ответа на этот вопрос нужно выяснить, какое максимальное значение половины среднего арифметического можно получить? Допустим, что все пишут 100, тогда среднее пополам будет равно 50 (см. формулу ниже).
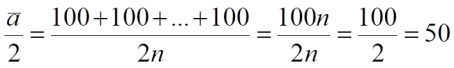
Это означает, что записывать число, превосходящее 50, не разумно, при условии, что все игроки это понимают. Т. е. в распоряжении игрока остается набор чисел от 1 до 50. В этом случае максимально возможное значение половины среднего ā /2 составляет 25. Это означает, что записывать число, превосходящее 25, также не разумно, при условии, что все игроки это понимают. Т. е. в распоряжении игрока остается набор чисел от 1 до 25. Проделав несколько итераций, можно прийти к выводу, что идеальная стратегия в игре для всех игроков — записать 1, которая окажется одинакова близка к 1/2. Следует обратить внимание на то, что существенная часть алгоритма — предположение о рациональности всех игроков. Единицу напишут те, кто считает других игроков исключительно талантливыми (способными к аналитическому мышлению). Таким образом, чем меньше значение половины среднего ā /2, тем выше уровень аналитического мышления и математического интеллекта в группе играющих.
Из литературы известны результаты игры «Гарвард», проводимой среди студентов различных вузов [3]. Было установлено, что чем престижнее вуз и сильнее в нем математическая подготовка, тем лучше результат игры. Так, например, в Независимом московском университете (узкоспециализированном математическом вузе) половина среднего ā /2 оказалась рекордно низкой — 4 [3], то есть очень большая группа людей мыслили согласно рассмотренной выше стратегии, а доля тех, кто не понял правил, свелась к минимуму. В Гарвардском университете половина среднего — 7 [3]. Это значение считается своеобразным эталоном и довольно высоким показателем уровня стратегического мышления. В Российском университете транспорта ā /2 = 18 [3]. В Белорусском государственном техническом университете ā /2 = 27 [3]. Таким образом, согласно исследованиям, в наиболее интеллектуальных коллективах значение ā /2 находится в интервале 4–10.
Игра «Гарвард» и подобные ей игры «Угадай 2/3 среднего» и «Кейнсианский конкурс красоты» достаточно хорошо моделируют колебания цен на фондовых рынках. Можно поиграть онлайн http://gametheory.cs.ubc.ca/twothirdsavg. Ведь, чтобы хорошо сыграть в указанные игры нужно уметь предугадать, как сыграют другие игроки, т. е. учитывать поведенческий фактор. Это же делают менеджеры на рынке ценных бумаг: они покупают акции, которые будут дорожать в перспективе, или, другими словами, те акции, по которым, по их мнению, другие инвесторы примут решение, что они должны стоить больше через какое-то время. Другими словами, их подход основан не на истинной стоимости акций, а на теории о том, как могут вести себя участники торгов. То есть, так же, как и в описанных выше и играх, они опираются на поведенческий фактор.
Целью настоящей работы являлось сравнительная оценка уровня аналитического мышления обучающихся МОУ СОШ № 75 имени И. М. Халатникова с помощью игры «Гарвард». В соответствие с заявленной целью были поставлены следующие задачи: 1) проведение игры «Гарвард» среди обучающихся различных возрастных групп с различным уровнем математической подготовки, 2) обработка и анализ полученных результатов методами математической статистики, 3) поиск взаимосвязи между результатами, полученными игроками, и уровнем их математической подготовки.
В игре приняли участие обучающиеся 6–11 классов МОУ СОШ № 75 имени И. М. Халатникова. Общее количество обучающихся, принявших участие в игре, составило n = 195 человек. В первую очередь стоит отметить, что значение половины среднего арифметического по всей совокупной группе составило 22. Отклонение полученного результата от 25 означает, что не все игроки играли наугад. Значение ā /2 не хуже аналогичного значения 18–27, полученного в вузах средней руки, не отличающихся сильной математической подготовкой [3]. На рис. 1 изображена гистограмма, демонстрирующая количество игроков, написавших числа из определенного диапазона. Распределение на рис.1 далеко от равномерного, которого следовало бы ожидать в случае, если бы игроки играли наугад. Максимум этого распределения приходится на диапазон 11–20. Этим значениям ā /2 отдала предпочтение большая часть играющих — 34 человека (17 %). Неожиданно, значительная часть играющих — 86 игроков (44 %) отдала предпочтение числу больше 50. Это может свидетельствовать о том, что эти обучающиеся не поняли правил игры, или не смогли аналитически оценить ситуацию, или же просто не захотели играть.
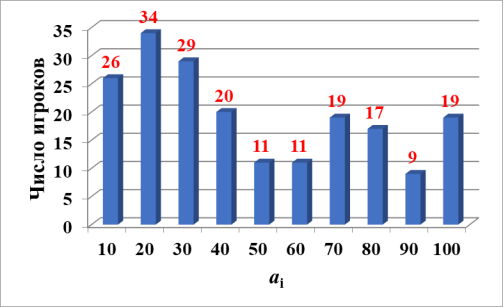
Рис. 1. Гистограмма, демонстрирующая количество игроков, написавших числа определенного диапазона
В противовес этому заметная часть играющих — 26 человек (13 %) выбрала значение ā /2 из интервала 1–10, как в наиболее математически интеллектуальных студенческих коллективах Независимого московского и Гарвардского университетов [3]. Однако победителями стали игроки не этой группы. Победили в игре две девочки, написавшие число 22, точно совпадающее со значением ā /2 по всей группе играющих. Одна из них — одиннадцатиклассница с пятеркой по математике. Другая — семиклассница с четверкой по математике.
После группировки игроков по баллам по математике оказалось, что связь между оценкой по математике и значением половины среднего арифметического ā /2 в данной группе игроков отсутствует (рис. 2). Вариации величины ā /2 не систематичны и изменяются в диапазоне ± 0.22 (изменение в 1 %). Другими словами, как ни парадоксально, троечники играют в игру «Гарвард» не хуже отличников. Заметим, что подобный результат был получен ранее для групп студентов РУТ МИИТ [3].
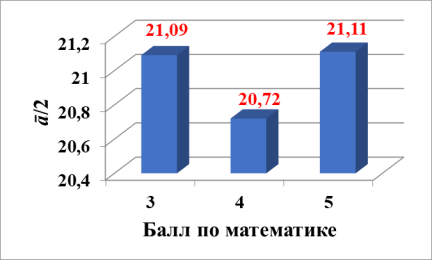
Рис. 2. Зависимость значения половины среднего арифметического ā /2 для игроков 6–11 классов от балла по математике
С чем это связано сказать сложно, но, видимо, результат игры определяется не столько знанием математики, сколько умением стратегически мыслить. С одной стороны, конечно, необходимо знать формулу среднего арифметического, но, как оказалось, для данной игры этого недостаточно, необходимо стратегическое мышление, по показателю которого троечники совершенно не уступают хорошистам или отличникам.
Далее обучающиеся были перегруппированы по классам (рис. 3).
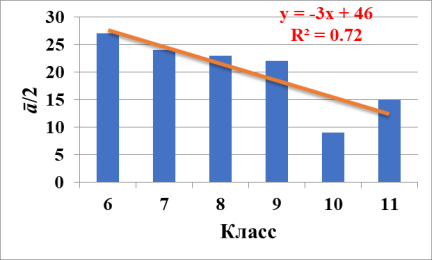
Рис. 3. Зависимость значения половины среднего арифметического ā /2 от класса
Оказалось, зависимость величины ā /2 от класса имеет выраженный нисходящий тренд. Чем старше класс, тем меньше значение ā /2 в классе, т. е. лучше результат игры. Этот нисходящий тренд с высокой достоверностью R 2 = 0.72 задается уравнением y = –3 x +46. В подгруппе 6–9 классов величина ā /2 убывает примерно на 1 пункт каждый год. А достоверность линейного тренда, описываемого уравнением y = –1.6 x +36, достигает R 2 = 0.92. Этот результат в совокупности с предыдущим может означать, что стратегическое мышление, регистрируемое с помощью игры «Гарвард», определяется не столько знаниями в области математики, сколько возрастом.
Неожиданный результат был получен при гендерной группировке. В подгруппе мальчиков значение половины среднего арифметического ā /2 составляет 20, что на 13 % ниже, чем в подгруппе девочек, где ā /2 составляет 23 (рис. 4).
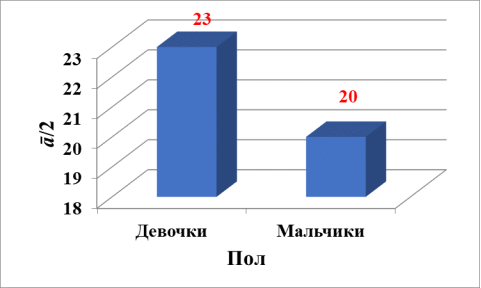
Рис. 4. Значения половины среднего арифметического ā /2 в подгруппах обучающихся мужского и женского пола
Т. е. мальчики в игру «Гарвард» сыграли заметно лучше. Мы не думаем, что эта разница обусловлена разницей в стилях мышления мужчин и женщин. Например, когда игра проводилась среди студентов РУТ МИИТ, напротив девочки сыграли заметно лучше [3]. Возможно, подобный результат связан с тем, что мальчики на этот раз оказались более мотивированы при проведении игры, отнеслись с большей ответственностью к ней и здоровым спортивным интересом. Напомним, что при этом при всем, победили в игре все-таки две представительницы прекрасного поля.
Таким образом, оказалось, что связь между оценкой по математике и значением половины среднего арифметического ā /2 в данной группе игроков отсутствует. Другими словами, троечники играют в игру «Гарвард» не хуже отличников. Видимо, результат игры определяется не столько знанием математики, сколько умением стратегически мыслить, по показателю которого троечники, как оказалось, не уступают хорошистам или отличникам. Группировка обучающихся по классам показала выраженный нисходящий тренд величины половины среднего арифметического ā /2 с ростом класса. Чем старше класс, тем меньше значение ā /2 в классе, т. е. лучше результат игры. Этот результат в совокупности с предыдущим может означать, что стратегическое мышление, регистрируемое с помощью игры «Гарвард», определяется не столько знаниями в области математики, сколько возрастом. В заключение обратим внимание еще раз, что в игре важно как аналитическое мышление, позволяющее понять тактику игру, так и стратегическое, позволяющее оценить, сколько еще играющих так понятливы, как и Вы.
Литература:
1. Нейман, Дж. фон. Теория игр и экономическое поведение / Дж. Фон Нейман, О. Моргенштерн. — Москва: Наука, 1970. — 708 c. — Текст.
2. Gass, S. I. What is game theory and what are some of its applications? / S. I. Gass, R. H. Smith. — Текст // Scientific American. — 2003. — June 2.
3. Кривич, А. С. Реализация игры «Гарвард» в Юридическом институте Российского университета транспорта / А. С. Кривич. — Текст // Вестник Юридического института МИИТ. — 2021. — № 1 (33). — С. 96–103.










