Аналитический и компьютерный подходы к решению приведенных квадратных уравнений в условиях сельской общеобразовательной школы (на примере МБОУ СОШ № 1 с. Аскино Республики Башкортостан)



Уравнения в школьном курсе алгебры занимают одно из ведущих мест любого учебно-методического комплекта. На их изучение отводится гораздо больше времени, чем на любую другую тему школьного курса математики [1].

Квадратные уравнения начинают изучать уже во втором полугодии 8 класса, согласно выбранному учебному плану школы и календарно-тематическому планированию учителя на основе авторского учебника.

К изучению этой темы обучающиеся приступают, уже накопив определенный опыт, а также владея достаточно большим запасом алгебраических, геометрических и общематематических представлений, понятий и умений.

При изучении и дальнейшем закреплении материала по данной теме вырабатываются умения решать определенным методом квадратные уравнения [2] и простейшие рациональные уравнения [3], а также применять их к решению задач.

Это способствует пониманию таких понятий, как квадратное уравнение [4], неполное квадратное уравнение [4], приведенное квадратное уравнение [5], выводам формулы дискриминанта [6] и корней квадратного уравнения [7], теоремы Виета [8] и обратной ей, знакомству с дробно-рациональными уравнениями [9], а также с различными способами решения.

В ходе изучения происходит понимание того, что уравнение есть аппарат решения многих разнообразных задач математики, а еще всевозможных смежных областей знаний и межпредметных дисциплин.

Однако, до сих пор обучающиеся сельских общеобразовательных школ испытывают затруднения при изучении данной темы в курсе средней общеобразовательной школы.

Цель исследования. В связи с этим, целью данной работы является анализ и сравнение учебников алгебры разных авторов по теме «Квадратные уравнения» , а также проведение компьютерного эксперимента по нахождению корней приведенного квадратного уравнения в среде школьного языка программирования Паскаль на базе сельской общеобразовательной школы МБОУ СОШ № 1 с. Аскино Республики Башкортостан.

Тема актуальна не только для обучающихся среднего и старшего школьного звена обучения, но и учителей-предметников при подготовке уроков по данной теме.

Краткий анализ авторских учебников и методов решения приведенного квадратного уравнения с указанными коэффициентами.

Анализ авторского учебника № 1

Рассмотрим некоторые особенности решения квадратных уравнений по учебнику алгебры для 8 класса под редакцией авторов [10], предусмотренных ФГОС [11].

Изучение темы «Квадратные уравнения» начинается с пункта «Неполные квадратные уравнения» . Здесь вводятся понятия квадратного уравнения, приведённого квадратного уравнения, неполного квадратного уравнения, приводятся названия коэффициентов a , b и c в уравнении вида ax ² + bx + c = 0, где a ≠ 0, и указываются в различных квадратных уравнениях.

В заданиях систематизируются известные обучающимся приёмы решения неполных квадратных уравнений, которые находят непосредственное применение на практике при решении соответствующих примеров, а также сталкиваясь с подобными задачами в предметах естественнонаучного цикла (геометрия, физика, химия, биология, астрономия).

Мы выявили, что принципиально новым для обучающихся шагом является решение текстовых задач с помощью неполных квадратных уравнений. При выполнении упражнений они убеждаются в важности формируемых умений. Здесь обучающиеся впервые встречаются с ситуацией, когда один из найденных корней уравнения не соответствует смыслу задачи. Конечно, для многих школьников она является абсурдной и странной.

Следующий пункт учебника «Формула корней квадратного уравнения» посвящён квадратным уравнениям общего вида. Сначала рассматривается решение полного квадратного уравнения с числовыми коэффициентами. Далее все выкладки повторяются для уравнения вида ax ² + bx + c = 0 с буквенными коэффициентами a , b и c , отличными от нуля, и выводится общая формула корней. Обучающиеся овладевают умением решать квадратные уравнения, используя соответствующую последовательность шагов:

1) вычисляют дискриминант квадратного уравнения по формуле D = b ² – 4ac ;

2) при

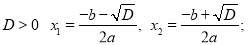
3) при

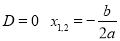
4) при делается вывод, что корней нет.

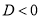
Из общей формулы корней квадратного уравнения выводится формула корней квадратного уравнения ax ² + 2 kx + c = 0 с чётным вторым коэффициентом.

Необходимо отметить, что умение решать квадратные уравнения с помощью общей формулы корней или формулы корней квадратного уравнения с чётным вторым коэффициентом относится к числу важнейших умений, формируемых в курсе алгебры.

Внимание обучающихся обращается на то, что при решении квадратных уравнений с помощью общей формулы корней квадратного уравнения или формулы корней квадратного уравнения с чётным вторым коэффициентом часто бывает удобно упростить уравнение при помощи выполнения некоторых преобразований: (1) умножить все члены уравнения на –1 , если первый коэффициент отрицателен, (2) избавиться от дробных коэффициентов, умножив все члены уравнения на общий знаменатель дробей, (3) сократить все члены уравнения на одно и то же число, если это возможно. Большое внимание уделяется теореме Виета и обратной ей при изучении приведенных квадратных уравнений.

Полагаем, что положительными сторонами данного авторского учебника можно назвать подробное изложение теоретической части, грамотная подача материала, разбор довольно сложных примеров заданий.

Рассмотрим пример решения квадратного уравнения вида 8 x ² + 2 x — 1 = 0 с коэффициентами a = 8, b = 2, c = –1. Согласно приведенной в учебнике методике вычислим дискриминант квадратного уравнения D .

D =b ² –4 · a · c = 2 ^2– 4 · 8 · (–1) = 4 + 32 = 36.

Согласно анализу дискриминанта видим, что D > 0. Значит, мы можем применить формулу корней квадратного уравнения и вычислить численные значения.

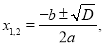
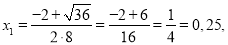
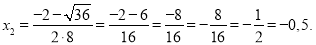
Ответ: x ₁ = 0,25, x ₂ = –0,5.

Анализ авторского учебника № 2

В следующем авторском учебнике [12] тема квадратных уравнений разбита на следующие основные блоки в соответствии с теоретическим материалом: (1) Отработка основных понятий, связанных с квадратными уравнениями; (2) Неполные квадратные уравнения; (3) Полные квадратные уравнения (алгоритм решения квадратного уравнения по формулам дискриминанта, нахождения корней, изучение и использование теоремы Виета); (4) Рациональные уравнения (алгоритм решения рационального уравнения; решение рациональных уравнений методом введения новой переменной, биквадратные уравнения); (5) Текстовые задачи, решаемые с помощь рациональных уравнений.

Мы выявили, что при изложении материала используются определения и теоремы; подробно разобраны примеры, замечания по решению примеров и задач, а также алгоритмы решения уравнений; имеются вопросы для самопроверки, а также в конце каждой главы прописаны основные результаты и темы исследовательских работ.

На наш взгляд, наиболее положительные качества учебника следующие: доступный и понятный стиль изложения, классификация задач по трем уровням сложности, наличие рисунков и чертежей для наглядного представления теоретического и задачного материала, задачи на повторение. Среди недостатков можно выделить наиболее значимый: материал представлен в двух книгах.

Примечательно то, что в указанных двух последних авторских учебниках [11] и [12] рассматривается решение систем квадратных параметрических уравнений [13], чего не наблюдается в учебниках других авторов.

Решим приведенное квадратное уравнение вида x ² + 16 x + 63 = 0 с применением теоремы, обратной теореме Виета. Коэффициент уравнения a = 1, b = 16, c = 63.

Видим, что коэффициент p = 16, свободный член q = 63. Значит, согласно теореме, сумма корней равна –16, а их произведение составляет 63. Подберем такие корни x ₁ = –7, x ₂ = –9. Действительно, сумма ( x ₁ + x ₂ ) = –7 + (–9) = –7 –9 = –16, а произведение ( x ₁ · x ₂ ) = (–7) · (–9) = 63. Таким образом, можем утверждать, что корни подобрали верно.

Ответ: x ₁ = –7, x ₂ = –9.

Анализ авторского учебника № 3

Наконец, в учебном пособии автора [14], предусмотренное ФГОС основного общего образования, изучение темы начинается с определения квадратного уравнения, приведенного квадратного уравнения, которые решаются путем выделения квадрата двучлена [15]. Далее предлагается формула корней квадратного уравнения, понятия дискриминант, числа корней квадратного уравнения.

В этом пособии большое количество примеров на решение уравнений способом замены переменной [16], то есть приведение к квадратным уравнениям. Целый пункт отведен для решения квадратных уравнений по второй формуле (с четным коэффициентом).

Достаточно большое внимание уделяется решению задач на применение формулы корней квадратного уравнения. Затем рассматриваются неполные квадратные уравнения и теорема Виета.

Мы считаем, что темы в данном учебнике представлены конкретно и точно, имеется внушительный объем заданий для практического применения на уроках алгебры.

Заканчивается изучение темы «Квадратные уравнения» представлением раздела «Разложение квадратного трехчлена на множители» . Авторы учебника в разделе «Для тех, кому интересно» предлагают довольно интересный приём бесформульного решения квадратного уравнения, что является, на наш взгляд, своего рода альтернативой стандартным методикам других составителей.

Рассмотрим примеры решения двух квадратных уравнений из этого авторского учебника x ² –12 x + 36 = 0 и 7 x ² –25 x + 23 = 0:

а) x ² –12 x + 36 = 0.

Коэффициенты a = 1, b = –12, c = 36.

Вычислим дискриминант D согласно известной формуле:

D = b ² –4 ac = (–12) ^2– 4 · 1 · 36 = 144–144 = 0.

Согласно анализу дискриминанта видим, что D = 0.

Применим формулу корней квадратного уравнения:

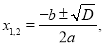
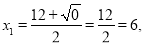
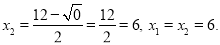
Покажем, что корни уравнения найдены правильно. В уравнении x ² –12 x + 36 = 0 коэффициент p = –12, а свободный член q = 36. Сумма найденных чисел ( x ₁ + x ₂ ) = 6 + 6 = 12, а их произведение ( x ₁ · x ₂ ) = 6 · 6 = 36. Значит, по теореме, обратной теореме Виета, эти числа являются корнями уравнения x ² –12 x + 36 = 0.

Ответ: x = 6.

б) 7 x ² –25 x + 23 = 0.

Коэффициенты a = 1, b = –12, c = 36.

Также вычислим дискриминант D согласно известной формуле:

D = b ² –4 ac = (–25) ² –4 · 7 · 23 = 625–644 = –19.

Согласно анализу дискриминанта видим, что D < 0.

Ответ: корней нет.

Таким образом, при сравнении всех трех авторских учебников, имеющихся в школьной библиотеке МБОУ СОШ № 1 с. Аскино Республики Башкортостан, можно сделать текущий вывод о том, что материал по квадратным уравнениям во всех рассмотренных учебно-методических комплектах изложен доступно и понятно.

Большое внимание уделено как теоретической, так и практической части, ведь важно уметь применять полученные знания в решении уравнений, задач, где математическими моделями выступают дробные рациональные уравнения.

Задания у всех авторов учебников очень многообразны и направлены на исследование уравнений, на определение количества решений, а также нахождение корней.

Компьютерный эксперимент по нахождению корней приведенного квадратного уравнения . В целях подтверждения правильности решения всех вышеприведенных квадратных уравнений из разных авторских учебников по алгебре, мы разработали программу на школьном языке программирования PascalABC.NET [17] по нахождению корней приведенного квадратного уравнения, исходя из анализа дискриминанта.

Данная идея возникла на основании того, что в курсе информатики 8 класса авторского учебника [18], предусмотренного ФГОС, при программировании разветвляющихся алгоритмов в главе «Основы алгоритмизации» затрагивается составной оператор, что позволяет написать программу для проведения анализа квадратного уравнения.

Ниже приводим листинг программы на указанном языке программирования с учетом применения неполной условной конструкции ветвления [19], комментарий к каждой строке, указанием всех ключевых служебных слов языка и «хвостика» дробной части.

Запустим программу для нахождения корней приведенного квадратного уравнения, указанных выше, введя коэффициенты и получив протоколы работы.

Таким образом, на основе разработанного шаблона программы, мы можем провести анализ любого квадратного уравнения, вычислить дискриминант по указанным коэффициентам и, соответственно, корни. Следует добавить, что аналитический и компьютерный подходы к решению квадратных уравнений полностью дополняют друг друга.

Это означает, что грамотно составленная аналитическая (математическая) модель любого из приведенных авторских учебников, позволяет разработать алгоритм правильного решения квадратного уравнения.

В свою очередь, математическая модель плавно переходит в запись программного кода на одном из учебных языков программирования и позволяет провести компьютерный эксперимент даже в рамках сельской общеобразовательной школы, что очень важно для обучающихся из периферии. Не секрет, что доступного и качественного компьютерного оборудования до сих пор нет во многих сельских и деревенских школах.

Выводы и заключение . Таким образом, в ходе проведенного анализа имеющихся в наличии школьных учебников алгебры 8 класса, мы выявили и остановились на том, что наиболее оптимальный для восприятия обучающихся сельских школ и периферии, является авторский учебник под редакцией С. А. Теляковского [10].

Для нас, обучающихся 8 класса, важно уметь применять и аналитический, и компьютерный подходы к решению приведенных квадратных уравнений, что является основой для создания базиса при подготовке к основному государственному экзамену.

Литература:

1. Старостина, А.Е., Винокурова, С. З. Формирование математических понятий в школьном курсе математики (на примере изучения темы «Квадратные уравнения»). // Обучение и воспитание: методики и практика 2016/2017 учебного года. — Сборник материалов XXXIII Международной научно-практической конференции. — Новосибирск: Издательство «ООО Центр развития научного сотрудничества», 2017. — С.99–103.

2. Рахманова, Х. Б. Решение квадратного уравнения. // Наука, образование и инновации. — Сборник статей Международной научно-практической конференции, 2016. — Уфа: Издательство «ООО Омега Сайнс», 2016. — С.16–18.

3. Смышляева, Т. А. Урок алгебры в 8 классе по теме «Решение рациональных уравнений». // Научный журнал «Азбука образовательного пространства». — №.2(3). — Марий Эл: Издательство «Негосударственное образовательное частное учреждение дополнительного профессионального образования Экспертно-методический центр», 2018. — С.31–32.

4. Квадратное уравнение. Материал из Википедии — свободной энциклопедии. // URL: https://ru.wikipedia.org/wiki/Квадратное_уравнение (дата обращения 20.03.2022).

5. Приведенный многочлен. Материал из Википедии — свободной энциклопедии. // URL: https://ru.wikipedia.org/wiki/Приведённый_многочлен (дата обращения 20.03.2022).

6. Дискриминант. Материал из Википедии — свободной энциклопедии. // URL: https://ru.wikipedia.org/wiki/Дискриминант (дата обращения 20.03.2022).

7. Уравнение. Материал из Википедии — свободной энциклопедии. // URL: https://ru.wikipedia.org/wiki/Уравнение (дата обращения 20.03.2022).

8. Формулы Виета. Материал из Википедии — свободной энциклопедии. // URL: https://ru.wikipedia.org/wiki/Формулы_Виета (дата обращения 20.03.2022).

9. Рациональная функция. Материал из Википедии — свободной энциклопедии. // URL: https://ru.wikipedia.org/wiki/Рациональная_функция (дата обращения 20.03.2022).

10. Макарычев, Ю.Н., Миндюк, Н.Г., Нешков, К.И., Суворова, С. Б. Алгебра. 8 класс. Учебник для общеобразовательных организаций с приложением на электронном носителе. // Под редакцией Теляковского С. А. — М.: Издательство «Просвещение», 2013. — 287 с.

11. Ванюкова, Е. С. ФГОС на уроках математики. Структура урока по ФГОС. // Вестник научных конференций. — № 1–5(17). — Тамбов: Издательство «ООО Консалтинговая компания Юком», 2017. — С.51–53.

12. Мордкович, А. Г. Алгебра. 8 класс. Учебник для учащихся общеобразовательных учреждений. В 2-х частях. — Ч.1. — М.: Издательство «Мнемозина», 2010. — 215 с.

13. Сикорская, Г. А. О решении квадратных уравнений, содержащих параметр. // Научный журнал «Научный альманах». — № 9–1(71). — Оренбург: Издательство «ООО Консалтинговая компания Юком», 2020. — С.100–105.

14. Дорофеев, Г.В., Суворова С. Б., Бунимович Е. А. и др. Алгебра. 8 класс. Учебник для общеобразовательных организаций. — М.: Издательство «Просвещение», 2016. — 320 с.

15. Кара-Сал, Н. М. Использование приема выделения полного квадрата при решении некоторых математических задач в школе. // Вестник Тувинского государственного университета. № 4 Педагогические науки. — Т.4. — № 4(19). — Тува: Издательство «ФГБОУ ВПО Тувинский государственный университет», 2013. — С.138–152.

16. Фирстова, Н. И. Обучение решению алгебраических уравнений методом замены переменной. // Научный журнал «Наука и школа». — № 5. — М.: Издательство «Московский государственный педагогический университет», 2019. — С.144–155.

17. PascalABC.NET. Материал из Википедии — свободной энциклопедии. // URL: https://ru.wikipedia.org/wiki/PascalABC.NET (дата обращения 27.03.2022).

18. Босова, Л.Л., Босова, А. Ю. Информатика. Учебник для 8 класса. — М.: Издательство «БИНОМ. Лаборатория знаний», 2013. — 155 с.

19. Миниахметов, А. А. Роль учебного блока «ветвление» при подготовке выпускников сельских общеобразовательных школ к ЕГЭ по информатике и ИКТ. // Theoretical & Applied Science. — 2015. — № 3(23). — С.63–68. — DOI 10.15863/TAS.2015.03.23.13.