Математика кубика Рубика



В статье автор повествует об истории одной из старейших головоломок, кубике Рубика. Рассматривает механизмы его сборки и взаимосвязь с математикой, а также приводит математическое доказательство существования алгоритма решения данной головоломки.

Ключевые слова: кубик Рубика, комбинаторика, головоломка, число Бога, грани, поворот.

С давних времен существует головоломка, называющаяся кубиком Рубика. Мне кажется многим были бы интересны способы её решения (сборки), её происхождение, и взаимосвязь с математикой. Исходя из этого, сформулируем следующую цель.

Цель работы — узнать, что такое кубик Рубика, его составляющие части и способы сборки.

Для достижения данной цели, были поставлены следующие задачи:

1. Узнать историю кубика Рубика и что под ним понимают;

2. Изучить математику кубика Рубика;

3. Разобрать алгоритм сборки.

Кубик Рубика

Кубик Рубика или «волшебный кубик» — это механическая головоломка, изобретенная в 1974 году (однако запатентована она была только в 1975 году) венгерским скульптором и преподавателем архитектуры Эрне Рубиком [1].

Головоломка представляет собой пластиковый куб 3x3x3 (оригинал) с 54 видимыми цветными наклейками. Грани большого куба способны вращаться вокруг 3 внутренних осей куба. Каждая из шести граней состоит из девяти квадратов и окрашена в один из шести цветов, в один из распространенных цветовых вариантов, расположенных попарно, напротив друг друга: красно -оранжевый, бело — желтый, сине — зеленый (рис. 1).

Рис. 1. Куб Эрне Рубика

Вращение граней позволяет вам переставлять цветные квадраты различными способами. Задача состоит в том, чтобы «решить кубик Рубика»: поворачивая грани куба, вернуть его в исходное состояние, когда каждая из граней состоит из квадратов одного цвета.

Патентная история

История кубика Рубика началась в марте 1970 года, когда Ларри Николс изобрел куб-головоломку с вращающимися частями, собранными на магнитах (рис. 2).

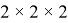
Рис. 2. Куб Ларри Николса

11 апреля 1972 года Николс получил патент на свое изобретение. 9 апреля 1970 года Фрэнк Фокс подал заявку на сферическую головоломку размером 3 × 3 × 3 и получил патент 16 января 1974 года. В середине 1970-х Эрно Рубик преподавал студентам математическую теорию групп. Однако, исходя из технологий тех лет, студентам было очень тяжело. Однажды, чтобы визуализировать процесс обучения, Рубик сделал 27 деревянных кубиков и раскрасил каждый в шесть цветов. Он столкнулся с трудностью собрать их в один куб так, чтобы каждая грань была окрашена в свой цвет. Более того, он сидел над этой задачей целый месяц. 30 января 1975 года Э. Рубик получил патент на свое изобретение «Волшебный кубик».

Механизм

Из центрального и ребристого элементов вырезают фрагмент изнутри таким образом, чтобы получилась полость в виде соединения трех цилиндров. Кроме того, на краевых и угловых элементах имеются выступы особой формы. Эти выступы образуют фрагмент цилиндра, который плотно входит в полость. Благодаря такой конструкции грани куба свободно вращаются. В центре конструкции вместо «невидимого кубика» находится трёхмерная крестовина, на которой свободно вращаются центральные элементы. Все остальные элементы держатся друг за друга, входя выступами в вышеуказанную выемку (рис. 3).

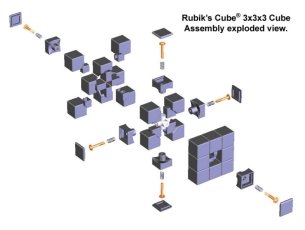
Рис. 3. Устройство кубика Рубика

Комбинаторика

Здесь и ниже под кубиком Рубика мы подразумеваем исходный куб 3×3×3.

Количество различных состояний кубика Рубика определяется порядком группы , являющейся подгруппой , порождаемой шестью поворотами граней:

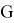
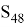
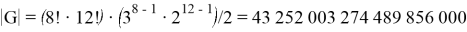
Это число не учитывает разную ориентацию центральных квадратов.

С учётом ориентации центральных квадратов количество состояний возрастает в раз, и по итогу мы получаем состояний.

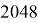
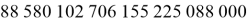
Однако при сборке ориентация центральных квадратов обычно игнорируется, потому что. На большинстве кубиков нет отметок, чтобы отследить их.

Математика кубика Рубика

Существует множество алгоритмов, предназначенных для перевода кубика Рубика из произвольной конфигурации в конечную конфигурацию (конечная конфигурация означает собранный куб, удовлетворяющий условиям, описанным выше) (рис. 4).

Рис. 4. Конечная и произвольная конфигурации

Алгоритм, который решает головоломку за как можно меньшее количество ходов, называется Божьим алгоритмом. Алгоритм бога головоломки — это любой алгоритм, который выдает решение головоломки, содержащее минимально возможное количество ходов, начиная с любой заданной конфигурации.

Число Бога для головоломки — это число n, такое, что существует по крайней мере одна конфигурация головоломки, оптимальное решение которой состоит из n ходов, и нет конфигурации, длина оптимального решения которой превышает n. Другими словами, число Бога — это наименьшая верхняя граница множества длин оптимальных решений конфигураций головоломок. Число Бога для Кубика Рубика равно 20. Работа по решению головоломки ведется в двух направлениях:

– Развитие скорости, оттачивание моторики.

– Математические расчеты

Минимальное количество ходов, необходимое для решения кубика Рубика, до сих пор неизвестно. Количество фильмов, которые позволили бы решить любой вариант головоломки, не определено. Многие верят, что без божественного вмешательства не обойтись, отсюда и возникает число Бога.

В 1981 году доктор М. Тислтуэйт доказал, что для решения любого варианта головоломки требуется не более 52 движений. Таким образом, он подошел к вычислению числа Бога. В июне 2010 года команда из четырех ученых доказала, что любой вариант «шифрования» кубика Рубика может быть решен за 20 ходов. Организованный этими энтузиастами сайт содержит передовые алгоритмы для решения головоломки [2].

Осталось только вычислить, сколько из общего количества комбинаций ( ) распутывается определенным количеством ходов. Например, число позиций, для решения которых требуется один ход, — 18. Это легко подсчитать: есть 6 граней и 3 способа скручивания каждой.

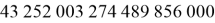
Также нетрудно вычислить, сколько вариантов решается с помощью двух или трех ходов. Но по мере увеличения их количества усложняется подсчет. На сегодняшний день математики остановились на 16 ходах. До 20 осталось немного. И это последние нерешенные моменты для кубика Рубика.

Алгоритм сборки

Итак, грани кубика Рубика могут крутиться:

– По часовой стрелке;

– Против часовой стрелки.

Если движение грани в формуле описано как «против часовой стрелки», около буквы будет штрих (‘). Если «по часовой» — просто буква название грани.

Описания названий граней в формулах:

– L — Left, левая грань;

– R — Right, правая грань;

– U — Up, верхняя грань;

– F — Front, передняя грань;

– D — Down, нижняя грань;

– B — Back, задняя грань.

Рассмотрим алгоритм сборки на следующем рисунке (рис. 5) [3]

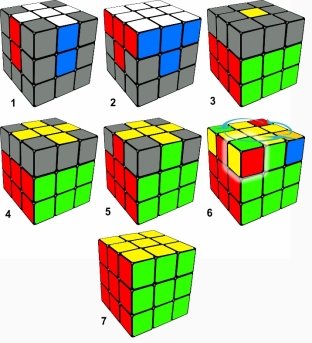
Рис. 5. Алгоритм сборки

1. Собирается правильный крест на белой грани (1)
2. Собрать углы белой грани (2)

– Переворачиваем кубик Рубика белым крестом вниз;

– Подводим бело-сине-красный угол напротив его места на белой грани (между синим и красным центрами);

– Берем кубик в руки, где в нашем случае грань с зеленым центром будет перед нами.

– Делаем формулу из 4 движений . Другими словами: правая грань от себя + верхняя по часовой + правая на себя + верхняя против часовой. Делать нужно эту формулу от 1 до 5 раз, не меняя положение кубика в руках, пока угол не встанет на свое место.

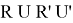
3. Собираем средний слой кубика Рубика (3)

– Ребро будет находиться либо в среднем, либо в верхнем слое. Расставлять нужно ребра, у которых нет в составе желтого элемента, то есть: красно-зеленое, зелено-оранжевое, оранжево-синее, сине-красное.

– Делаем следующее:

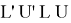
– Подводим ребро под центр, соответствующий одному из элементов ребра. Затем нам нужно понять в какую сторону должно уйти наше ребро (влево или вправо).

– Если ребро должно уйти вправо, делаем следующий алгоритм действий

• ;
• 
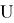
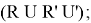
• Перехват кубика по часовой стрелке, то есть если сейчас кубик смотрит к вам красным центром, то просто перехватите его (без поворота граней) так, чтобы он смотрел на вас зеленым центром;
• 

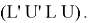
– Если ребро должно уйти влево, то

• ;
• 
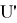
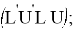
• Перехват кубика против часовой стрелки;
• 

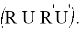
– Тоже самое делаем и с остальными ребрами.

4. Собираем крест на желтой грани (4)

– Если крест готов — переходим к шагу 5.

– Если другой элемент, делаем формулу .

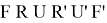
– Смотрим, есть ли крест. Если нет — делаем эту формулу еще раз.

– В конечном итоге, получится крест на желтой грани.

5. Собираем правильный крест на желтой грани (5)

– Ворочаем верхнюю грань так, чтобы центры боковых граней совпали с ребрами верхней грани напротив или рядом;

– Если центры совпали рядом, берем кубик так, чтобы они стояли справа и сзади.

– Если напротив — спереди и сзади.

– Делаем формулу ;

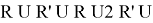
– При необходимости повторяем формулу еще раз.

6. Расставляем углы верхнего слоя по местам

– Это делается формулой .

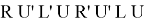
– Перед тем, как сделать эту формулу, нужно посмотреть есть ли уже стоящий на месте угол. Если есть — ставим этот угол справа от себя и делаем формулу столько раз, сколько понадобится, чтобы оставшиеся три угла встали на места.

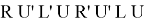
– Если на месте нет ни одного угла — также делаем формулу . В результате должен появиться 1 угол, стоящий на своем месте. Далее ставите этот угол справа от себя и снова делаете формулу

, но уже столько раз, сколько понадобится, чтобы оставшиеся три угла встали на места.

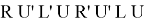
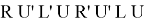
7. Разворачиваем углы верхнего слоя (6)

– Берем кубик желтой гранью вверх, неправильно повернутым углом справа от себя;

– Делаем формулу 2 или 4 раза. Угол, который стоял справа, повернется правильно.

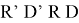
– Держим кубик в том же положении, но крутим верхнюю грань так, чтобы следующий неправильно повернутый угол встал справа от нас;

– Делаем формулу 2 или 4 раза.

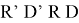
– Подставляем оставшиеся углы;

– Делаем формулу 2 или 4 раза.

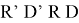
8. Задача решена (7)

Математическое доказательство алгоритма кубика Рубика

Можно ли доказать, что не существует алгоритма, который позволяет перевернуть один крайний куб, не перемещая другой блок? Да, такое доказательство существует и выглядит примерно так.

Когда грань поворачивается, 4 крайних блока перемещаются. Соответственно, вам нужно сделать 10 ходов для каждого элемента. В то же время вам нужно подсчитать количество действий. Затем вам нужно сложить числа для каждого блока на краю. Общее количество ходов должно быть 40, так как каждый из 10 ходов увеличивает их общее количество на 4.

Соответственно, сумма перемещений для элементов, расположенных по краям, должна быть кратна четырем.

В то же время, если блок на краю переместится четное число раз и вернется на свое место, он будет иметь ту же ориентацию. И наоборот, если элемент перемещен нечетное количество раз и помещен на место, он будет перевернут. Все вышеперечисленные алгоритмы могут быть легко протестированы на практике

Теперь стоит рассмотреть схему, которая предполагает поворот одного элемента на месте, без привлечения других. В то же время один блок был перемещен четное число раз, в то время как каждый из остальных 11 элементов был перемещен на нечетное число. Сумма 11 четных чисел и одного нечетного числа всегда нечетна. И ранее было установлено, что оно должно быть кратно 4. Мы получаем противоречие. Следовательно, первоначальное предположение неверно.

Вывод

этой статье была рассмотрена история головоломки — кубика Рубика, математическое обоснование существования алгоритма решения головоломки и дан конкретный вариант сборки.

Литература:

1. Э. Рубик. Кубик Рубика. За гранями головоломки, или природа творческой мысли = Cubed: The Puzzle of Us All / Ernő Rubik; пер. с англ. Д. Маслов, А. Маслов. — М.: Альпина Паблишер, 2021. — 182 с. — ISBN 978–5–907394–81–0.
2. God's Number is 20. — Текст: электронный // A History of God's Number: [сайт]. — URL: https://www.cube20.org.
3. Frey, Alexander; Singmaster, David (1982). Handbook of Cubic Math. Enslow. ISBN 0894900587.