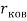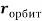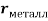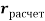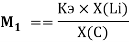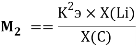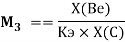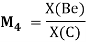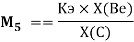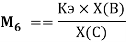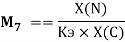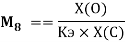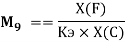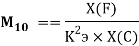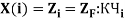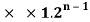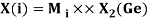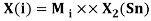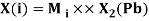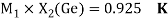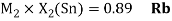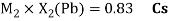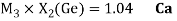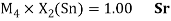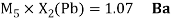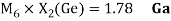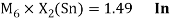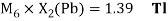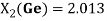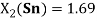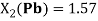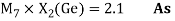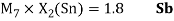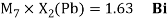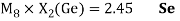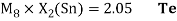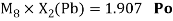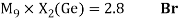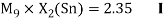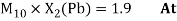Расчет электроотрицательности химических элементов в таблице Д. И. Менделеева



Предложен и обоснован новый метод создания шкалы электроотрицательности (ЭО) химических элементов. В основу данного метода положены общепринятые научные положения — факты, характеризующие основные свойства атомов, и первое правило Полинга. Оценка зависимостей между анализируемыми фактами и формулирование присущих им закономерностей осуществлена с помощью гипотетико-дедуктивного метода. Для расчетов использованы приведенные в научной литературе и измеренные с большой точностью численные значения величин энергии ионизации и радиусов атомов. Представлены математические выражения, позволяющие судить как об ЭО, так и о связях энергии ионизации и других свойств и характеристик атомов. Найденное математическое выражение для расчета ЭО содержит пару взаимосогласованных «Чисел Менделеева», смысл которых раскрыл профессор Сколтеха Артем Оганов. Полученные результаты согласуются с литературными данными.

Ключевые слова : электроотрицательность (ЭО), первое правило Полинга, шкала Полинга, шкала Оллреда-Рохова, шкала Оганова, координационные числа, энергия ионизации, атомные радиусы, опорные элементы.

Впервые понятие и шкалу ЭО ввел Лайнус Полинг в 1932 году как качественную характеристику способности атомов притягивать к себе электроны [1]. На данный момент существует много методов и имеются десятки шкал ЭО, в основу которых положены различные свойства веществ и элементов. Дискуссии о самом понятии ЭО и методов ее определения не дали общепризнанных результатов на поставленные вопросы. По мнению некоторых ведущих ученых [2], ЭО элементов не является строгим физическим понятием, однако оно принято мировым научным сообществом и может быть выражено в численном виде в рамках определенной шкалы. Ряд шкал ЭО имеют размерность физических величин — другие таковой размерности не имеют [1].

Предложенное Полингом выражение для расчета разницы в ЭО между химическими элементами A и B имеет вид:

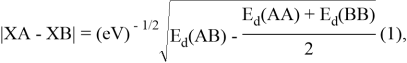
в котором энергии диссоциации связей A — B, A — A и B — B имеют размерность в электрон-вольт. Для выбора произвольной точки отсчета производилось взаимное согласование ЭО с использованием большого числа термохимических данных по энергиям связи. Оно осуществлялось таким образом, чтобы наиболее электроотрицательным элементам от C до F приписать значения от 2.5 до 4.0 [2]. Следует отметить, что Полинг осознанно перевел полученное им значение ЭО в безразмерную величину путем введения коэффициента .

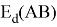
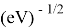
Еще одна шкала, основанная на эффективном заряде ядра атома

и ковалентных радиусах атомов, принадлежит Альберту Л. Оллреду и Юджину Г. Рохову. Считают, что ЭО определяется кулоновской силой притяжения электрона к одному из двух ядер:

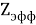
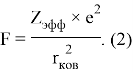
Для приведения в соответствие со шкалой Полинга ими найдено эмпирическое соотношение:

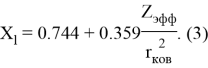
Использование в данном уравнении экспериментальных значений , полученных на основе данных рентгеноструктурного анализа, позволило считать ее как наиболее обоснованную и приемлемую по настоящее время [3].

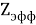
Получение новых результатов экспериментальных исследований и неспособность существующих теорий объяснить происходящие в реальности процессы вызывает потребность как в корректировке существующих шкал ЭО, так и в их кардинальном пересмотре.

В 2021 году Артем Оганов и Кристиан Тантардини пересмотрели и уточнили шкалу ЭО созданную Лайнусом Полингом. В отличие от Полинга Оганов стал считать ЭО не из абсолютной, а из относительной разницы ионной и ковалентной связи. Он изменил формулу Полинга, заменив аддитивную добавку на мультипликативную [4]:

). (4)

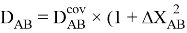
Кроме того, Артем Оганов раскрыл смысл понятия «менделеевское число». В его понимании — это совокупность значений радиуса и ЭО атома в виде одного числа [5]. Как считает Артем Оганов, получена новая шкала ЭО, которая хорошо работает как при маленьких разностях ЭО, так и при больших.

Настоящая работа посвящена созданию новой шкалы ЭО. В ней автор опирается только на научные факты, которые обладают общими и необходимыми специфическими признаками. В качестве таких фактов использовались характеристики свободных атомов, которые представлены в виде простого вещества. А именно:

— энергия ионизации атомов;

— размер атомных радиусов;

— электронные конфигурации атомов.

Выбор данных фактов не случаен. Эти фундаментальные характеристики свободных атомов, в значительной степени определяют их свойства, проявляющиеся в способности отдавать и принимать электроны [2]. При этом, количественным выражением данного свойства служит энергия ионизации, которая в свою очередь функционально связана с размерами радиуса конкретного атома [2].

Примечателен и тот факт, что первые две характеристики для последовательности атомов и значения ЭО для последовательности тех же атомов имеют совпадающую периодичность.

В подавляющем большинстве случаев считается, что определяющую роль играет не весь набор энергий ионизации электронов атома, а только нескольких из первых. Это объясняется именно тем, что первые энергии ионизации атомов сильно коррелируют со значениями величин атомных радиусов. Экспериментально установлено, что атомы больших размеров обычно имеют саму низкую энергию ионизации, а атомы меньших размеров — наоборот.

Кроме этого, при определении информативности ряда характеристик, использовались первое правило Полинга и коррелированность между значениями энергии ионизации и величинами радиусов атомов. Применение в работе первого правила Полинга теоретически подтверждает высокую информативность радиусов атомов и их роль в строении вещества, а сила корреляции характеризует обратную зависимость энергии ионизации от размера атома (атомы самых больших радиусов имеют самую маленькую энергию ионизации и наоборот) [2].

В рамках нашего исследования было принято использовать полные наборы (суммы) энергий ионизации присущие конкретному атому, которые впоследствии нормировались в удобную форму для вычисления ЭО химических элементов. Расчеты осуществлялись начиная со второго периода, который не имеет d-орбитали. Суммирования энергий ионизации осуществлялись с учетом электронных конфигураций разных атомов находящихся в возбужденном состоянии:

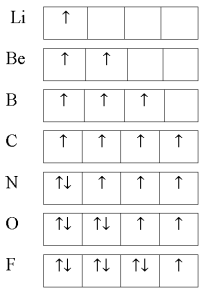
По конфигурации для F, табличным значениям энергии ионизации [8] вычислили суммарное значение энергии ионизации:

.

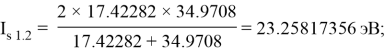
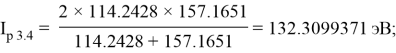
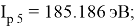
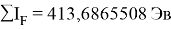
Суммарные энергии ионизации кислорода O, азота N, углерода C, бора B, бериллия Be и лития Li рассчитывают аналогично. Расчеты приведены ниже:

.

.

;

.

.

эВ

.

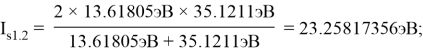
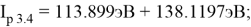
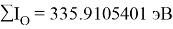
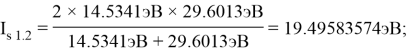
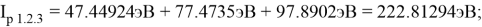
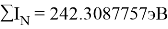
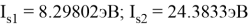
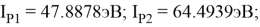
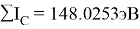
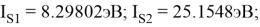
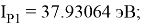
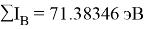
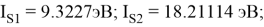
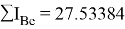
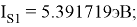
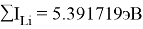
Результаты расчетов:

;

; .

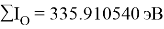
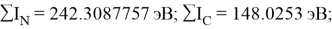
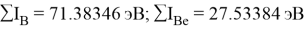
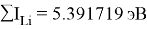
Информативный параметр атома определили из выражения:

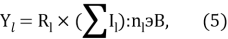
где суммарный потенциал ионизации атома в эВ, n — количество его валентных электронов.

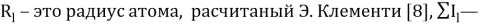
Значения информативных параметров для элементов второго периода равны: = 24.821 эВ, 26.873 эВ, 27.139 эВ, 24.794 эВ, 20.701 эВ,

15.419 эВ, 9.004 эВ.

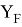
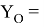
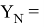
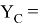
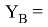
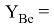
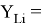
По отношениям информативного параметра атома фтора F к информативным параметрам элементов второго периода судили о силе его воздействия на них:

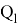
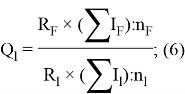
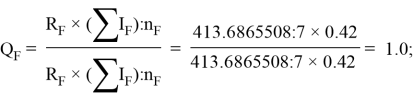
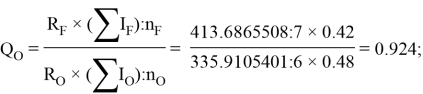
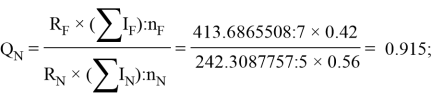
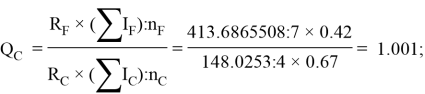
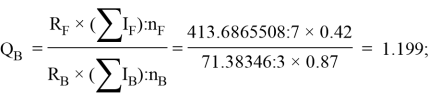
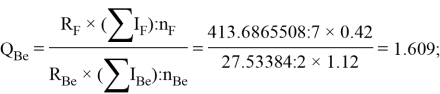
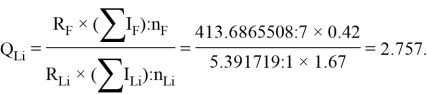
Рассчитанные отношения имеют значения:

1.0, 1.609,

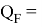
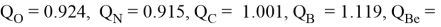
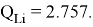
Полинг для фтора принял значение ЭО X(F) = 3.98. Выбранное нами значение равно X(F) = 3.99 эВ.

Для фиксирования ЭО фтора на значении 3.99 эВ был определен коэффициент, позволяющий осуществить переход суммарного потенциала к нормированному значению 3.99 эВ:

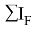
K = : n: X(F) = 413.685508 эВ:7:3.99 эВ = 14.81154854,

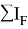
где K — коэффициент, который в дальнейшем используется для нормирования суммарных потенциалов ионизации химических элементов таблицы Менделеева.

Нормированное значение суммарного потенциала ионизации атома, для которого вычисляли его ЭО, определяли из выражения:

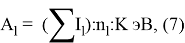
и, следовательно, ЭО химических элементов второго периода определяли из выражения:

X(l) =

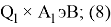
Х(F) = 1 413.685508:7:14.81154854 = 3.99 эВ;

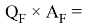
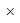
Х(O) = 0.924 335.9105401:6:14.81154854 = 3.49 эВ;

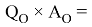
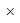
Х(N) =

0.915 242.3087757:5:14.81154854 = 3.00 эВ;

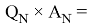
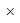
Х(C) = 1.001 148.0253:4:14.81154854 = 2.50 эВ;

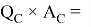
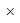
Х(B) = 1.199 71.38346:3:14.81154854 = 1.92 эВ;

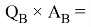
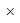
Х(Be) = 1.609 27.35384:2:14.81154854 = 1.48 эВ;

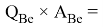
Х(Li) = 2.757 5.391719:1:14.81154854 = 1.0 эВ.

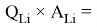
Необходимо отметить, что нормированные энергии ионизации для углерода и кремния точно совпадают со значениями их ЭО.

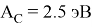
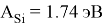
Детальный анализ проведенных вычислений позволил выявить выражение для расчета ЭО химических элементов второго периода. Действительно, перемножив выражения (6) и (7) и сократив подобные члены получим:

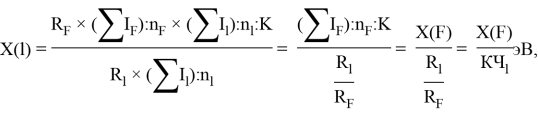
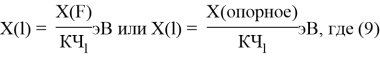
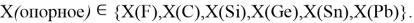
Сравнение полученных результатов, вычисленных с использованием различных радиусов [8, 9. 10], с результатами Полинга и Оллреда-Рохова [8] показало хорошее их совпадение (см. таблицу 1).

Таблица 1

Таблица электроотрицательностей для второго периода, рассчитанных по разным радиусам (ковалентные, металлические, расчетные) и разным методам

Элементы второго периода	X(l) Полинг [8]	X(l) О-Р [8]	X ( l ) расчет по эВ [ 10 ]	X ( l ) расчет по эВ [ 9 ]	X ( l ) расчет по эВ [8] Клементи
Li	1.00	0.97	0.977	0.975	1.00
Be	1.50	1.47	1.49	1.49	1.48
B	2.00	2.01	1.997	1.99	1.92
C	2.5	2.50	2.50	2.50	2.50
N	3.00	3.07	2.975	2.98	3.00
O	3.50	3.5	3.44	3.44	3.49
F	3.98	4.1	3.914	3.875	3.99

Расчет суммарных энергий ионизации для Si, Ge, Sn и Pb произведен на основе данных таблицы из [8] и электронной конфигурации для:

Si; Ge; Sn; Pb

, ,

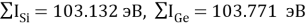
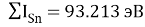
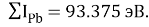
Исходные значения для расчета ЭО этих элементов вычислили путем деления нормированного суммарного значения потенциала ионизации на количество валентных электронов и на K = 14.81154854:

X(Si) = 103.13235:4:14.81154854=1.74 ;

(Ge) = 2 ;

(Sn) =93.21374:4:14.81154854=1.57 ;

Pb)=93.375:4:14.81154854=1.57 .

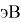
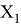
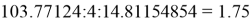
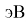
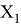
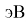
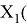
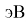
X(Si) = 1.74 эВ; (Ge) = 2 эВ; (Sn) =1.57 эВ; Pb)=1.57 эВ.

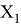
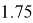
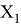
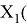
Как видно из таблицы Д. И. Менделеева химические элементы Ge, Sn и Pb (кроме Si) экранируются d-элементами, поэтому перерасчет их ЭО был осуществлен с помощью пропорций и использованием энергий ионизации:

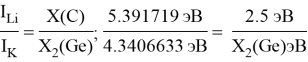
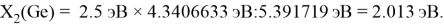
Полученные два значения для германия и позволяют вычислить коэффициент экранирования из отношения (коэффициент уменьшения величины ЭО):

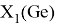
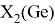
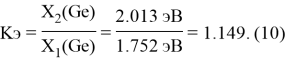
Олово и свинец также подвержены экранированию. Поэтому их значения ЭО определены аналогично — с помощью пропорций, включающих энергии ионизации и коэффициент Kэ:

(Sn)

(Pb) = 3.893905 эВ

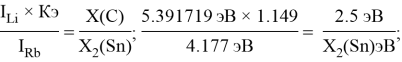
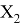
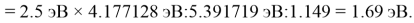
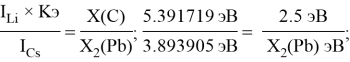
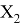
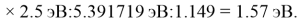
Для свободных атомов понятие радиус не имеет точного смысла. Однако, как следует из квантовых законов, размер атома ограничен снизу. Поэтому для расчета ЭО атомов переходных металлов использовались металлические радиусы, расчет которых связан с жесткими ограничениями формы и размеров кристаллических решеток. Кроме того, в качестве отправного был выбран шестой период, так как в нем f-электроны оказывают относительно слабое экранирующее действие. В результате чего валентные электроны атомов начиная с Hf стягиваются ближе к ядру, делая атомы компактными. Поэтому ошибка в определения размеров их радиусов меньше чем в четвертом и пятом периодах [2].

Расчет ЭО d-элементов шестого периода осуществлялся по формуле (8) с использованием данных о металлических радиусах из [9]. Результаты расчета приведены в таблице 2.

Для исключения в вычислениях погрешностей, связанных с малой точностью значений радиусов, ЭО элементов пятого и четвертого периодов, как и раньше, вычисляли в эВ с помощью пропорций (см. таблицу 2):

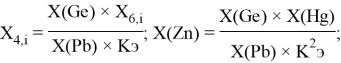
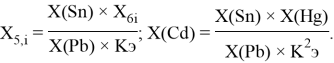
Таблица 2

Электроотрицательности d химических элементов в эВ

X(Sc)	X(Ti)	X(V)	X(Cr)	X(M)	X(Fe)	X(C)	X(N)	X(C)	X(Z)
1.12	1.44	1.52	1.57	1.63	1.69	1.74	1.75	1.80	1.65
X(Y)	X(Zr)	X(Nb)	X(Mo)	X(Tc)	X(Ru)	X(R)	X(P)	X(A)	X(C)
0.94	1.22	1.27	1.32	1.37	1.41	1.46	1.47	1.50	1.39
X(L)	X(H)	X(Ta)	X(W)	X(Re)	X(Os)	X(Ir)	X(Pt)	X(Au)	X(Hg)
0.998	1.29	1.34	1.41	1.46	1.51	1.56	1.57	1.61	1.70

Расчет ЭО sp-элементов четвертого, пятого и шестого периодов таблицы также осуществлялся с помощью пропорций. В качестве базового был выбран уже рассчитанный ранее второй период.

.

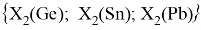
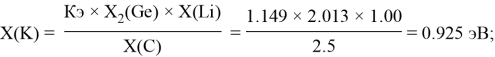
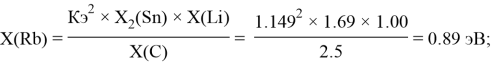
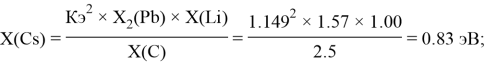
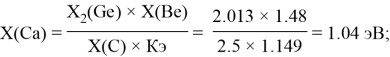
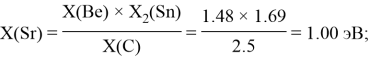
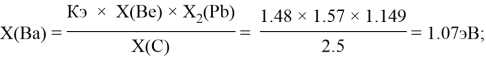
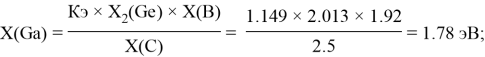
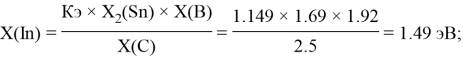
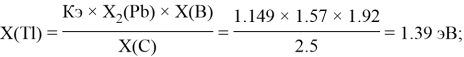
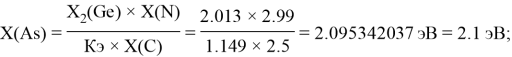
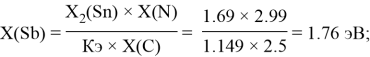
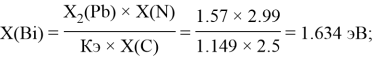
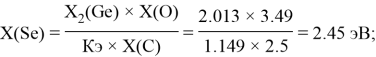
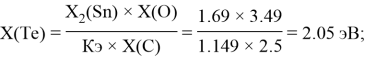
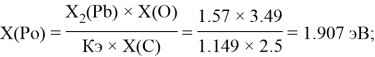
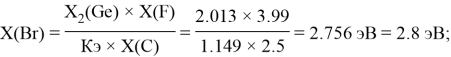
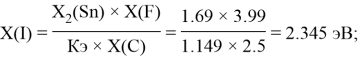
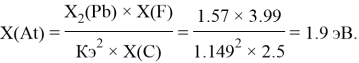
Полученные результаты сведены в таблицы 3 и 4.

Таблица 3

Обобщенные коэффициенты для вычисления ЭО

Таблица 4

Электроотрицательности sp химических элементов в эВ

	X ( l ) =X ( Na )
1.00 Li	1.01 Na
1.48 Be	1.21 Mg
1.92 B	1.45 Al
2 .5 C	1.74 Si
2.9 N	2.1 P
3.49 O	2.51 S
3.99 F	3.007 Cl

Для третьего периода значения ЭО атомов определили иным способом. Вычислили, с использованием различных наборов радиусов [9, 10], ЭО (Na) =1.084 эВ и (Na) = 1.016 эВ и нашли их среднее арифметическое значение:

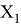
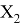
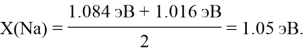
Полагая, что последовательность значений ЭО элементов третьего периода соответствует геометрической прогрессии, нашли ее знаменатель q. Для этого вычислили отношение значений X(Si) и X(Na) и извлекли из него кубический корень:

=1.2.

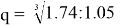
Первый член геометрической прогрессии определили путем последовательного деления на q = 1.2 значений ЭО, начиная с :

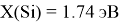
X(Al) = = 1.45 эВ; X(Mg) = X(Al):1.2 = 1.21 эВ;

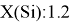
X(Na) = X(Mg): 1.2 = 1.01 эВ.

Приведенное ниже выражение позволило рассчитать значения ЭО в третьем периоде:

X(i) = X(Na) 11)

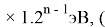
где n- количество валентных электронов искомого элемента.

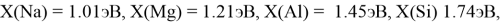
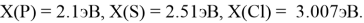
Расчет ЭО водорода отличен от изложенных выше. В качестве «опорного элемента» выбран гелий, ЭО которого относительно ЭО углерода была равна:

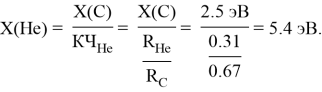
Непосредственный расчет ЭО водорода осуществлялся с помощью пропорции:

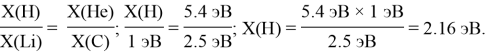
В данных вычислениях радиусы атомов рассчитанные Энрико Клементи.

Для оценки достоверности созданной в настоящем исследовании шкалы ЭО было осуществлено ее сравнение с приведенными в научной литературе другими общепризнанными шкалами ЭО. Полученные данные сведены в таблице 5.

Таблица 5

Сводная сравнительная таблица электроотрицательностей

№ п/п	Хим элем.	X ( l ) [4] Оганов	X(l) [6] Бацанов	X(l) [6] О-Р	X(l) [7] Кораб.	X(l) [8] О-Р	X(l) эВ Расчет	X(l) [8] Полинг
1	H	3.04	-	-	-	2.1	2.16	2.2
3	Li	2.17	0.92	0.88	0.86	0.97	1.00	0.98
4	Be	2.42	1.34	1.2	1.28	1.41	1.48	1.57
5	B	3.04	1.76	1.58	1.75	2.01	1.92	2.04
6	C	3.15	2.18	2.00	2.18	2.50	2.5	2.55
7	N	3.56	2.67	2.55	2.51	3.07	2.99	3.04
8	O	3.78	3.16	3.1	3.27	3.50	3.49	3.44
9	F	4.0	-	-	-	4.1	3.99	3.98
11	Na	2.15	0.98	0.93	0.92	1.01	1.01	0.93
12	Mg	2.39	1.22	1.09	1.22	1.23	1.21	1.31
13	Al	2.52	1.47	1.3	1.36	1.47	1.45	1.61
14	Si	2.82	1.68	1.43	1.55	1.74	1.74	1.91
15	P	3.16	1.92	1.66	1.83	2.06	2.1	2.19
16	S	3.44	2.17	1.88	2.2	2.44	2.51	2.58
17	Cl	3.50	-	-	-	2.83	3.007	3.16
19	K	2.07	0.83	0.86	0.77	0.91	0.925	0.82
20	Ca	2.20	0.99	0.98	1.08	1.04	1.04	1.00
21	Sc	2.35	1.14	1.12	1.24	1.20	1.1	1.36
22	Ti	2.23	1.27	1.26	1.35	1.32	1.44	1.54
23	V	2.08	1.41	1.42	1.4	1.45	1.52	1.63
24	Cr	2.12	1.44	1.48	1.5	1.56	1.57	1.66
25	Mn	2.2	1.6	1.63	1.66	1.60	1.63	1.55
26	Fe	2.32	1.68	1.72	1.71	1.64	1.69	1.83
27	Co	2.34	1.77	1.8	1.81	1.7	1.74	1.88
28	Ni	2.32	1.85	1.89	1.83	1.75	1.75	1.91
29	Cu	2.86	1.51	1.54	1.49	1.75	1.8	1.90
30	Zn	2.26	1.58	1.55	1.54	1.66	1.65	1.65
31	Ga	2.43	1.67	1.59	1.64	1.82	1.78	1.81
32	Ge	2.79	1.79	1.66	1.69	2.02	2.013	2.01
33	As	3.15	1.88	1.7	1.76	2.20	2.1	2.18
34	Se	3.37	2.14	2.01	2.15	2.48	2.45	2.55
35	Br	3.45	-	-	-	2.74	2.8	2.96
37	Rb	2.07	0.81	0.85	0.81	0.89	0.89	0.82
38	Sr	2.13	0.95	0.94	0.97	0.99	1.0	0.95
39	Y	2.52	1.17	1.11	1.19	1.11	0.93	1.22
40	Zr	2.05	1.30	1.25	1.22	1.22	1.21	1.33
41	Nb	2.59	1.37	1.34	1.41	1.23	1.27	1.6
42	Mo	2.47	1.48	1.46	1.54	1.3	1.32	2.16
43	Tc	2.82	1.56	1.55	1.66	1.36	1.37	2.10
44	Ru	2.68	1.65	1.63	1.64	1.42	1.41	2.2
45	Rh	2.65	1.72	1.69	1.68	1.45	1.46	2.28
46	Pd	2.70	1.76	1.71	1.77	1.35	1.47	2.20
47	Ag	2.88	1.51	1.46	1.47	1.42	1.52	1.93
48	Cd	2.36	1.57	1.46	1.57	1.46	1.38	1.69
49	In	2.29	1.64	1.47	1.68	1.49	1.49	1.78
50	Sn	2.68	1.74	1.54	1.79	1.72	1.69	1.96
51	Sb	3.05	1.83	1.57	1.67	1.82	1.8	2.05
52	Te	3.14	2.04	1.78	2.04	2.01	2.05	2.1
53	I	3.2	-	-	-	2.21	2.35	2.66
55	Cs	1.97	0.8	0.84	0.81	0.86	0.83	0.79
56	Ba	2.02	0.94	0.93	0.96	0.97	1.07	0.89
57	La	2.49	1.14	1.03	1.0	1.08	0.99	1.10
72	Hf	2.01	1.45	1.35	1.37	1.23	1.29	1.3
73	Ta	2.32	1.59	1.52	1.55	1.33	1.36	1.5
74	W	2.42	1.71	1.65	1.75	1.40	1.41	1.7
75	Re	2.59	1.8	1.74	1.77	1.46	1.46	1.9
76	Os	2.72	1.88	1.83	1.81	1.52	1.51	2.2
77	Ir	2.79	1.94	1.87	1.9	1.55	1.56	2.2
78	Pt	2.98	-	1.83	1.93	1.44	1.57	2.2
79	Au	2.81	1.66	1.58	1.55 1.64	1.42	1.61	2.4
80	Hg	2.92	-	1.53	1.54	1.44	1.695	1.9
81	Tl	2.26	1.75	1.53	1.68	1.44	1.39	1.8
82	Pb	2.62	1.8	1.53	1.86	1.55	1.57	1.8
83	Bi	2.69	1.86	1.54	1.61	1.67	1.63	1.9
84	Po	2 . 85	2.03	1.68	1.67	1.76	1.907	2.0
85	At	3.04	-	-	-	1.96	1.9	2.2

Выводы

По результатам проведенного исследования сформулированы следующие важные выводы:

— координационное число и нормированная величина суммарной энергии ионизации являются важными информативными параметрами химических элементов, а их совокупность, обусловленная зависимостями (5)-(9) — необходимой и достаточной для определения ЭО;

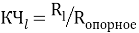
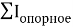
— точность вычисления ЭО в большей мере зависит от отношения рассчитанных по одной и той же методике радиусов катиона и аниона, а не от типов радиусов;

— расчет ЭО осуществляется по выражению (9), состоящем из двух «менделеевских чисел», либо методом пропорций;

— опорными электроотрицательностями в таблице Менделеева служат: ЭО углерода, кремния, германия, олова и свинца;

— при расчете ЭО водорода в качестве «опорного элемента» был выбран гелий;

— для sp-элементов второго и для d-элементов шестого периода прослеживается хорошо выраженная линейная зависимость между значениями ЭО атомов опорного периода и ЭО соответствующих им по порядку следования атомов в четвертом, пятом и шестом периодах;

— последовательность значений ЭО элементов третьего периода соответствует геометрической прогрессии, ее знаменатель q = 1.2;

— суммарная энергия ионизации электронов, находящихся на одном подуровне, равна среднему гармоническому их энергий ионизации;

— нормированные энергии ионизации для фтора =3.99А эВ, углерода эВ и кремния точно совпадают со значениями их ЭО.

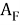
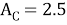
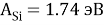
Результаты данного исследования будут использованы при создании принципиально нового метода расчета ЭО, существенно превосходящего по точности результаты Оллреда и Рохова.

Литература:

1. Бацанов С. С. Структурная химия. Факты и зависимости. М. МГУ, 2000. 292.
2. Еремин В. В., Борщевский А. Я. Основы общей и физической химии: Учебное пособие. Долгопрудный: Издательский Дом «Интеллект», 2018. — 848 с.
3. Черкасов А. Р., Галкин В. И., Зуева Е. М., Черкасов Р. А. Успехи химии, 67 (5) (1998). С. 423–441.
4. Tantardini, C., Oganov, A. R. Thermochemical electronegativinies of the elements. Nat Commun 12, 2087 (2021). https:// doi.org/10.1038/ s41467–021–22429–0.
5. Zahed Allahyari and Artem R. OganovThe Journal of Physical Chemistry C 2020 124 (43), 23867–23878DOI: 10.1021/acs.jpcc.0c07857)
6. Бацанов С. С., Звягина Р. А. Интегралы перекрывания и проблема эффективных зарядов. Новосибирск: Наука, 1966. 386.
7. Кораблев Г. А., Кодолов В. И., Заиков Г. Е. Оценка электроотрицательности через пространственно-энергетические характеристики атомов // Химическая физика и мезоскопия. Ижевск: ИПМ УрО РАН, 2009. Т. 11, № 1. С. 82–91.
8. Волков А. И., Жарский И. М. Справочник по общей и неорганической химии. — Минск: Букмастер, 2013. — 224 с.
9. Стась Н. Ф. Общая и неорганическая химия. Справочник: учебное пособие для среднего профессионального образования / — Москва: Издательство Юрайт, 2020. 92 с.
10. Годовиков А. А. Орбитальные радиусы и свойства элементов. /АН СССР Сибирское отделение. Труды института геологии и геофизики. Выпуск 337/-. Новосибирск: Наука, 1977. 157 с.