Одним из наиболее сложных разделов математики является решение текстовых задач. Как показывает практика, решение задач заключается не только в умении выполнять арифметические действия, но и знание формул, величин и их закономерности.
Умение решать задачи дает возможность человеку применять знания на практике, в повседневной жизни, раскрыть свои индивидуальные способности. При решении задач развивается наблюдательность, находчивость, абстрактное мышление.
Анализируя задачи сборника ОГЭ № 21 можно сказать, что для понимания сути задачи необходимы знания с 6-го по 9-й класс общеобразовательной школы. Решение задач сопровождается детальным анализом полученных величин, умением выражать неизвестные, правильностью отбора полученного ответа.
Ключевые слова: условие, вопрос, решение, ответ.
Для решения текстовых задач применяются три основных метода: арифметический, алгебраический и комбинированный.
1. Арифметический метод
- Составление условия задачи.
- Решение задачи.
- Выполнение проверки, отбор найденных значений по смыслу задачи для получения ответа.
2. Алгебраический метод
- Составление условия задачи.
- Составление уравнений, систем уравнений, неравенств, систем неравенств.
- Выполнение проверки решения.
3. Комбинированный метод
Этот метод включает в себя арифметический и алгебраический метод.
Алгоритм решения задач:
— Обозначить неизвестную величину через х .
— Выразить через нее другие величины.
— Найти зависимость между ними и на основании ее составить уравнение или систему уравнений.
— Решить уравнение или систему уравнений.
— Найти ответ на вопрос задачи, выполнив отбор решений по смыслу задачи.
— Проверить правильность решения задачи. Записать ответ.
Рекомендации при решении текстовых задач:
1. Если не получается определить зависимости величин, физических, химических, экономических терминов, законов, необходимо изучить тему, которая соответствует условию задачи.
2. При составлении уравнений, неравенств, систем уравнений правильно выбирать неизвестную величину. При возникновении затруднений заменить величину другой неизвестной.
3. При решении задачи не использовать ненужные величины.
4. При решении уравнений и систем уравнений применять рациональные методы решения.
5. Для успешного выполнения задания № 21 необходимо решить несколько подобных задач, самостоятельно составить обратные задачи и решить их .
Основные типы заданий № 21 в ОГЭ:
— Задачи на движение.
— Задачи на работу.
— Задачи на смеси и сплавы.
— Задачи на проценты.
Задачи на движение:
— Действие движения характеризуется тремя компонентами: пройденный путь, скорость и время.
Соотношение между ними:
— Путь = скорость • время
При движении по реке:
— Скорость по течению = собственная скорость транспорта + скорость течения реки
— Скорость против течения = собственная скорость транспорта — скорость течения реки
Задачи на работу:
Работу характеризуют три компонента действия:
— Время работы
— Объем работы
— Производительность (количество произведенной работы в единицу времени).
Соотношение между этими компонентами:
— Объем работы = время работы • производительность
Задачи на смеси и сплавы:
В задачах этого типа присутствуют три величины, соотношение между которыми позволяет составлять уравнение:
— Концентрация (доля чистого вещества в смеси);
— Количество чистого вещества в смеси (или сплаве);
— Масса смеси (сплава).
Соотношение между этими величинами следующее:
— Масса смеси • концентрация = количество чистого вещества
Задачи на проценты:
Решение задач на проценты сводится к основным трем действиям с процентами:
— нахождение процентов от числа;
— нахождение числа по его процентам;
— нахождение процентного отношения чисел.
Способы проверки решения задачи:
- Решение обратной задачи.
- Решение задачи другим способом.
Примеры решения задач:
- Первый велосипедист выехал из посёлка по шоссе со скоростью 12 км/ч. Через час после него со скоростью 10 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, в через 2 часа после этого догнал первого.
Решение:
Пусть х (км/ч) — скорость третьего велосипедиста. Скорость сближения третьего со вторым равна х-10 (км/ч). Значит третий догонит второго через 10/(х-10) часов. До выезда третьего велосипедиста первый уже ехал 1+1=2 часа и проехал 2•12=24 км, а второй ехал 1 час и проехал 10 км. Скорость сближения третьего с первым равна х-12 (км/ч) и он догонит его через 24/(х-12) часов. Зная, что третий догнал первого через 2 часа после того, как он догнал второго, составим уравнение:
24 - 10 =2
Х-12 х-10
24(х-10)-10(х-12) =2
(х-12)(х-10)
24х-240–10х+120 =2
х 2– 10х-12х+120
14х-120 =2
х 2– 22х+120
14х-120–2х 2 +44х-240=0
—2х 2 +58х-360=0 /-2
х 2– 29х+180=0
Д=(-29) 2– 4•1•180=121
Х1=9, не подходит по условию задачи
Х2=20
Ответ: 20 км/ч.
- Свежие фрукты содержат 79 % воды, а высушенные — 16 %. Сколько требуется свежих фруктов для приготовления 72 кг высушенных фруктов?
Решение:
В 72 кг высушенных фруктов воды 16 %, сухого вещества 100 %-16 %=84 %. Масса сухого вещества в 72 кг высушенных фруктов: 72•0,84=60,48 кг. Свежие фрукты содержат 79 % воды, а сухого вещества 100 %-79 %=21 %. Масса сухого вещества из свежих фруктов 60,48 кг и это 21 %, то 1 % равен 60,48: 21=2,88 кг. Свежих фруктов было 100 %, значит 2,88•100=288кг.
Ответ: 288 кг.
- Баржа прошла по течению реки 64 км и, повернув обратно, прошла ещё 48 км, затратив на весь путь 8 часов. Найдите собственную скорость баржи, если скорость течения реки равна 5 км / ч.
Решение:
Пусть х (км/ч)- собственная скорость баржи, тогда скорость баржи по течению реки х+5 (км/ч), против течения реки х-5 (км/ч).
Время=расстояние: скорость
По течению баржа плыла 64 часов, против течения 48 часов.
х+5 х-5
На весь путь затрачено 8 часов. Составим уравнение:
64 + 48 = 8 /:8
х+5 х-5
8 + 6 = 1
х+5 х-5
8(х-5)+6(х+5) = 1
(х+5)(х-5)
8х-40+6х+30 = 1
(х+5)(х-5)
14х-10 = 1
х 2– 25
14х-10-х 2 +25=0
—х 2 +14х+15=0
Д=14 2– 4•(-1)•15=256
Х1=-1, не подходит по условию задачи
Х2=15
Ответ: 15 км/ч.
- В сосуд, содержащий 7 литров 26-процентного водного раствора вещества, добавили 6 литров воды. Сколько процентов составляет концентрация получившегося раствора?
Решение:
В 7 литров раствора, содержащего 26 %=0,26вещества, добавили 6 литров воды, содержащей 0 %=0 вещества, получили раствор 7+6=13 литров. Концентрацию полученного раствора обозначим за х. Составим уравнение:
7•0,26+6•0=13х
7•0,26=13х
1,82=13х
х=1,82:13
х=0,14
0,14•100 %=14 %
Ответ: 14 %
- Первую половину пути автомобиль проехал со скоростью 34 км/ч, а вторую со скоростью 51 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Решение :
|
v |
t |
S |
|
|
1 |
34 |
S:34 |
S |
|
2 |
51 |
S:51 |
S |
|
1 +2 |
V среднее |
S:34+S:51 |
2S |
V среднее= 2 • S =40,8 км/ч
S + S
34 51
Ответ: 40,8 км/ч.
- Теплоход проходит по течению реки до пункта назначения 216 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 5 км/ч, стоянка длится 5 часов, а в пункт отправления теплоход возвращается через 23 часа после отплытия из него.
Решение:
Пусть х (км/ч)-скорость теплохода в неподвижной воде. Скорость теплохода по течению реки х+5 (км/ч), против течения реки х-5 (км/ч). Теплоход был в пути (без времени стоянки) 23–5=18 часов.
Время=расстояние: скорость
Время на путь по течению 216: (х+5), против течения 216: (х-5). Общее время в пути 18 часов. Составим уравнение:
216 + 216 = 18 /:18
х+5 х-5
12 + 12 =1
х+5 х-5
12•(х-5)+12•(х+5)-(х+5)(х-5) =0
х 2– 25
х 2– 24х-25 =0
х 2– 25
х 2– 24х-25 =0
Д=(-24) 2– 4•1•(-25)=676
х1=25
х2=-1, не подходит по условию задачи.
Ответ: 25 км/ч.
- Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 30 км/ч, а вторую половину пути проехал со скоростью, большей скорости первого на 9 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста.
Решение:
Пусть х (км/ч) скорость первого автомобилиста. Тогда на весь путь он потратил времени 1:х. Второй автомобилист проехал первую половину пути со скоростью 30 км/ч, а вторую половину пути со скоростью х+9(км/ч). Оба автомобилиста проехали одинаковое расстояние, обозначим его за 2.
На весь путь он затратил
1 + 1
30 х+9
В пункт они прибыли одновременно, значит время в пути одинаково. Составим уравнение:
2 = 1 + 1
х 30 (х+9)
60(х+9)-х(х+9)-30х =0
30х(х+9)
60х+540-х 2– 9х-30х =0
30х(х+9)
—х 2 +21х+540=0 /•(-1)
х 2– 21х-540=0
Д=(-21) 2– 4•1•(-540)=2601
х1=36
х2=-15, не подходит по условию задачи.
Ответ: 36 км/ч.
- Первый рабочий за час делает на 9 деталей больше, чем второй, и выполняет заказ, состоящий из 112 деталей, на 4 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
Решение:
Пусть х (дет/час)- производительность второго рабочего, тогда первый рабочий выполняет х+9 (дет/час). Первый рабочий выполняет 112 деталей быстрее, чем второй на 4 часа. Время работы второго рабочего 112: х, время работы первого рабочего 112:(х+9). Составим уравнение:
Производительность=работа: время
Время=работа: производительность
112–112 =4
х х+9
112(х+9)-112х=4х(х+9) /:4
28(х+9)-28х=х(х+9)
28х+252–28х=х 2 +9х
28х+252–28х-х 2– 9х=0
—х 2– 9х+252=0 /•(-1)
х 2 +9х-252=0
Д=9 2– 4•1•(-252)=1089
х1=12
х2=-12, не подходит по условию задачи.
Ответ: 12 деталей.
- Расстояние между пристанями А и В равно 45 км. Из А в В по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот проплыл 28 км. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 4 км/ч
Решение:
Пусть х(км/ч)- скорость лодки в неподвижной воде. Плот плыл со скоростью течения 4 км/ч, проплыл 28 км. Время движения плота 28:4= 7 часов. Лодка отправилась в путь позже, на 1 час. Значит в пути она была 7–1=6 часов. Скорость лодки по течению х+4 (км/ч), против течения х-4 (км/ч). Время, затраченное на путь по течению 45: (х+4), на путь против течения 45: (х-4). Всего в пути лодка была 6 часов. Составим уравнение:
45 + 45 =6
х+4 х-4
45(х-4)+45(х+4)-6(х+4)(х-4) =0
(х+4)(х-4)
45х-180+45х+180–6х 2 +96=0
—6х 2 +90х+96=0 /:(-6)
х 2– 15х-16=0
Д=(-15) 2– 4•1•(-16)=289
х1=16
х2=-1, не подходит по условию задачи.
Ответ: 16 км/ч.
- Велосипедист выехал с постоянной скоростью из городя А в город В, расстояние между которыми равно 209 км. На следующий день он отправился обратно в А увеличив скорость на 8 км/ч. По пути он сделал остановку на 8 часов, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А.
Решение:
Пусть скорость велосипедиста из В в А равна х (км/ч), Тогда скорость из А в В равна х-8 (км/ч). Время, которое затратил на дорогу из В в А равно 209: х (ч). Время, затраченное на дорогу из А в В, равно 209: (х-8) (ч).В задаче сказано, что велосипедист сделал остановку на 8 часов, при движении из В в А, время, затраченное из А в В и из В в А одинаковое. Составим уравнение:
209 + 8 = 209
х х-8
209х-1672+8х(х-8)-209х =0
х(х-8)
209х-1672+8х 2– 64х-209х=0
8х 2– 64х-1672=0 /:8
х 2– 8х-209=0
Д=64–4•1•(-209)=900
х1=19
х2=-11, не подходит по условию задачи.
Ответ: 19 км/ч.
- Два велосипедиста одновременно отправляются в 208-километровый пробег. Первый едет со скоростью на 3 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу первым.
Решение:
Пусть х (км/ч) скорость первого велосипедиста. Тогда скорость второго будет х-з (км/ч). Время, за которое первый велосипедист проходит 208 км равно 208:х (ч). Время, за которое проходит 208 км второй велосипедист 208(х-3) (ч). Разница во времени 3 часа. Составим уравнение:
208–208 =3
х-3 х
208х-208(х-3)=3х(х-3)
208х-208х+624–3х 2 +9х=0
—3х 2 +9х+624=0 /(-3)
х 2– 3х-208=0
Д=9–4•1•(-208)=841
х1=16
х2= -13, не подходит по условию задачи.
Ответ: 16 км/ч.
- Имеются два сосуда, содержащие 12 кг и 8 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 65 % кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 60 % кислоты. Сколько процентов кислоты содержится во втором растворе?
Пусть х %- концентрация первого раствора, у % -концентрация второго раствора. Величина кислоты в первом растворе 12х, во втором растворе 8у. Два раствора объединяют и получают 65 % раствор кислоты, значит величина кислоты в объединенном растворе будет 65(12+8). Составим уравнение:
12х+8у=65•20
При равных объемах растворов получается 60 % раствор кислоты, значит 1х+1у=60(1+1)
х+у=120
Составим систему уравнений:
Решение:
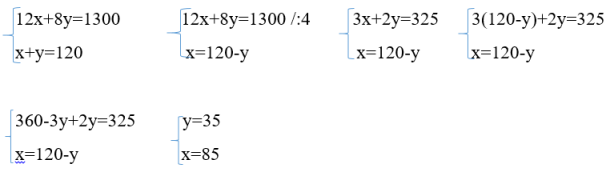
Значит во втором растворе 35 % кислоты.
Ответ:35 %.
- Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 51 минуту, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 251 км, скорость первого велосипедиста равна 10 км/ч. скорость второго- 20 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.
Решение:

Пока первый велосипедист стоял 51 минуту, второй со скоростью 20 км/ч проехал (51: 60) •20=17 км
За все остальное время два велосипедиста проехали: 251–17=234 км
Скорость сближения=скорость1+скорость2
Скорость сближения равна 10+20=30 км/ч.
Чтобы проехать эту часть пути, оба велосипедиста ехали: 234: 30=7,8 часа.
Второй проехал за 7,8 часа 7,8•20=156 км, всего второй проехал 156+17=173км.
Ответ: 173 км.
- Моторная лодка проплыла против течения реки 132 км и вернулась в пункт отправления, затратив на обратный путь на 5 часов меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 5 км/ч.
Решение:
Пусть х(км/ч)- скорость лодки в неподвижной воде. Тогда скорость лодки по течению х+5 (км/ч) против течения х-5 (км/ч).
Время= расстояние: скорость
Время движения по течению равна 132:(х+5) (ч), время движения против течения равна 132: (х-5) (ч). Обратный путь, по течению, лодка плыла на 5 часов меньше. Составим уравнение:
132–132 =5
х-5 х+5
132(х+5)-132(х-5)-5(х+5)(х-5) =0
(х-5)(х+5)
132х+660–132х+660–5х 2 +125=0
—5х 2 +1445=0 /:5
х 2 =289
х1=17
х2=-17, не подходит по условию задачи.
Ответ: 17 км/ч.
Задачи для самостоятельного решения:
- Первый велосипедист выехал из посёлка по шоссе со скоростью 24 км/ч. Через час после него со скоростью 21 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 9 часов после этого догнал первого.
- Свежие фрукты содержат 72 % воды, а высушенные — 26 %. Сколько сухих фруктов получится из 222 кг свежих фруктов?
- Баржа прошла по течению реки 48 км и, повернув обратно, прошла еще 42 км, затратив на весь путь 5 часов. Найдите собственную скорость баржи, если скорость течения реки равна 5 км/ч.
- Смешали 7 литров 25-процентного раствора вещества с 8 литрами 10-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
- Первые 105 км автомобиль ехал со скоростью 35 км/ч, следующие 120 км со скоростью 60 км/ч, а последние 500 км- со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
- Теплоход проходит по течению реки до пункта назначения 80 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 5 км/ч, стоянка длится 23 часа, а в пункт отправления теплоход возвращается через 35 часов после отплытия из него.
- Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 55 км/ч, я вторую половину пути проехал со скоростью, большей скорости первого на 6 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста.
- Первый рабочий за час делает на 6 деталей больше, чем второй, и выполняет заказ, состоящий из 140 деталей, на 3 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает первый рабочий?
- Расстояние между пристанями А и В равно 60 км. Из А в В по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в пункт А. К этому времени плот проплыл 30 км. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 5 км/ч.
- Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 112 км. На следующий день он отправился обратно в А, увеличив скорость на 9км/ч. По пути он сделал остановку на 4 часа,в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А.
- Два велосипедиста одновременно отправляются в 224-километровый пробег. Первый едет со скоростью на 2 км/ч большей, чем второй, и прибывает к финишу на 2 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.
- Имеются два сосуда, содержащие 30 кг и 42 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 40 % кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 37 % кислоты. Сколько процентов кислоты содержится во втором растворе?
- Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 28 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 286 км, скорость первого велосипедиста равна 10 км/ч, скорость второго — 30 км/ч. Определите расстояние от города, из которого выехал второй велосипедист до места встречи.
- Моторная лодка прошла против течения реки 208 км и вернулась в пункт отправления, затратив на обратный путь на 5 часов меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 5 км/ч.
- Первая труба пропускает на 15 литров воды в минуту меньше, чем вторая труба. Сколько литров воды в минуту пропускает первая труба, если резервуар объёмом 100 литров она заполняет на 6 минут дольше, чем вторая труба?
Литература:
1. Змаева Е. Решение задач на движение/ Математика. — 2000. — № 14
2. Талызина Н. Ф. Формирование общих приёмов решения арифметических задач/Формирование приёмов математического мышления — М.: ТОО «Вентана --Граф», 1995
3. «ОГЭ математика» под редакцией И. В. Ященко/36 вариантов/ Проект 2023/Национальное образование/Москва, 2022
4. Т.В Шклярова Как научить решать задачи/Грамотей/ 2016 г.
5. https://vpr-ege.ru/images/oge/21-oge-chekoldina.pdf
6. https://gdzotvet.ru/oge-ege/matematika/313-zadachi-iz-zadaniya-21-oge-po-matematike-fipi
7. https://math100.ru/oge-2021–21–1/
8. https://oge.sdamgia.ru/problem?id=406672
9. https://oge.sdamgia.ru/problem?id=630093
10. https://oge.sdamgia.ru/problem?id=3553302
11. https://urok.1sept.ru/articles/103564
12. https://studfile.net/preview/9463740/page:33/










