Исследование некоторых квадратурных формул Ньютона — Котеса в среде Maplesoft Maple 2022



Численные методы являются мощным инструментом вычислительной математики, использование которого позволяет решать многие математические, физические, экономические и технические задач. В данной статье излагается решение задачи численного интегрирования при помощи квадратурных формул Ньютона — Котеса, по средствам чего производится сравнение точности на примере некоторой функции.

Ключевые слова : интеграл, методы численного интегрирования, приближенное значение, точность.

Во все времена практика решения тех или иных прикладных задач демонстрировала недостаточность имеющихся в наличии аналитических методов математики и необходимость разработки численных методов. Приближенный характер результатов, полученными такими методами не являются принципиальным препятствием к их использованию в естественных и технических науках. Современные компьютеры за доли секунды выполняют огромное количество арифметических действий с многоразрядными числами, что обеспечивает требуемую точность результатов.

Интегральное исчисление является часто необходимой задачей, как в математике, так и в ряде пограничных с ней областях (экономика, радиотехника, теория управления и многое другое), решение которых сводятся к поиску определенных интегралов от таких функций, первообразные которых не выражаются через элементарные функции [3]. Кроме того, в приложениях приходится иметь дело с определенными интегралами, сами подынтегральные функции которых не являются элементарными. Это приводит нас к необходимости изучения приближенных методов вычисления определенных интегралов.

Теоретическое исследование

Итак, требуется вычислить определенный интеграл . С этой целью рассмотрим квадратурные формулы Ньютона-Котеса, к которым, в частности, относятся формулы прямоугольников, трапеций, парабол [1].

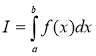
Метод прямоугольника

Разделим отрезок интегрирования на

одинаковых промежутков с пограничными точками (рис. 1). Шаг разбиения вычисляется согласно формуле и находим узлы из равенства

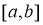
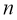
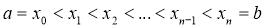
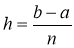
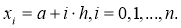
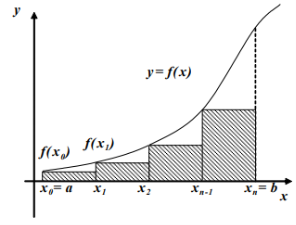
Рис. 1. Иллюстрация метода прямоугольников

Учитывая формулу площади прямоугольника и геометрический смысл определенного интеграла, получаем . Согласно свойству определенного интеграла (отрезок интегрирования можно разбивать на части), а именно , получаем где

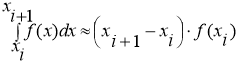
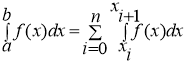
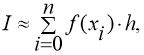
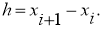
Метод трапеций

Разобьем отрезок интегрирования на равных промежутков длины узлами (рис. 2). Шаг разбиения определяем по формуле и узлы находим из равенства

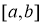
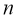
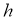
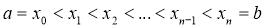
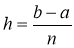
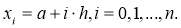
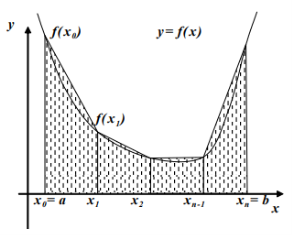
Рис. 2. Иллюстрация метода трапеций

Из курса основной школы известна теорема, согласно которой площадь трапеции находится как произведение полу суммы длин оснований на высоту. Следовательно, площадь криволинейной трапеции приблизительно равна площади трапеции с основаниями , и высотой , т. е. получаем . На основании свойства определенного интеграла очевидно, что . Таким образом, получаем следующую формулу

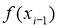
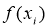
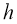
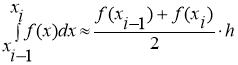
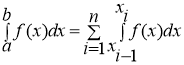
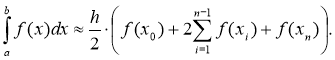
Метод Симпсона

Разобьем отрезок на

элементарных отрезков , , длины точками .(рис. 3). Пусть точки , являются серединами отрезков , соответственно. В таком случае узлы находятся по формуле

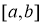
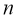
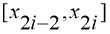
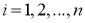
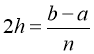
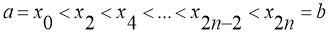
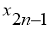
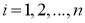
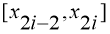
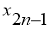
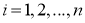
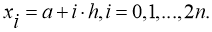
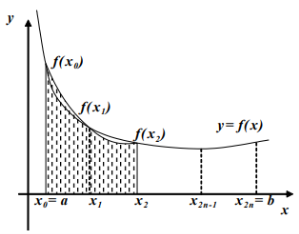
Рис. 3. Иллюстрация метода Симпсона

Суть метода Симпсона заключается, что на каждом промежутке подынтегральная функция приближается квадратичной функцией , проходящей через точки , ,

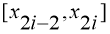
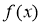
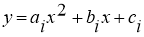
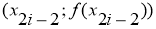
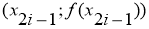
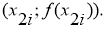
Следовательно,

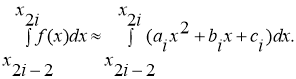
Поскольку, , , , то очевидно следующее равенство:

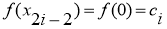
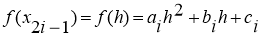
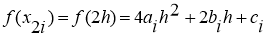
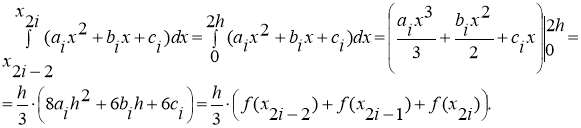
Таким образом, можно получить формулу Симпсона:

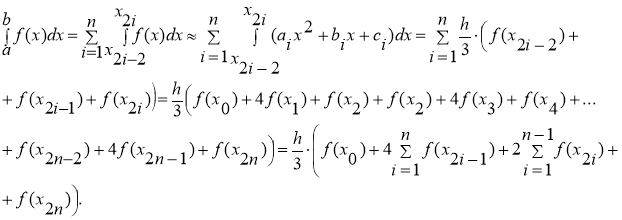
Практическая часть исследования

Постановка задачи: вычислить .

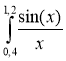
Решение: Для численного решения интеграла воспользуемся программным комплексом Maple 22 [2]. В соответствии с условием задачи исходными данными являются пределы интегрирования , и число разбиений .

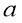
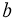
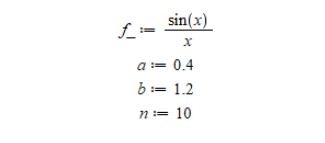
Работа в математическом пакете 𝑀𝑎𝑝𝑙𝑒 требует от исполнителя тонкости владения языка. К ним относится богатое разнообразие команд, функций и переменных.

Команда 𝑟𝑒𝑠𝑡𝑎𝑟𝑡 — производит отчистку листа 𝑀𝑎𝑝𝑙𝑒. Это означает, что все определенные для этого в программе переменные и другие объекты будут стерты. При этом программный код останется неизменным. Данная функция необходима для проведения компиляции. Переменная 𝐷𝑖𝑔𝑖𝑡𝑠 возвращает необходимое количество знаков после запятой. Установим точность вычисления 10 и проведем вычисление определенного интеграла при помощи встроенной функции int().

Приступим к программированию квадратурных формул. С этой целью зададим функцию при помощи встроенного конструктора unapply() . Рассчитаем длину промежутка , значения в узлах и значение подынтегральной функции .

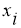
В соответствии с проведенным анализом методов интегрирования составим программный код.

Последний этап — анализ и сравнение результатов, полученных численными методами и при помощи встроенной функции int() (табл. 1).

Таблица 1

Анализ расчета и погрешность результатов

Способы расчета определенного интеграла			Относительная погрешность вычисления
Численные методы		Встроенная функция int()
Метод прямоугольников	0,7035976906	0,7115857343	0,0079880437
Метод трапеций	0,7114715553		0,0001141790
Метод Симпсона	0,7115857623		0,000000028

Анализируя последние результаты, мы можем сделать следующие выводы: во-первых, констатировать высокую точность вычисления определенного интеграла, что свидетельствует об адекватности разработанного программного кода, во-вторых, метод Симпсона является наиболее точным для решения поставленной задачи.

Заключение

В результате теоретического осмысления поставленной проблемы было установлено, что численные методы играют важную роль в вычислении определенных интегралов. Так, ценность данных методов, в которых используется ЭВМ, заключается в возможности вычислять интеграл для любой функции, что невозможно при интегрировании аналитическим методом.

В процессе практической части исследования выполнения были отработаны и закреплены практические навыки по разработке программы по вычислению определенного интеграла по квадратурным формулам Ньютона-Котеса (формулы прямоугольников, трапеций, парабол) в среде программирования Maplesoft Maple 2022.

Результаты, полученные в ходе исследования, можно использовать на уроках алгебры и начала анализа при изучении темы «Интегральное исчисление» в качестве дополнительного материала.

Литература:

1. Зенков А. В. Численные методы: учеб. пособие / А. В. Зенков. — Екатеринбург: Изд-во Урал. ун-та, 2016. — 124 с.
2. Малеко Е. М., Захаркина Е. И. Численные методы: учебное пособие / Е. М. Малеко, Е. И. Захаркина. Магнитогорск: Изд-во Магнитогорск. гос. техн. ун-та им. Г. И. Носова, 2012. — 60 с.
3. Масалова С. И. Исторические предпосылки становления дифференциального и интегрального исчисления // Известия высших учебных заведений. Северо-Кавказский регион. Серия: Естественные науки, 2006. — № 8. — С. 17–23.