Шестьдесят четыре клетки — черно-белая мозаика,
И воюют в этой сетке насмерть вороны и чайки;
В их блистательном сражении каждый ход звучит как нота.
Сочетает вдохновение мудрость и восторг полёта.
Шахматы — одна из самых древнейших игр с интересной историей, которая наполнена различными легендами. Для многих людей она является любимым увлечением. Достаточно многие занимаются шахматами профессионально, и игра становится неотъемлемой частью их жизни.
Шахматы — это не только увлекательная игра, но и оригинальный способ развития мышления, памяти, логики. Но главный феномен шахмат заключается в активном стимулировании нестандартного мышления. Подготовка ловушек и контрударов для соперника, сокрытие собственных планов игры и развитие каждый раз новой стратегии выступают отличным тренажером «думай-не-как-все».
Мы часто слышим, что между шахматами и математикой есть связь. Попробуем разобраться в этом и выясним, помогает ли умение играть в шахматы успешнее заниматься математикой?
Таким образом, выдвигаемые гипотезы звучат следующим образом:
- Между шахматами и математикой существует связь.
- Игра в шахматы положительно влияет на успеваемость по математике.
Исходя из выдвинутых гипотез, поставлена цель исследования: найти связь между шахматами и математикой и определить влияние игры в шахматы на успеваемость учеников по математике.
Задачи, которые решаем:
— познакомиться с историей шахмат, с шахматной доской и шахматными фигурами;
— кратко рассказать о правилах игры;
— назвать знаменитых людей, которые увлекались шахматами;
— ознакомиться с биографией знаменитых шахматистов и великих математиков;
— найти связь между шахматами и математикой и разобрать на примерах, в чем заключается эта связь;
— составить вопросы и провести опрос среди учеников гимназии и спортсменами шахматного клуба, чтобы понять влияние игры в шахматы на успеваемость по математике;
— проанализировать полученные результаты и сделать вывод.
Методы исследования:
- Анкетирование.
- Анализ литературных источников, материалов сети Интернет.
- Классификация, систематизация и обобщение полученных знаний.
Слово «шахматы» происходит из персидского языка от двух слов «шах» — «король» и «мат» — «мертв» — король (властитель) мертв.
Появилась эта игра примерно 2 000 лет назад в Индии. Называлась она первоначально не шахматы, а Чатуранга. В отличие от традиционных шахмат в нее одновременно играли 4 игрока, а ходы зависели от бросков игральных костей.
Название «чатуранга» переводится как «четырёхсоставная» и первоначально символизировало войско, которое в древней Индии состояло из колесниц, боевых слонов, конницы и пеших воинов. Игра изображало битву с участием четырёх родов войск, которыми руководил предводитель-раджа.
Со временим игра менялась, на смену чатуранге пришла игра шатрандж.
В IX–X веке игра попала в Европу, где были составлены «классические» правила игры. Окончательно правила игры в шахматы сформировались в XIX веке. В 1886 году был проведен первый чемпионат мира по шахматам.
Поскольку шахматы имеют такую древнюю историю, не удивительно, что с ними связаны разные предания и легенды, правдивость которых за давностью времени, проверить не представляется возможным.
Несколько интересных фактов о шахматах:
- После трех ходов с каждой стороны существует больше девяти миллионов возможных позиций.
- Самая длинная теоретически возможная шахматная партия — 5 949 ходов.
- Самая короткая шахматная партия называется дурацкий мат, состоящий из двух ходов: 1. f3 e5 и 2. g4 Qh4++. Ничья или проигрыш может также произойти и до того, как игроки начинают делать ходы, как в случае определенного сценария в турнирной таблице, так и в результате того, что игрок не пришел на игру.
Самая продолжительная по времени шахматная партия была сыграна между Иваном Николичем и Гораном Арсовичем в Белграде в 1989 году. Она длилась 20 часов 15 минут, за игру было сделано 269 ходов, и закончилась вничью.
- Складная шахматная доска была изобретена в 1125 году шахматным священником. Церковь в те времена запрещала священникам играть в шахматы, и поэтому он спрятал свою шахматную доску, сделав ее похожей на две книги, лежащие вместе.
- В Древней Индии в шахматы играли на пальцы. Побежденному отрубали палец на руке.
- Самый старый из сохранившихся наборов шахмат был найден на острове Льюис в Северной Шотландии. Он датируется XII веком нашей эры, и предположительно создан в Исландии или Норвегии. Его оригинальное исполнение послужило образцом для волшебных шахматных фигур в фильме «Гарри Поттер и философский камень».
- «Паламед» — так назывался первый в мире шахматный журнал. Выходил в столице Франции в Париже с 1636 по 1839 годы.
Шахматная партия играется между двумя партнерами — игроками, которые по очереди перемещают фигуры на квадратной доске, названной “шахматной”. Тот, кто имеет белые фигуры, начинает партию. Игрок получает право хода, когда его партнер сделал ход.
Цель каждого игрока является атака короля партнера таким образом, чтобы партнер не имел никаких возможных ходов, которые позволяют избежать «взятия» короля на следующем ходу. Об игроке, который достиг этой цели, говорят, что он поставил мат королю партнера и выиграл партию. Партнер, королю которого был поставлен мат, проиграл партию.
В игре в Шахматы задействовано две стороны, черные и белые, за каждую из которых выступает один игрок. Шахматная доска состоит из 64 клеток, светлых и темных, которые чередуются по цвету. Доска поделена на 8 столбцов и 8 рядов.
Столбцы имеют буквенное обозначение (слева направо: a, b, c, d, e, f, g и h), ряды — числовое (сверху вниз: 1, 2, 3, 4, 5, 6, 7 и 8). Таким образом, каждая клетка имеет обозначение -координаты, в зависимости от того, в каком столбце и каком ряду она находится. Сначала в записи клетки следует столбец, затем — ряд, например, клетка в левом нижнем углу имеет обозначение a1 (столбец a, ряд 1) (рис.1).

Рис. 1. Шахматная доска
Первоначальная позиция шахмат состоит из 16 белых фигур и 16 черных фигур, расположенных следующим образом (рис. 2)

Рис. 2. Расстановка шахматных фигур
Каждая шахматная фигура имеет определенную ценность (их измеряют в пешках, т. е. каждая фигура заменяет собой определенное количество пешек).
Ферзь стоит 9 очков, поэтому он гораздо ценнее, чем пешка, чья стоимость — всего 1 очко, конь стоит 3 пешки (рис. 3). Король в шахматах не оценивается — это самая главная фигура, и, если ему объявлен мат, игра проиграна.

Рис. 3. Ценность коня
Каждая фигура в шахматах двигается по-своему:
Пешка может двигаться лишь по одной клетке за раз, за исключением своего первого хода (при первом ходе у пешки есть выбор — сходить сразу на две клетки, если ей ничего не мешает), или на одну клетку. Пешки перемещаются только прямо вперед, и не могут ходить назад (пешка — единственная шахматная фигура, которая не имеет права ходить назад).
Ладья ходит по вертикали и горизонтали на любое количество полей.
Слон ходит по диагонали на любое количество полей.
Король самая важная фигура на шахматной доске и в тоже время очень слабая. Король может ходить всего лишь на одно поле вокруг себя.
Ферзь самая сильная и значимая фигура на шахматной доске. Он может ходить и как ладья и как слон.
Конь в шахматах ходит в форме буквы «Г» в любом направлении.
Многие великие полководцы были умелыми игроками в шахматы.
Маршал Советского Союза Конев говорил: «Если считать шахматы игрой, то нет ей равной среди игр по тренировке памяти и логике мышления, по воспитанию выдержки, силы воли и других ценных качеств человеческого характера».
Шахматы любили и любят многие знаменитые люди прошлого и современности — короли, государственные деятели, военачальники, ученые, писатели и музыканты.
Итальянский ученый Галилео Галилей очень любил шахматы. Игра Галилия — свободная, со сложными комбинациями. Галилео любил играть «вслепую» — не глядя на доску. Он в уме создавал различные шахматные комбинации и обдумывал стратегию партии. В шахматы Галилео играл до конца свой жизни — 77 лет. И только в 76 начал жаловаться на память — ему стало тяжело удерживать в уме партию целиком.
Большими любителями шахмат были отец Петра I — Алексей Михайлович — и дед — Михаил Федорович. В Оружейной палате хранится комплект — серебряная шахматная доска с металлическими фигурами, посеребренными и раскрашенными. Комплект принадлежал деду Петра. С детства увлекался шахматами и Петр. В XVI веке церковь запретила шахматы. Став царем, он отменил данный запрет и старался ввести среди придворных моду на эту игру. Приказал на ассамблеях отводить специальные комнаты и уголки для шахматистов.
Наполеон начал играть в юности. Шахматы всегда были с ним — в военных походах, плаваниях и даже в светских салонах. Он играл в перерывах между сражениями.
Большим поклонником шахмат был А. Пушкин. Играть он научился еще в лицее. Поэт одним из первых в России понял значение шахмат для семьи. Он обучил игре Наталью Николаевну. Современники отмечали, что она была одной из лучших шахматисток Петербурга.
Толстой играл в шахматы с юности. Предположительно, его обучил старший брат. Он играл даже во время обороны Севастополя. В Париже и Ясной Поляне Л. Толстой играл с И. С. Тургеневым.
Профессор химии Д. Менделеев не только хорошо играл в шахматы, но и приобщил к ним коллег. Организовал шахматный кружок на химическом факультете Петербуржского университета. Менделеев всегда переживал за результат партии, поэтому никогда не участвовал в соревнованиях. Он несколько раз играл с М. И. Чигориным (первым русским шахматистом — претендентом на титул чемпиона мира) и один раз даже обыграл его.
Эйнштейн увлекся шахматами довольно поздно — уже после создания теории относительности. Его привлекала осмысленность шахматного мира, которой не было в окружающей действительности.
Понятие симметрии имеет очень важное значение при рассмотрении объектов живой и неживой природы. Нахождение элементов и признаков симметрии важно при изучении таких классических фундаментальных наук как: математика, физика, химия м других.
Некоторые случаи симметрии мы можем наблюдать и в процессе игры в шахматы. В первую очередь шахматисты говорят о естественной симметрии, которая возникает в ходе шахматной партии. Еще один случай симметрии в шахматах это применяемый для решения этюдов и шахматных задач.
Можно выделить два наиболее распространенных вида симметрии:
— Осевая;
— Центральная.
Прямая разделяет шахматное поле на левый и правый фланги (граница между вертикалями «d» и «e») при осевой симметрии или же прямая разделит доску на верхнюю и и нижнюю части (по границе четвертой и пятой горизонтали) (рис.4).
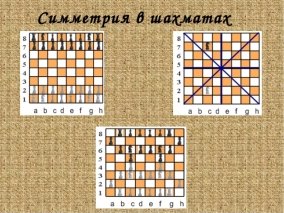
Рис. 4. Симметрия в шахматах
Если, белый конь стоит на с2, а черный на с7 (рис. 5), то мы говорим, что эти кони расположены симметрично. Осями являются и большие диагонали.

Рис. 5. Симметричное расположение коней на шахматной доске
Симметрией обладает исходное расположение шахматных фигур. В истории известна такая интересная история. В шахматный клуб пришел человек с заявлением, что он нашел способ игры в шахматы черными фигурами не проигрывая. «И что это за способ?» — спросили его. «Элементарно, — ответил гость, нужно повторять ходы за соперником!» Проверить теорию шахматного изобретателя решил С. Ллойд, который в итоге и поставил ему мат в 4 хода. Сейчас уже неизвестно как Ллойд сделал это. Я же могу показать, как поставить мат за 6 ходов в подобной ситуации.
1) с2-с3 с7-с6
2) е2-е3 е7-е6
3) Кg1-е2 Кg8-е7
4) Кb1-с3 Кb8с6
5) Кс3-е4 Кс6-е5
6) Ке4-d6х
Все мы конечно же посещали театры или цирк. Там нам приходится использовать билет, в котором определено твое место в зале. В билете указан номер ряда и номер места в ряду.
Описание того, где расположен тот или иной объект (предмет, место), называют его координатами. Так на билете номер ряда и номер места в ряду — координаты этого места.
Более чем за 100 лет до н. э. греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести хорошо теперь известные географические координаты: широту и долготу — и обозначить их числами.
В ХIV в. Французский математик Н. Оресм ввел, по аналогии с географическими, координаты на плоскости. Он предложил покрыть плоскость прямоугольной сеткой и называть широтой и долготой то, что мы теперь называем абсциссой и ординатой. Это нововведение оказалось чрезвычайно продуктивным. На его основе возник метод координат, связавший геометрию с алгеброй. Основная заслуга в создании метода координат принадлежит французскому математику Р. Декарту и называется Декартовой системой координат на плоскости.
А причем здесь шахматы? На шахматной доске тоже есть координаты. При профессиональной игре, обычно, ведут записи (обозначение фигур и координаты этих фигур).
На рисунке 6 мы видим, некий алгоритм определения координат чёрного короля.

Рис. 6. Определение координат шахматных фигур
Система координат используется не только в шахматах, но и в других играх, например, морской бой и других.
Число — одно из основных понятий математики, позволяющее выразить результаты счета или измерения. Со временем люди научились не только называть числа, но и обозначать их цифрами (условные знаки для обозначения чисел).
Из признака делимости на 2 следует, что натуральные числа, которые делятся на 2, называются четными, остальные — нечетными.
На шахматной доске так же есть чётность и нечётность. Тут они связаны с номером хода.
При каждом ходе король меняет четность хода. Например, первый ход — нечётный, второй — чётный и т. д. (рис. 7).
Чётность, нечётность на шахматной доске ещё раз подтверждают прямое отношение шахмат к математике.
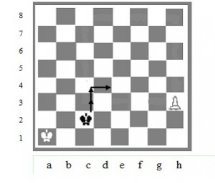
Рис. 7. Четность и нечетность на шахматной доске
Можно сказать, что ничего удивительного и интересного здесь нет. Можно подумать, что при виде шахматной доски мы сразу вспоминаем геометрию (из-за геометрические формы доски). Это, безусловно, так, но геометрическая форма ещё не всё.
Дело в том, что при игре в шахматы, как и в любой другой науке, есть свои определённые правила. И существует такое правило, как «правило квадрата».
Квадратом называется прямоугольник, у которого все стороны равны. При этой композиции (рис. 8) неопытные шахматисты рассуждают так: пешка идет сюда, король туда, пешка сюда, король туда и т. д. и при этом они часто путаются и, в конце концов, просчитываются.
Однако исход партии легко оценить при помощи «правила квадрата». Достаточно выяснить, может ли король при своем ходе попасть в квадрат пешки. Итак, в нашей композиции черные при ходе делают ничью (попадают в квадрат), а при ходе противника проигрывают.
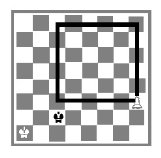
Рис. 8. Правило квадрата
Существует гипотеза о том, что шахматы произошли из так называемых магических квадратов.
Магический квадрат представляет собой квадратную таблицу n×n, заполненную целыми числами и обладающую следующим свойством: сумма чисел каждой строки, каждого столбца, а также двух главных диагоналей одна и та же. Для магических квадратов порядка 8 она равна 260 (см.рис.9). Закономерность расположения чисел в магических квадратах придает им волшебную силу искусства.
Рассмотрим одну из старинных дебютных табий (начальных расположений фигур) под названием альмуджаннах. Она получается из современной расстановки при помощи следующих симметричных ходов белых и черных: 1. d3 d6 2. e3 e6 3. b3 b6 4. g3 g6 5. c3 c6 6. f3 f6 7. c4 c5 8. f4 f5 9. Кc3 Кc6 10. Кf3 Кf6 11. Лb1 Лb8 12. Лg1 Лg8.
Подсчитав сумму чисел, стоящих на восьми полях— d2, d3, e2, e3, d6, d7, e6, e7, участвующих в первые двух ходах, мы неожиданно получим магическое числе 260. Тот же результат даст и каждая последующая пара приведенных ходов. Подобные примеры и позволяют высказать гипотезу о связи магических квадратов с шахматами.

Рис. 9. Альмуджаннах и магический квадрат
Примеры решения шахматных и математических задач приведены в приложении 1.
Мир шахмат не ограничивается только игрой в шахматы, даже если включить сюда все правила и приемы игры, историю соревнований, десятки и сотни имён гроссмейстеров и чемпионов, и т. д. Существует один из популярных жанров занимательной математики, к которому относятся математические игры, задачи и развлечения на шахматной доске. Этот жанр называется шахматной математикой. Многие математики занимались решением задач на шахматной доске. Рассмотрим конкретные примеры.
Леона́рд Э́йлер— швейцарский, немецкий и российский математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук.
Леонард Эйлер родился 4 апреля 1707года в г. Базель (Швейцария), а умер в Санкт-Петербурге в возрасте 76 лет.
Он занимался математической задачей на шахматной доске о ходе коня.
Старинная задача о ходе шахматного коня:
Требуется обойти конем все 64 клетки шахматной доски так, чтобы на каждой клетке конь был только один раз и затем возвратился бы в клетку, из которой вышел.
Метод Эйлера состоит в том, что сначала конь двигается по произвольному маршруту, пока не исчерпает все возможные ходы. Затем оставшиеся не пройдёнными клетки добавляются в сделанный маршрут, после специальной перестановки его элементов.
Карл Фридрих Гаусс (1777–1855) — немецкий математик, астроном, геодезист и физик, иностранный член-корреспондент (1802) и иностранный почетный член (1824) Петербургской АН. Гауус был удостоен почетного титула «принц математиков».
Внимание Карла Гаусса привлекла задача о восьми ферзях: сколькими способами можно расставить на доске восемь ферзей так, чтобы они не угрожали друг другу, т. е. никакие два не стояли на одной вертикали, горизонтали и диагонали?
Больше восьми мирных ферзей (как и ладей) на обычной доске расставить невозможно. Найти какое-нибудь расположение восьми ферзей, не угрожающих друг другу, легко (на рис.10 представлены четыре искомые расстановки). Значительно труднее подсчитать общее число расстановок, в чем, собственно, и состоит задача. Гаусс, в свою очередь, нашел 72 решения этой задачи.
Позднее было доказано, что их существует 92.

Рис. 10. Задача о восьми ферзях
Также многие математики решали и решают головоломки на шахматной доске.
Почти в каждом сборнике олимпиадных математических задач или книгах с головоломками можно найти красивые и остроумные задачи с участием шахматной доски и фигур. Многие из них имеют интересную историю, привлекали к себе внимание известных ученых.
Шахматная математика — один из самых популярных жанров занимательной математики, логических игр и развлечений.
Игра в шахматы требует устойчивого внимания, терпения, логического мышления, способности планировать и предвидеть последствия действий на несколько ходов вперед. Чтобы хорошо играть в шахматы, нужна определенная точность в восприятии предоставленной информации, способность сконцентрироваться и построить план своих действий, внося в него изменения по ходу игры. Эти же функции когнитивной сферы задействуются при решении математических задач.
Данная связь раскрывает новые возможности для развития способностей школьников. Регулярная умственная практика в игровом режиме позволит детям не только лучше справляться с заданиями по математике, но и приведет к развитию мышления в целом. Таким образом, занятия шахматами — даже недолгий курс — могут быть полезным инструментом в развитии математических способностей детей.
Таким образом, игра в шахматы положительно влияет на успеваемость по математике.
Для более точного исследования данного предположения я решил узнать у учеников гимназии, играют ли они в шахматы и как относятся к математике. Для этого разработал вопросы анкеты и провёл опрос. В опросе участвовало 60 человек. Это ученики 2 и 7 классов нашей гимназии. Учащиеся отвечали на следующие вопросы:
- На сколько хорошо Вы знакомы с игрой в шахматы?
- Хотелось бы Вам научиться играть в шахматы / повысить уровень (тем, кто умеет играть)?
- Почему полезно играть в шахматы?
- Могут ли люди разных языков, культур и воззрений играть друг с другом по универсальным правилам шахмат?
- Как Вы считает нужен ли шахматный кружок в школе?
- Помогает ли умение играть в шахматы легче изучать математику?
- Любите ли Вы математику?
- Для чего нужно учить математику?
- Чем привлекает наука математика?
- Какие оценки у Вас преобладают по математике?
Проведя анкетирование, было выяснено, что многие ученики гимназии знают и любят игру в шахматы. Большинство из них хотят повысить свой уровень, так как считают игру полезной и считают, что именно занятия шахматами помогают разобраться им в сложной и интересной науке математике. Также гимназисты считают, что шахматисты хорошо знают математику и математики являются хорошими шахматистами.
Из 60 опрошенных гимназистов 52 считают необходимым наличие шахматного кружка в гимназии.
Также обнаружена взаимосвязь между успеваемостью по математике и умением играть в шахматы. Гимназисты, которые ответили, что не умеют играть в шахматы, также ответили, что не любят математику и основной бал по математике у них 3 или 4. И наоборот, абсолютное большинство учеников, играющих в шахматы, имеют высокую успеваемость по математике с преобладанием 4 и 5 баллов.
И игра в шахматы, и занятие математикой учат мыслить, думать, принимать решения. Только, к сожалению, для некоторых шахматы — это игра, приносящая удовольствие, а занятие математикой — лишь необходимость.
Изучив историю шахмат, познакомившись с биографией некоторых математиков и шахматистов, мы можем сделать вывод о том, что математика и шахматы тесно связаны между собой. Эта связь обусловлена тем, что шахматы — одна из наиболее удобных моделей, используемых математиками при решении той или иной задачи.
Играя в шахматы, мы приобретаем много полезных качеств, тренируем память, учимся упорству, находчивости, развиваем фантазию. Занятие шахматами способствует развитию математических способностей человека.
Шахматы — это и вид интеллектуальной борьбы, и соревнование, а любое соревнование совершенствует сильные черты личности.
Таким образом, математика помогает шахматистам играть и выигрывать. А шахматы в свою очередь помогают нам решать простейшие и даже самые сложные математические задачи, помогают развивать логику, внимание и таким образом знать математику на пять.
Приложение 1
Задачи шахматные и математические
Задачи на четность, нечётность
- Конь вышел на поле А8 и через несколько ходов вернулся на него.
Докажите, что он сделал четное число ходов.
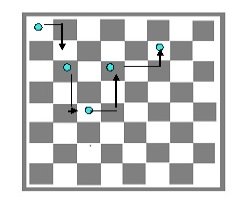
Рис. 11. Решение задачи 1
Решение:
Вы, наверное, заметили, что, делая каждый ход, конь меняет цвет клетки, на которой он стоит. Следовательно, каждый нечетный ход конь будет вставать на чёрную клетку. Исходя из этого и зная то, что конь должен вернуться на клетку А8, белого цвета, мы можем сказать, что он вернется через четное число ходов.
- Может ли конь пройти с поля a8 на поле h1, побывав по дороге на каждом из остальных полей ровно один раз?
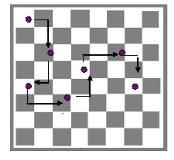
Рис. 12. Решение задачи 2
Решение: Как и в предыдущем задании, при каждом ходе конь меняет цвет клетки, на которой он стоит. Следовательно, на доске 63 хода (нечетное число), а8 — белая клетка, при 63 ходе конь будет на чёрной клетке.
Задача на разделение шахматной доски
Из шахматной доски 8*8 вырезали две противоположные угловые клетки. Докажите, что остаток доски нельзя разделить на доминошки (прямоугольники 1*2).
Решение:
Так выглядит доминошка. На шахматной доске, при удалении двух угловых клеток (а это либо две белых, либо две чёрных клетки), у нас получится 30 чёрных (белых) и 32 белых (чёрных). А это значит, что мы не сможем разделить оставшуюся часть доски на доминошки (так как неравное количество чёрных и белых клеток).

Рис. 13. Решение задачи 3
Задача на расстановку фигур
Расставьте на обычной шахматной доске три ферзя и две ладьи одного цвета так, чтобы все остальные поля доски оказались под боем.
Решений этой задачи достаточно много, одно из них приведено на рисунке 14.

Рис. 14. Решение задачи 4
Мат в центре доски
На доске стоит белый король (поле A1), и чёрный король (поле D4) (Рис. 15). Добавьте две белые ладьи и белого коня так, чтобы чёрный король оказался заматован.

Рис. 15. Условие задачи 5
Решение этой задачи приведено на рисунке 16.
.

Рис. 16. Решение задачи 5
Литература:
- Е. Я. Гик Шахматы и математика. — М., Наука, 1983
- М. Гарднер Математические чудеса и тайны — М., Наука, 1978
- Е. И. Игнатьев В царстве смекалки — М., Наука, 1984.
- С. Лойд Математическая мозаика — М., Мир, 1984.
- А. П. Савин Энциклопедический словарь юного математика — М.,
- Савин А. Математические миниатюры. М.: Детская литература, 1991.
- http://chessok.net
- http://www.telesmi.info
- wikipedia.org
- https://livrezon.com/publication/polezno-li-unym-matematikam-igrat-v-shahmaty











