В статье автор проводит изучение такого объекта как треугольник Рело. Изучаются различные варианты его построения и способы его использования в реальном мире.
Ключевые слова: треугольник Рело, циркуль, геометрия.
Цель исследовательской работы: изучить способы построения треугольника Рело и области его применения.
Актуальность. Исторически геометрия начиналась с треугольника, поэтому треугольник — символ геометрии. Геометрия треугольника дает возможность почувствовать красоту математики. В современном мире при быстро развивающихся технологиях нельзя обойти фигуру постоянной ширины — треугольника Рело.
Треугольник Рёло, или «круглый треугольник», — плоская выпуклая геометрическая фигура, представляющая собой область пересечения трёх равных кругов с центрами в вершинах правильного треугольника и радиусами, равными его стороне. Негладкая замкнутая кривая, ограничивающая эту фигуру, также называется треугольником Рёло.
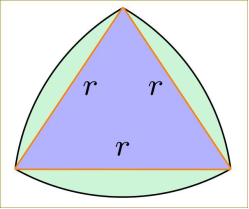
Рис. 1. Треугольник Рело
Треугольник Рело можно построить 2 способами:
1-й способ: используя правильный треугольник (с помощью циркуля и линейки).
— На каждой стороне треугольника строится дуга окружности с радиусом соразмерным длине стороны;
— область пересечения трёх равных кругов с центрами в вершинах правильного треугольника и радиусами, равными его стороне образуют треугольник Рело;
— негладкая замкнутая кривая, ограничивающая эту фигуру, также называется треугольником Рёло (рис. 2) [1].
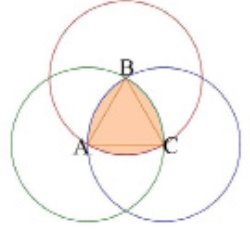
Рис. 2. Первый способ построения треугольника Рело
2-й способ: с помощью одного только циркуля.
— Последовательно строятся три равных окружности;
— центр первой выбирается произвольно;
— центром второй может быть любая точка первой окружности
— центром третьей — любая из двух точек пересечения первых двух окружностей (рис. 3).
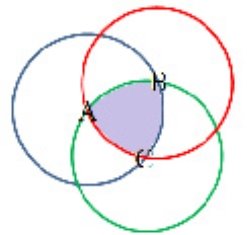
Рис. 3. Второй способ построения треугольника Рело
Разберем сферы применения:
— Строительство/Архитектура
В форме треугольника Рёло сделаны канализационные люки в различных городах. Сам люк выполнен в форме треугольника Рело, а крышка в форме обычного треугольника. За счёт этого, как бы крышку не поворачивали, она никогда не сможет провалиться в люк (рис. 4).

Рис. 4. Люк в форме треугольника Рело
Также треугольник Рело используется в архитектуре, а именно конструкция из двух его дуг образует характерную для готического стиля стрельчатую арку.
— Музыка
В форме треугольника Рело выполнен медиатор или плектр для игры на струнах щипковых инструментов (рис. 5)

Рис. 5. Плектр
— Механика
Треугольник Рело используется в кулачковых механизмах [2], в грейферных механизмах [3], в двигателях [4], а также в швейных машинах и даже в часовых механизмах [5].
Итак, мною были изучены принципы построения треугольника Рело, а также было найдено огромное количество способов его применения в нашей жизни.
Литература:
- Соколов Д. Д. Постоянной ширины кривая // Математическая энциклопедия / Гл. ред. И. М. Виноградов. — М.: Советская энциклопедия, 1984. — Т. 4. — С. 519. — 608 с.
- Математические этюды Круглый треугольник Рело // www.etudes.ru
- Берже М. Геометрия / Пер. с франц. Ю. Н. Сударева, А. В. Пажитнова, С. В. Чмутова. — М.: Мир, 1984. — Т. 1. — С. 529–531. -560 с.
- Двигатель Ванкеля / Редкол.: А. Ю. Ишлинский (гл. ред.) и др.. — 3–е изд., перераб. и доп. — М.: Советская энциклопедия, 1989. — С. 72. — 656 с
- Гопей И. A. Мои часы. — М.: Часовая литература, 2010. — № 1. — С. 39.










