К настоящему времени найдено огромное количество свойств вписанного четырёхугольника и конструкций, с ним связанных, причём многие из них регулярно появляются при решении задач с различных математических олимпиад. К сожалению, большинство этих свойств описано в разрозненных источниках, что создаёт проблему при подготовке к олимпиадам математического цикла, поэтому своей задачей автор поставил их поиск и систематизацию, а также нахождение новых.
В данной статье собраны и систематизированы темы и методы доказательств, связанные со вписанным четырёхугольником, а для более качественного погружения в тему предложены 15 подробно разобранных задач олимпиадного уровня, 4 из которых были придуманы в процессе работы над статьёй.
Автором были найдены свойства 11 и 12, а также изящные доказательства ко многим другим.
Некоторые обозначения:
— ABCD — сам вписанный четырёхугольник
— AC ∩ BD = P, AB ∩ DС = E, BC ∩ AD = F
— — описанная окружность ABCD, O — её центр, R — радиус
— M — точка Микеля ABCD
— H — ортоцентр ABCD
— M XY — середина XY
— O XYZ — центр описанной окружности треугольника XYZ
— H XYZ — ортоцентр XYZ
— (XYZ) — описанная окружность XYZ
— Простые задачи и темы
— Углублённые задачи и темы
— Продвинутые задачи и темы
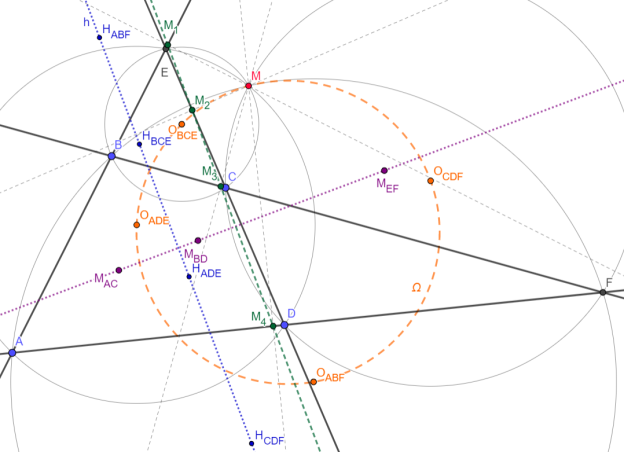
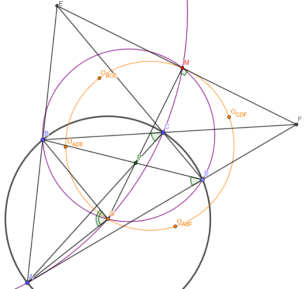
Общие сведения о полном четырёхстороннике
— Полным четырёхсторонником называется фигура (ABCDEF), образованная четырьмя прямыми общего положения
— (BCE), (ADE), (CDF), (ABF) пересекаются в одной точке M, называемой точкой Микеля четырёхугольника ABCD (доказательство элементарно; M же является центром поворотной гомотетии, переводящей AB в DC и BC в AD, подробнее — см. [1] или [4])
— H BCE , H ADE , H CDF , H ABF лежат на одной прямой, называемой прямой Обера (здесь и далее h), и M AC , M BD , M EF также лежат на одной прямой, прямой Гаусса, причем прямая Гаусса h (доказательство через радикальные оси см., например, [3], про радикальные оси см., например, [1])
— O BCE , O ADE , O CDF , O ABF и M лежат на одной окружности (здесь и далее )
Доказательство:
1) Поскольку M лежит на каждой из (BCE), (ADE), (CDF), (ABF), то, из свойств прямой Симсона (подробнее см., например, [1]) M 1 — M 2 — M 3 , M 1 — M 2 — M 4 , M 1 — M 3 — M 4 и M 2 — M 3 — M 4 , где
M 1 , M 2 , M 3 , M 4 — основания перпендикуляров из M на AB, CD, BC и AD соответственно, откуда
M 1 — M 2 — M 3 — M 4 (отсюда, кстати, также следует коллинеарность H BCE , H ADE , H CDF , H ABF как лежащих на совпадающий прямых Штейнера M относительно (BCE), (ADE), (CDF), (ABF) (св-во прямой Симсона))
2) Т.к, M лежит на каждой из (BCE), (ADE), (CDF), (ABF), то при инверсии в M (св-ва инверсии см. [3]) O BCE , O ADE , O CDF , O ABF перейдут в точки O BCE ’, O ADE ’, O CDF ’, O ABF ’, являющиеся отражениями M относительно сторон образа ABCD, значит O BCE ’, O ADE ’, O CDF ’, O ABF ’, как и M 1 , M 2 , M 3 , M 4 будут лежать на одной прямой, а значит до инверсии O BCE , O ADE , O CDF , O ABF и M лежали на одной окружности, ч.т.д.
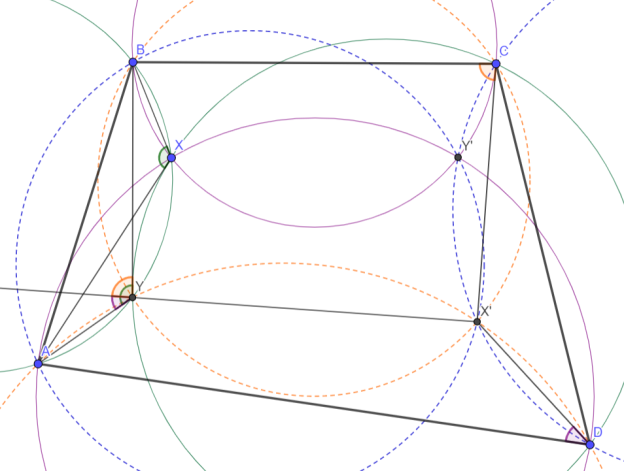
Сопряжение Клоусона и инверсия Микеля
— Дан четырёхугольник ABCD и точка X, (ABX) ∩ (CDX) = Y, (BCX) ∩ (ADX) = Y’, тогда (ADY), (BCY), (ABY’) и (CDY’) пересекаются в одной точке X’, называемой сопряженной Клоусона точки X в четырёхугольнике ABCD.
Доказательство:
1) После инверсии в X задача становится равносильной существованию точки Микеля полного четырёхсторонника
Следствие: AXB = X’CB + X’DA (следует из вписанности BXYA, BCX’Y и ADX’Y) для точки X’, удовлетворяющей равенству AXB = X’CB + X’DA и аналогичным относительно других сторон (признак сопряжения точек по Клоусону), верно, что она есть сопряженная Клоусона точки X в ABCD. Кроме того, если у X есть изогонально сопряженная точка в ABCD, то она совпадает с X’. (Подробнее про изогональное сопряжение см., например, [2])
— Из свойств поворотной гомотетии следует, что для полного четырёхсторонника ABCDEF
— MA * MC = MB * MD = ME * MF и AMC, BMD и EMF имеют общую биссектрису l.
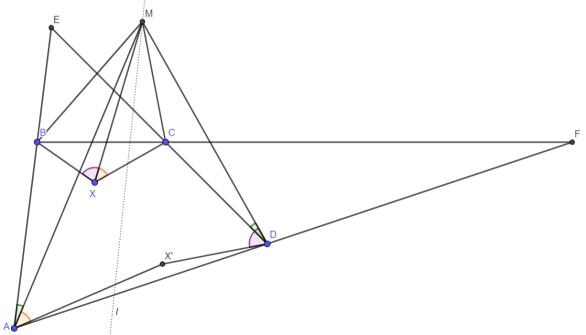
Тогда для преобразования i
M
, являющегося композицией инверсии в M с радиусом
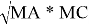
Утверждение: пусть i M : X X’, тогда X’ будет сопряженной Клоусона для X в четырёхугольнике ABCD
Доказательство:
1) Из свойств инверсии имеем MXC = MAX’ и MXB = MDX’, а из свойств поворотной гомотетии BAM = CDM, откуда BXC = BAX’ + X’DC. Получая аналогичные равенства для других сторон, заключаем, что X и X’ — сопряженные Клоусона по признаку, ч.т.д.
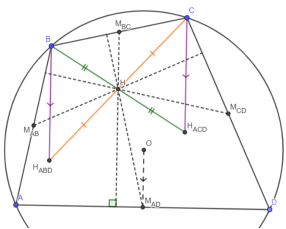
Высоты и диагонали во вписанном четырёхугольнике
— Лемма Монжа: высоты, опущенные из середин сторон ABCD на противоположные стороны, пересекаются в одной точке (ортоцентре ABCD), причем эта точка делит пополам каждый из отрезков, соединяющих вершины с ортоцентрами “противоположных” треугольников
Доказательство:
1) Поскольку H ABD H ACD CB — параллелограмм (свойство 1) то BH ACD и CH ABD , равно как BH ACD , AH BCD и CH ABD , DH ABC точкой пересечения делятся пополам, значит, все четыре отрезка (AH BCD , BH ACD , CH ABD и DH ABC ) пересекаются в одной точке (H) и делятся ей пополам
2) Т. к. H ABD H ACD CB — п-мм, то высота из M BC на AD, параллельная BH ACD , будет проходить через его точку пересечения диагоналей.
Аналогично другие высоты будут проходить через точки пересечения диагоналей соответствующих п-ммов, которые, как мы поняли, совпадают (точка H), ч.т.д.
3*) Кроме того, H ABD H ACD H ABD H ABC центрально симметричен ABCD
4*) Если рассматривать ломаную ACBD (а не ABCD) как “основную”, то тогда её сторонами будут являться AC и BD H перпендикулярам из середин AC и BD на BD и AC соответственно
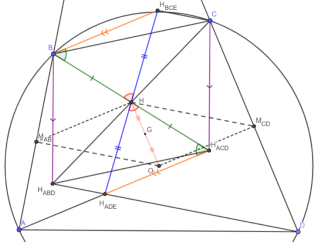
— H есть середина H BCE H ADE и H ABF H CDF
Доказательство:
1)H ADE H ACD || BH BCE , H ADE H ACD = BH BCE , HB = H ACD HH ADE H ACD = HBH BCE H ADE HH ACD = BHH BCE и HH BCE = HH ADE H — середина H BCE H ADE , аналогично H — середина H ABF H CDF , ч.т.д.
Следствие: H ADE H CDF = H ABF H BCE
— G — середина OH, где G — центр масс ABCD
Доказательство:
1)M AB H || OM CD и HM CD || M AB O M AB HM CD O — п-мм по признаку G, середина M AB M CD , есть и середина OH, ч.т.д.
— P h
Доказательство:
1)Поскольку h есть радикальная ось окружностей, построенных на AC и BD как на диаметрах, то принадлежность P прямой h равносильна равенству степеней P относительно этих окружностей, что, в свою очередь, равносильно PA * PC = PB * PD
Прямая Эйлера вписанного многоугольника
— У любого вписанного многоугольника существует ортоцентр
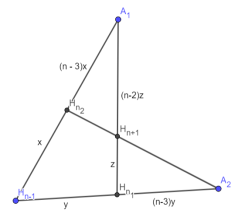
Если во вписанном n-угольнике соединить каждую вершину с ортоцентром (n-1)-угольника, образованного оставшимися вершинами, то все полученные отрезки пересекутся в одной точке и поделятся в отношении (n — 3):1, считая от вершины. Докажем это по индукции:
- База для n = 4 доказана
- Пусть утверждение верно для n-угольника
- 1) Рассмотрим 2 вершины A 1 и A 2 (n+1)-уг., ортоцентр H n -1 (n-1)-уг., вершинами которого являются оставшиеся n-1 вершина, тогда ортоцентр H n _1 n-уг., не содержащего A 1 — такая точка на A 2 H n -1 , что A 2 H n _1 /H n _1 H n -1 = (n — 3):1, аналогично и H n _2 .
2) Пусть A 1 H n _1 ∩ A 2 H n _2 = H n +1 , тогда из теоремы Менелая для A 1 H n -1 H n _1 : A 1 H n +1 /H n +1 H n _1 = (n-2):1
3) Аналогично любые 2 отрезка A i H n _ i и A k H n _ k точкой пересечения поделятся в отношении (n-2):1, считая от вершины все такие отрезки пересекутся в одной точке и поделятся в отношении (n-2):1
- Предположение верно для всех n, ч.т.д.
— В любом вписанном многоугольнике центр описанной окружности, центр масс и ортоцентр лежат на одной прямой, причем центр масс делит отрезок соединяющий центр описанной окружности с ортоцентром в отношении (n-2):2, считая от центра описанной окружности
Про геометрию масс, в частности про центр масс, можно прочитать в [6], нам же понадобится только то, что центр масс n-угольника с равными весами в вершинах — точка на отрезке, соединяющим произвольную вершину с центром масс оставшихся (n-1) вершин, делящая его в отношении (n-1):1, считая от вершины (по сути, это точка, при подвесе за которую многоугольник останется в равновесии. В частности, на отрезке это будет действовать правило рычага, а если рассматривать четырёхугольник с равными массами в вершинах, то это будет центр четырёхугольника Вариньона)
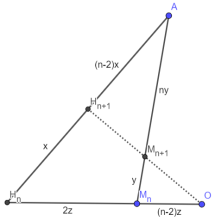
Итак, докажем исходное утверждение по индукции:
- База для n = 3 общеизвестна
- Пусть предположение верно для n-угольника
- 1) Рассмотрим вершину A вписанного (n+1)-уг., центр его описанной окружности O, его центр масс M n +1 и ортоцентр H n +1 , а также центр масс M n и ортоцентр H n n-угольника, образованного из данного “выкидыванием” A, тогда:
2) Используя доказанные свойства ортоцентра, определение центра масс и индуктивное предположение, получаем, что
AH n +1 /H n +1 H n = (n — 2):1, AM n +1 /M n +1 M n = n:1 и OM n /M n H n = (n — 2):2. По теореме Менелая для AH n M n легко проверить, что H n +1 , M n + 1 и O лежат на одной прямой (эта прямая называется прямой Эйлера вписанного n-угольника), а из теоремы Менелая для OH n +1 H n получаем, что OM n +1 /M n +1 H n +1 = (n — 1):2 4. Предположение верно для всех n, ч.т.д
Исследуем вписанный четырёхугольник
— Свойство 4: M EF
(EMC + CMF = ABC + CDA = )
— Свойство 5: O — P — M
Действительно, т. к. O — точка велосипедистов* для (CDF) и (ABF), то OO CDF FO ABF — п-мм, а OMO CDF O ABF — трапеция, но O CDF O ABF EF, т. к. является серпером к MF OM EF, п по т. Брокара OP EF O — P — M, ч.т.д.
Здесь еще можно отметить, что
O BCE O ADE O ABF O CDF , O BCE O ADE OM, O CDF O ABF OM — равнобокие трапеции и OO ADE EO BCE — п-мм
*про точку велосипедистов можно почитать в [2] или [4]
— Свойство 6: O и P — сопряженные Клоусона (по признаку)
— Свойство 7: AOCM и BODM — вписанные
Действительно, т. к. при инверсии Микеля O P, A C, B D и A — P — C, B — P — D, то до инверсии AOCM и BODM были вписанными, ч.т.д.
— Свойство 8: O
— Свойство 9: h есть радикальная ось и
Доказательство:
1) После инверсии Микеля центры описанных окружностей перейдут в точки симметричные M относительно сторон ABCD, то попадут на прямую Штейнера точки M для каждой из описанных окружностей, т. е. на прямую Обера, а перейдет в себя точки пересечения и перейдут в точки пересечения и h, но, поскольку после инверсии Микеля “конфигурация” не изменилась, то значит эти точки останутся на месте, т. е. они лежат и на , и на , и на h
h — радикальная ость и , ч.т.д.
2) Т. к. после инверсии Микеля переходит в h, а O в P, h, то до инверсии O , ч.т.д.
Следствие: пусть ∩ EF вторично в V, тогда, т. к. OV будет являться линией центров и , и h m, то OV || m
— Свойство 10: O ADE H ADE O BCE H BCE и O CDF H ABF O ABF H CDF вписаны в концентрические окружности
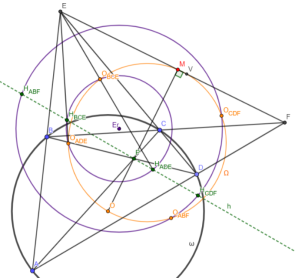
Доказательство:
1)Т. к. AED BEC, то, первое, BEH BCE = CEH ABE , который, очевидно, = AEO ADE E — H BCE — O ADE , аналогично E — O BCE — H ADE , и второе, EO ADE / EO BCE = EH ADE / EH BCE EO ADE * EH BCE = EO BCE * EH ADE
O ADE H ADE O BCE H BCE — вписанный по признаку, аналогично и O CDF H ABF O ABF H CDF
2) Т. к. O BCE O ADE O ABF O CDF — равнобокая трапеция, то серпер к O BCE O ADE совпадает с серпером к O ABF O CDE ;
т. к. H ADE H CDF = H ABF H BCE , то серпер к H ABF H CDF совпадает с серпером к H BCE H ADE центры описанных окружностей O ADE H ADE O BCE H BCE и O CDF H ABF O ABF H CDF совпадают, ч.т.д.
Их общий центр называется точкой Эрвея
— Свойство 11: прямые Обера ломаных ABCD, ACBD и ACDB пересекаются в одной точке.
Действительно, в разделе “Высоты и диагонали во вписанном четырёхугольнике” мы поняли, что этой ортоцентр ABCD является также и ортоцентром ACBD, аналогично и ACDB лежит на каждой из прямых Обера.
— Свойство 12: окружности ломаных ABCD, ACBD и ACDB соосны.
Поскольку радикальной осью каждой из окружностей является соответственная прямая Обера, то, в силу свойства 11, H имеет равную степень относительно каждой из этих окружностей (и ) для этих трёх окружностей нашлось 2 точки с равными относительно них степенями (вторая — O, её степень относительно каждой — 0, причём нетрудно проверить, что O и H совпадают только если ABCD — квадрат), а значит у них есть общая радикальная ось, ч.т.д.
Следствие: центры окружностей ломаных ABCD, ACBD и ACDB лежат на одной прямой
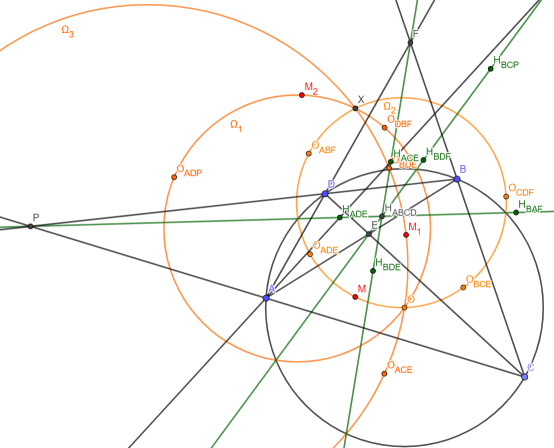
Для лучшего понимания рассуждений про ломаные на чертеже “по порядку” идут A — D — B — C вместо A — B — C — D
Задачи
- (Iran TST, 2022, Problem 4) Диагонали вписанного в окружность с центром O четырёхугольника ABCD пересекаются в точке P. Точки M и N — середины сторон AD и BC соответственно. Описанные окружность BCP и MON пересекаются в точке F (не на дуге MN), аналогично ADP и MON пересекаются в E. Докажите, что OE = OF.
Решение:
1) Пусть E 1 и F 1 (на чертеже — E и F) — точки пересечения PN с (ADP) и MP с (BPC), покажем, для начала, что это и есть E и F
2) Поскольку PN — медиана BCP, то для ADP это будет симедиана (про них можно почитать в [4] или [5]), значит, E 1 APD — гармонический четырёхугольник (см [3] или [6]), аналогично и F 1 BPC E 1 MPF 1 = (из свойств гармонических четырёхугольников) 2AMP = (из подобия) 2CNB = E 1 NF 1 ;
MIN = DAC — ADP = ME 1 N E 1 MNF 1 I — вписанный, O (MIN) E = E 1 , F = F 1
3) Пусть FP ∩ (APD) = Y, тогда, в силу равенств DY = EA, OD = OA, EAO = YDO, YDO = EAO OY = OE
4) Заметим, что O — точка велосипедистов для (ADP) и (BCP) OY = OF OE = OF, ч.т.д.
5) Можно также отметить, что (BCP) и (ADP) вторично пересекаются на (MON) (EXF = EMF, где X — как раз вторая точка пересечения (BCP) и (ADP))
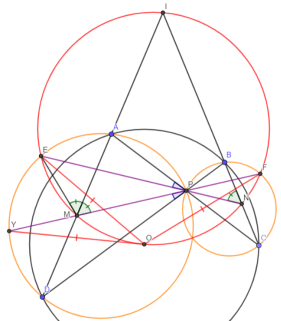
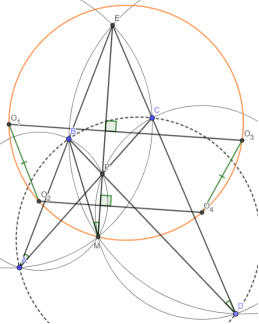
- (Автор) Диагонали четырёхугольника ABCD пересекаются в точке P, прямые AB и CD — в Е. Оказалось, что расстояние между центрами описанные окружностей треугольников ABP и ACE равно расстоянию между центрами описанных окружностей треугольников CDP и BDE. Докажите, что ABCD — вписанный
Решение:
1) Используя ранее доказанный факт про полный четырёхсторонник, примененный для ломаной ACDB, заключаем, что O 1 O 2 O 3 O 4 — вписанный, где O i -центр одной из окружностей (см чертёж)
2) В силу O 1 O 2 = O 3 O 4 , O 1 O 2 O 4 O 3 — трапеция O 1 O 3 || O 2 O 4 , но O 1 O 3 — срединный перпендикуляр к EM, где M — точка Микеля ломаной ACDB, а O 2 O 4 — к PM EM и PM или || или совпадают, но у них есть общая точка M совпадают E — P — M BAP = BME = BDE ABCD — вписанный по признаку, ч.т.д.
- Даны точки A, B и C, лежащие на одной прямой и точка P, на этой прямой не лежащая. Докажите, что P и центры описанных окружностей треугольников APB, APC и BPC лежат на одной окружности.
Решение:
1) Поскольку основания перпендикуляров, опущенных из P на стороны треугольника, образованного данными центрами описанных окружностей есть середины PA, PB и PC, т. е. точки, лежащие на одной прямой, то по “обратной” прямой Симсона нужный нам четырёхугольник вписанный, ч.т.д.
- (IMO 1992, Problem 5) Во вписанном четырёхугольнике ABCD отметили такую точку X, что CAB = DAX и BCA = XCD. Докажите, что XB = XD
Решение:
1) Рассмотрим X’, изогонально сопряженную к точке X, тогда X’ AC и BX’A + CX’D = BX’C = CX’D
2) Поскольку изогональю к радиусу является высота, то угол между DX и DO = углу между DG и DX’, который равен углу между BX’ и BE (=

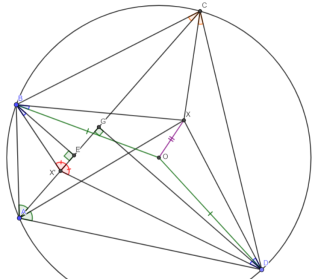
- (Автор) Диагонали вписанного четырёхугольника ABCD пересекаются в точке P, прямые AB и CD — в E, AD и BC — в F. Пусть X 1 — середина отрезка, соединяющего проекции E на AC и BD, Y 1 — E на AD и BC, X 2 — F на AC и BD, Y 2 — F на AB и CD, X 3 — P на AB и CD, Y 3 — P на AD и BC. Докажите, что X 1 Y 1 , X 2 Y 2 , X 3 Y 3 пересекаются в одной точке.
Решение:
Секрет задачи заключается в следующем факте: пусть K, L, M и N — проекции точки P пересечения диагоналей вписанного четырёхугольника ABCD. Тогда прямая Гаусса KLMN совпадает с прямой Обера ABCD. Тогда на каждой из прямых Гаусса (X 1 Y 1 , X 2 Y 2 , X 3 Y 3 для соответствующей ломаной) будет лежать ортоцентр ABCD эти 3 прямые ∩ в одной точке, ч.т.д.
Докажем этот факт:
1) Пусть Z’ — проекция Z, AB (CD), на CD (AB), X — середина KM, Y — KK’ ∩ MM’
2) Мы уже показали, что P H
ADE
H
BCE
принадлежность X H
ADE
H
BCE
равносильна принадлежности Y этой прямой (P — X — Y). Докажем, что Y H
ADE
H
BCE
с
помощью проверки равенства отношений проекций H
BCE
H
ADE
и H
BCE
Y
на AB и CD (т. е. покажем
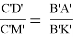
3) Пусть AED = , тогда
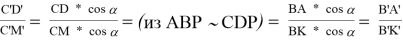
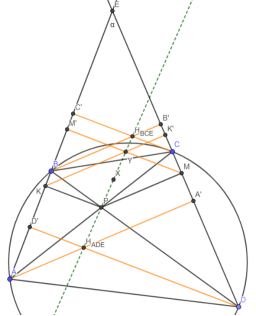
- (Автор) Диагонали вписанного четырёхугольника ABCD пересекаются в точке P, прямые AB и CD — в E. Точки M и N таковы, что MP CD, ME BD, NP AB и NE AC. Докажите, что AMDN — параллелограмм.
Доказательство:
Для решения нам понадобится следующая лемма: пусть дан вписанный четырёхугольник ABCD, P — точка ∩ его диагоналей, E — прямых AB и CD. Пусть Q и L — проекции E и P на AC и CD соответственно, а O — середина AD. Тогда Q, L и O лежат на одной прямой.
1) Рассмотрим T и K — проекции E и P на BD и AB соотв., тогда, очевидно, TKPLQE — вписанный в окружность с диаметром EP и TQLK — трапеция в силу LEQ =
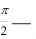
2) Пусть BAC = . Рассмотрим h =
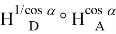
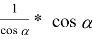
3) Пусть TK ∩ QL = O 1 , тогда, очевидно из п.1 O 1 L = O 1 K, кроме того, по теореме Паскаля для KTPQLE, A, O 1 и D лежат на одной прямой. Но на прямой AD есть только одна точка, равноудалённая от K и L O = O 1 Q — L — O
Итак, вернемся к задаче:
1) К обозначениям точек в лемме добавим PK ∩ EM = F и PL ∩ EN = G
2) Очевидно, что F и G — ортоцентры EBP и ECP соотв. EFN = — EBP = — ECP = EGP MFGN — вписанный
3) Применим лемму для ABCD и MFGN: точка O пересечения TK и QL является как серединой AD, так и серединой MN AMDN — п-мм по признаку, ч.т.д.
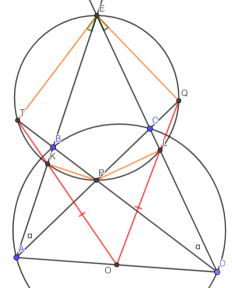
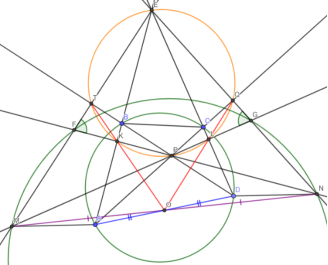
- (Автор) Диагонали вписанного четырёхугольника ABCD пересекаются в точке P. Пусть K и L — проекции P на AB и CD соответственно. M — середина AD. KC и BL пересекаются в точке X, прямые PX и KM — в Y. Докажите, что YPLD — вписанный.
Решение:
1) Пусть AB ∩ CD = E, N — проекция E на AC.
2) Воспользуемся леммой из предыдущей задачи: K, L и N коллинеарны YLD = NLE = (из вписанности PLNE) CPE.
3) Заметим, что CPL = BPK по лемме об изогоналях (подробнее — см [7]) для вершины P и точек K, B, C, L: CPE = XPB
4) YPD = EPN = YLD YPLD — вписанный, ч.т.д.
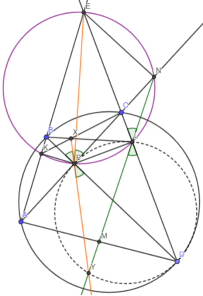
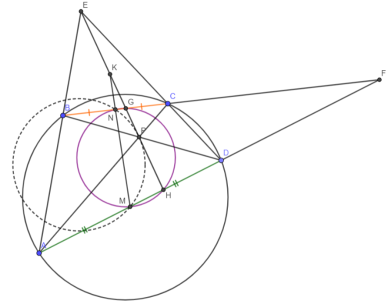
- (СПбМО, 2009, задача 7) Дан вписанный четырёхугольник ABCD. Его диагонали пересекаются в точке P, а продолжения сторон AB и ВС — в точке E. M и N — середины AD и BC соответственно. Докажите, что описанная окружность треугольника PMN касается EP.
Решение:
1) Пусть BC ∩ AD = F, EP ∩ BC = G, EP ∩ AD = H, K — середина EP
2) Известно, что четвёрки [B; C; G; F], [A; D; H; F] и [E; P; Q; H] — гармонические (это верно для произвольного ABCD, про гармонические четвёрки см. [4] или [5]) из св-в гармонических четвёрок, т. к. M, N, K — середины AD, BC и EP соответственно, KP 2 = KG * KH (1), FG * FN = FC * FB, FH * FN = FD * DA, но FD * FA = FC * FB FG * FN = FH * FM GNMH — вписанный
3) K, N, M лежат на одной прямой как середины диагоналей полного четырёхсторонника, образованного BECP (его прямая Гаусса) из вписанности GNMH и равенства (1), KP 2 = KN * KM, откуда KP, т. е. EP, касается (PMN) по признаку, ч.т.д.
Задачи для самостоятельного решения
- (Автор) Во вписанном четырёхугольнике ABCD DB AC и BA = 25, BD = 63, BC = 39. Найти радиус описанной окружности.
- На окружности с диаметром AC выбрали точки B и D, E и F — проекции A и C на BD. Докажите, что BE = CF.
- (Теорема Помпею) Точка P лежит на меньшей дуге AB описанной окружности равностороннего треугольника ABC. Докажите, что PC = PA + PB.
- Пусть P лежит на меньшей дуге AB описанной окружности равнобедренного треугольника ABC (AC = CB). D — основание перпендикуляра из C на PB. Докажите, что PA + PB = 2PD.
- (Е. А. Емельянов) Докажите, что точки пересечения окружностей с центрами в серединах дуг AB, BC, CD, DA окружности и проходящие через A, B, C, D соответственно, не лежащие на , образуют прямоугольник.
- Пусть M — середина дуги AB окружности . Пусть C и D лежат на и MC ∩ AB = E, MD ∩ AB = F. Докажите, что CDFE — вписанный.
- Дан вписанный четырёхугольник ABCD. Прямые AB и CD пересекаются в E, AD и BC — в F. Докажите, что точки пересечения биссектрис углов BEC и CFD со сторонами ABCD являются вершинами ромба.
- На сторонах BC и AD вписанного четырёхугольника ABCD отметили точки B’ и A’ соответственно, такие что BB’ = AA’ = AB. На продолжениях BC и AD за C и D отметили точки C’ и D’ соответственно, такие что CC’ = DD’ = CD. Докажите, что A’B’C’D’ — вписанный.
- (СПб МО, 2009, 11.3) В окружность вписан четырёхугольник ABCD. Касательный к , проведённые в точках A и D, пересекаются в точке P, при этом дуга ABCD лежит вне треугольника ADP. На луче BA нашлась такая точка K, что PK||AC, а на луче DC — точка N, такая, что PN||BD. Докажите, что точки B, C, K, N лежат на одной окружности.
- Пусть A 1 , B 1 , C 1 — основания соответствующих биссектрис в треугольнике ABC. Описанная окружность A 1 B 1 C 1 пересекает AB, BC, CA в C 2 , A 2 и B 2 соответственно. Докажите, что 2*max(A 1 A 2 , B 1 B 2 , C 1 C 2 ) = A 1 A 2 + B 1 B 2 + C 1 C 2 .
- Пусть B’ и C’ — основания перпендикуляров из B и C на внешнюю биссектрису угла A треугольника ABC. Докажите, что основание высоты треугольника, опущенной из A, середина стороны BC, B’ и C’ лежат на одной окружности.
- AA 1 — биссектриса треугольника ABC. O — центр описанной окружности ABC, O 1 — BAA 1 , O 2 — CAA 1 . Докажите, что OO 1 = OO 2 .
- (Окружность Ламуна) Медианы AD, BE и CF треугольника ABC пересекаются в точке M. Докажите, что центры описанных окружностей треугольников AME, AMF, BMD, BMF, CMD и CME лежат на одной окружности.
- ABCD — параллелограмм, O — его центр. Докажите, что O и проекции D на AB, BC и AC лежат на одной окружности.
- (Автор) K, L, M, N — проекции точки пересечения диагоналей вписанного четырёхугольника ABCD на AB, BC, CD и DA соответственно. H — пересечение перпендикуляров из середин AC и BD на BD и AC. Докажите, что середина KM, середина LN и H лежат на одной прямой.
- (X олимпиада имени И. Ф. Шарыгина, финал, 9 класс, задача 2, автор — Ф. Нилов) В четырехугольнике ABCD углы A и C — прямые. На сторонах AB и CD как на диаметрах построены окружности, пересекающиеся в точках X и Y. Докажите, что прямая XY проходит через середину диагонали AC.
- (Автор) Диагонали вписанного в окружность Г четырёхугольника ABCD пересекаются в точке P, прямые AB и CD — в E. Описанные окружности треугольников BCP и ADP с центрами в I и J пересекаются вторично в точке K. Описанная окружность IJK пересекают Г в точках X и Y. Докажите, что середина отрезка, соединяющего основания перпендикуляров из E на BC и AD лежит на XY.
- Внутри треугольника ABC выбрана произвольная точка P, A’, B’, C’ — проекции P на BC, AC и AB соответственно. Описанная окружность A’B’C’ вторично пересекает BC в X, прямая B’C’ пересекает прямую BC в Y. Докажите, что AX PY.
- (Автор) Диагонали вписанного четырёхугольника ABCD пересекаются в точке P, прямые AB и DC — в E, AD и BC — в F. Описанные окружности треугольников ACE и BDE вторично пересекаются в X; ACF и BDF — в Y; BCE и CDF — в Z. Докажите, что ZP — биссектриса угла XZY.
- (Автор) Диагонали вписанного четырёхугольника ABCD пересекаются в точке P. Описанные окружности треугольников ABP и CDP с центрами O 1 и O 2 вторично пересекаются в K 1 ; BCP и ADP с центрами в O 3 и O 4 — в K 2 ; Описанные окружности O 1 O 2 K 1 и O 3 O 4 K 2 пересекаются в X и Y. Докажите, что середина отрезка, соединяющего середины AC и BD лежит на XY.
- Хорды AC и BD окружности с центром O пересекаются в точке P. Докажите, что O ABO O CDO и O BCO O ADO пересекаются на OP.
- Хорды AC и BD окружности пересекаются в точке P. Проходящая через P прямая пересекает описанные окружности ABP и CDP и в точках K, L, M, N (K — L — M — N). Докажите, что KL = MN.
- Четыре окружности касаются внешним образом (каждая ровно с двумя другими) в точках A, B, C и D. Докажите, что ABCD вписанный.
- Диагонали вписанного четырёхугольника ABCD пересекаются в точке P, прямые AB и CD — в E. Описанная окружность EPD вторично пересекает описанную окружность ABCD в точке X. Докажите, что прямая AX проходит через середину отрезка EP.
Литература:
- Lozanovski, S. A Beautiful Journey Through Olympiad Geometry / S. Lozanovski. — version. 1.4. — 231 c. — Текст: непосредственный.
- Протасов, В. Ю. О двух велосипедистах и вишневой косточке / В. Ю. Протасов. — Текст: непосредственный // Квант. — 2008. — № 3. — С. 41–44.
- Жижилкин, И. Д. Инверсия / И. Д. Жижилкин. — Москва: МЦНМО, 2019. — 72 c. — Текст: непосредственный.
- Олимпиадная геометрия. — Текст: электронный // Дзен: [сайт]. — URL: https://dzen.ru/id/5d921a06a660d700ae014dfd.
- Ефремов, Д. Д. Новая геометрия треугольника / Д. Д. Ефремов. — Одесса: Матезис, 1902. — 334 c. — Текст: непосредственный.
- Прасолов, В. В. Задачи по планиметрии / В. В. Прасолов. — 8-е изд., испр. — Москва: МЦНМО, 2022. — 640 c. — Текст: непосредственный.
- Куликова, А. Теорема об изогоналях / А. Куликова, Д. Прокопенко. — Текст: непосредственный // Квант. — 2018. — № 4. — С. 41–44.
- Акопян, А. В. Геометрия в картинках / А. В. Акопян. — 1-е изд. — Москва: МЦНМО, 2011. — 130 c. — Текст: непосредственный.










