Свойства вписанного четырёхугольника. Часть 2



Полярное соответствие

— Полярой точки A относительно окружности  с центром в O и радиусом R называется прямая a такая, что a  OA и OA * OA’ = R ² , где A’ — основание перпендикуляра, опущенного из O на a.

— Полюсом прямой a относительно окружности  с центром в O и радиусом R называется точка A такая, что a  OA и OA * OA’ = R ² , где A’ — основание перпендикуляра, опущенного из O на a.

— Основное свойство полярного соответствия: если поляра точки A проходит через точку B, то поляра точки B так же проходит через точку A (док-во элементарно)

— Если точка A находится вне окружности  или на ней, то её поляра относительно  совпадает с прямой, проходящей через точки касания  и касательных к ней из точки A (док-во элементарно)

— Полярным преобразованием относительно окружности  называется преобразование, каждой прямой сопоставляющее её полюс относительно , а каждой точке — её поляру

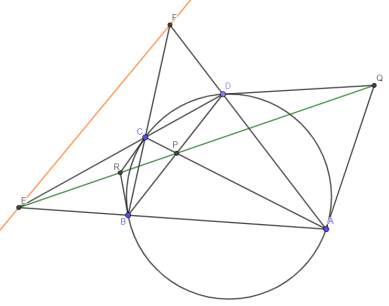
— Теорема Брокара: для вписанного ABCD P — полюс EF

Доказательство:

1) Пусть R — пересечение касательных к  в

B и C, а Q — в A и D, тогда, по теореме Паскаля (её док-во см., например, [1]) для AACDDB и для CCABBD имеем

Q — P — E и E — R — P, откуда R — P — Q

2) Т. к. F лежит на полярах R и Q, то RQ есть поляра F  P лежит на поляре F  F лежит на поляре P. Аналогично и E лежит на поляре P  EF есть поляра P  P — полюс EF, ч.т.д.

3*) Кроме того, E — полюс PF и F — полюс EF, а также из определения поляр следует, что O — ортоцентр PEF

Теорема о бабочке

— AB — хорда окружности  с центром в точке O. На прямой AB выбрана точка P. Перпендикуляр к OP в точке P пересекает касательные к  в A и B в X и Y. Докажите PX = PY

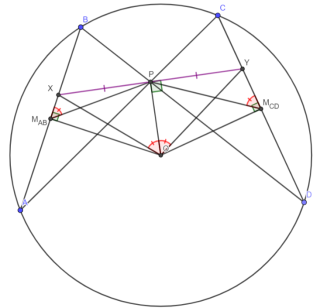
— (Теорема о бабочке) Диагонали вписанного четырёхугольника ABCD пересекаются в точке P, O — центр описанной окружности, докажите, что стороны AB и CD высекают равные отрезки на прямой, перпендикулярной OP и проходящей через P

Доказательство:

1) Пусть X и Y — точки пересечения перпендикуляра к OP в P и сторон AB и CD. Тогда, в силу OM _AB X = OXP = , XPOM _AB — вписанный, аналогично YPOM _CD  XOP = XM _AB P и YOP = YM _CD P

2) Поскольку PM _AB и PM _CD — соответственные элементы подобных треугольников ABP и CDP, то XM _AB P = YM _CD P  XOP = YOP  в треугольнике XOY высота OP является биссектрисой, а значит PX = PY, ч.т.д.

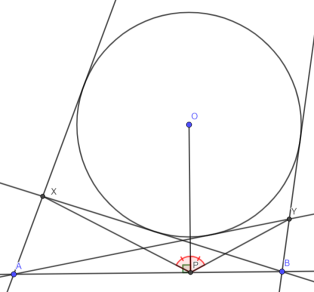
— (Двойственная теорема о бабочке) Из точек A и B проведены касательные к окружности с центром в точке O, пересекающиеся в точках X и Y (на каждой касательной по точке). P — основание перпендикуляра из O на прямую AB. Докажите, что XPO = YPO.

Указание к доказательству: сделайте полярное преобразование относительно , тогда X из теоремы о бабочке перейдет в XP, а Y — в YP. Задача сведется к равенству расстояний от O до XP и YP, что следует из теоремы о бабочке

Теорема Птолемея, её обобщения и еще несколько формул

— Теорема Птолемея: AC * BD = AB * CD + AD * BC (Для доказательства удобно отметить на AC точку X такую, что ABX = DBC и воспользоваться подобием)

— Вторая теорема Птолемея: (Для доказательства удобно представить S _ABCD как S _ABC + S _ADC и как S _BAD + S _BCD , а для площади треугольников воспользоваться формулой S = abc/4R)

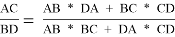
— Теорема Бретшнайдера: для произвольного четырёхугольника ABCD верно

(AC * BD) ² = (AB * DC) ² + (AD * BC) ^2– 2 * AB * BC * CD * DA *

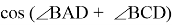
Указание к доказательству: на DA и AB построить PDA и ABQ, подобные ABC и ACD так, чтобы PD оказался || BQ и воспользоваться теоремой косинусов для PAQ

К слову, площадь произвольно четырёхугольника со сторонами a, b, c, d, полупериметром p и противоположными углами  и  вычисляется по формуле

, откуда, для вписанного

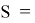
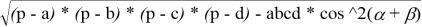
четырёхугольника:

(формула Брахмагупты), радиус же его описанной окружности можно вычислить по формуле

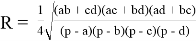
— Теорема Кэзи: для четырёх окружностей, касающихся пятой и имеющих длины касательных (в зависимости от “одноимённости” касания внутренних или внешних) t ₁₂ , t ₁₃ , t ₁₄ , t ₂₃ , t ₂₄ , t ₃₄ верно:

t ₁₃ * t ₂₄ = t ₁₂ * t ₃₄  t ₁₄ * t ₂₃ (Док-во см, например, [5])

Подробнее про теорему Птолемея можно почитать здесь: [4]

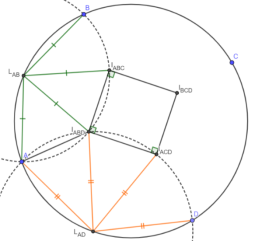
Ортодиагональный вписанный четырёхугольник и некоторые свойства замечательных точек

— Теорема Брахмагупты: если AC  BD, то M _BC P  AD

— Свойство 1.1: если AC  BD, то (O, CD) =

— Свойство 1.2: если AC  BD, то проекции P на стороны ABCD и середины этих сторон лежат на одной окружности

Доказательство: постольку P и O изогонально сопряжены (простой счет углов даёт изогональность), то их проекции на стороны лежат на одной окружности, ч.т.д.

— Свойство 1: H _ABD H _ACD CB — параллелограмм

Доказательство: поскольку каждый из отрезков BH _ABD и CH _ACD равен 2 * (O, AD) (известное свойство треугольника) и они параллельны, то H _ABD H _ACD CB — параллелограмм, ч.т.д.

— Свойство 2: AI _ABD I _ACD D — вписанный

Доказательство: по лемме о трезубце для ABD и для ACD LA = LI _ABD = LD и LA = LI _ACD = LD, где L — середина дуги AD  AI _ABD I _ACD D — вписанный, ч.т.д.

— Японская теорема: I _ABD I _ACD I _BCD I _ABC — прямоугольник

Доказательство: используя свойство 2 получаем: I _ABC I _ABD I _ACD = 2 — AI _ABD I _{ACD —} AI _ABD I _ABC = ABI _ABC + ADI _ACD = , аналогично и другие углы, ч.т.д. (Причем можно простым счётом углов проверить, что стороны этого прямоугольника будут параллельны биссектрисам угла между диагоналями)

— Свойство 3: P, O и точка пересечения перпендикуляров к BC и AD, восстановленных в C и D соответственно, лежат на одной прямой.

Доказательство:

1) Пусть Q и T — точки пересечения перпендикуляров к BC и AD, восстановленных в C и D и в B и A соответственно, а K и L — проекции P на BC и AD, тогда, очевидно, Q, O и T коллинеарны и достаточно проверить равенство

, которое очевидно следует из подобия APD и BPC

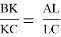
(От противного легко проверить, что если на некоторых прямых отметить точки A, B, C и A’, B’, C’ так, что , то 3 точки пересечения пер-ов, восстановленных к прямым в исходных точках будут лежать на одной прямой)

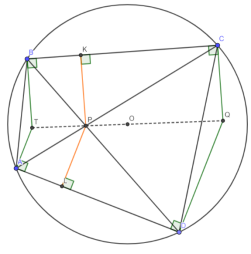
“Школьные” методы доказательства некоторых теорем

— Пусть (ABP) ∩ (CDP) = M ₁ , (BCP) ∩ (ADP) = M ₂ , тогда

1) M ₁ и M ₂ будут точками Микеля ломаных ACDB и ACBD. Отсюда моментально получаем вписанность ECM ₁ A, EDM ₁ B, FCM ₂ A, FDM ₂ B

2) E — P — M ₁ и F — P — M ₂ как радикальные оси зелёных и пунктирных окружностей (см. чертёж)

3) AOB = ADP + BCP = AM ₂ B (из пунктирных окружностей)  AOM ₂ B — вписанный, аналогично DOM ₂ C, BOM ₁ C и AOM ₁ D тоже вписанные, тогда, опять же как радикальные оси описанных окружностей этих четырехугольников, E — M ₂ — O, F — M ₁ — O, кроме того,

EM ₂ * EO = EB * EA = EP * EM ₁ , откуда OPM ₁ M ₂ — вписанный

4) OM ₂ * OE = OE ² — EM ₂ * OE = OE ² — (OE ² — R ² ) (квадрат касательной) = R ² , аналогично OM ₁ * OF = R ²  EM ₂ M ₁ F — вписанный, но, в силу вписанности и OPM ₁ M ₂ , OM ₂ P = OM ₁ P = (равны и в сумме составляют )  P — ортоцентр OEF, о чём, по сути, и говорит теорема Брокара

5) Кроме того, FM * FE = FP * FM ₂ = FC * FB  CEMB — вписанный, аналогично DFMC вписанный 

M — точка Микеля ABCD  O — P — M

6) Легко проверить, что AMO = AMC, тогда, т. к. OA = OC, AOCM будет вписанным по признаку. Аналогично и BODM

Задачи

1. (Из материалов IMO, 1996) O и H — центр описанной окружности и точка пересечения высот треугольника ABC соответственно. A’ — основание высоты из A на BC. Точка B’ на AC такова, что B’A’O = . Докажите, что A’HB’ = BCA.

Решение:

1) Пусть AA’ ∩ описанную окружность в точке D, а A’B’ BD — в E

2) Широко известно, что HA’ = A’D, кроме того, по теореме о бабочке B’A’ = A’E; HA’B’ и EA’D — вертикальные  A’ED = HA’B’

3) BCA = A’DE = A’HB’, ч.т.д.

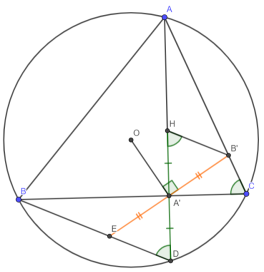
2. (Теорема Фейербаха). Окружность девяти точек треугольника касается его вписанной и вневписанных окружностей.

Доказательство:

1) Пусть A’, B’ и C’ — середины BC, AC и AB соответственно, а A ₁ , B ₁ и C ₁ — точки касания вписанной окружности со сторонами; BC = a, AC = b, AB = c, p =

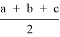
2) Если рассматривать A’, B’ и C’ как окружности нулевого радиуса, то нам достаточно проверить условие обратной теоремы Кэзи: A’C’ * B’B ₁ = A’A ₁ * B’C’ + C’C ₁ * A’B’, т. е. , что очевидно. Их точка касания называется точкой Фейербаха треугольника

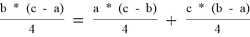
3) Аналогично и с вневписанными окружностями

3. (Л. А. Емельянов) Пусть ABC — произвольный треугольник, а M — точка внутри треугольника. Проведём через точку M три чевианы, основания которых — A ₁ , B ₁ , C ₁ . Построим вне треугольника три окружности, касающиеся сторон треугольника в основаниях чевиан и описанной окружности, и четвёртую, касающуюся этих трёх внешним образом. Тогда эта окружность касается вписанной окружности треугольника внутренним образом.

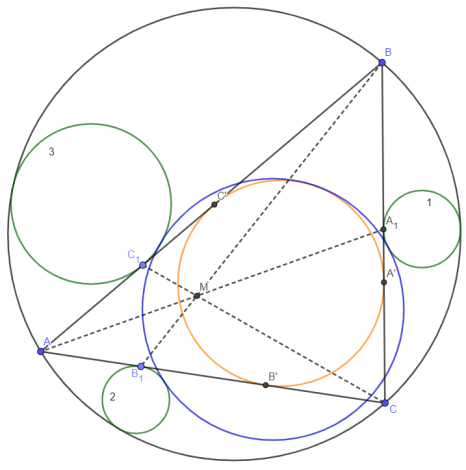
1) Обозначим для удобства AB = c, AC = b, BC = a, p = , AC ₁ = x, C ₁ B = x’, BA ₁ = y, A ₁ C = y’, CB ₁ = z, B ₁ A = z’. A’, B’, C’ — точки касания вписанной окружности со сторонами BC, AC и AB соответственно. “Маленькую” окружность, касающуюся BC, обозначим за 1, AC — за 2, AB — за 3, вписанную — за . t _{1 A —} длина касательной из A к 1, аналогично и остальные (для двух окружностей — длина внутренней касательной).

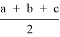
2) Применим теорему Кэзи для A, B, 1, C: t _{1 A} t _BC = t _AB t _{1 C} + t _AC t _{1 B} , откуда t _{1 A} = , аналогично t _{2 B} = , t _{3 C} =

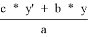
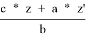
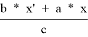
3) Применим теорему Кэзи для B, C, 2, 3: t _{3 C} t _{2 B} = t _CB t ₂₃ + t _{2 C} t _{3 B} , откуда, подставляя результаты п.2: t ₂₃ = , аналогично t ₁₃ = , t ₁₂ =

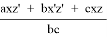
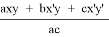
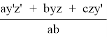
4) t _{1 } = (p — c) — y’, t _{2 } = z’ — (p — a), t _{1 } = x’ — (p — b). Подставим полученные выражения в условие обратной теоремы Кэзи для 1, 2, 3 и :

t ₁₂ t _{3 } — t ₁₃ t _{2 } — t ₂₃ t _{1 } = , что, в силу равенства xyz = x’y’z’, следующего из теоремы Чевы, равно 0  t ₁₂ t _{3 } = t ₁₃ t _{2 } + t ₂₃ t _{1 }  окружность, касающаяся 1, 2 и 3 внешним образом также касается  внутренним образом, ч.т.д.

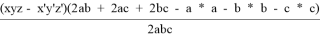
4. (Romanian Masters, 2013, задача 3, автор — М. А. Кунгожин) Четырёхугольник ABCD вписан в окружность . Прямые AB и CD пересекаются в точке P, AD и BC — в Q, диагонали AC и BD — в R. Пусть M — середина PQ. Точка K — общая точка прямой MR и . Докажите, что описанная окружность KPQ касается .

Решение:

1) Пусть O — центр , Y — проекция O на MR, OY ∩ PQ = U.

2) По теореме Брокара PQ — поляра R  по основному св-ву полярного соответствия R лежит на поляре U. Но MR  OU  MR — поляра U  UK — касательная к   UK ² = UY * UO (из пр/у треугольника OKU)

3) По теореме Брокара R — ортоцентр OPQ  X, симметричная R относительно M,  (OPQ) (PXQ = PKQ = POQ), причем XPRQ — п-мм  OPX = OYX = (QR  OP  XP  OP)  Y  (OPQ)  UQ * UP = UY * UO = (п.1) UK ²  (PKQ) касается , ч.т.д.

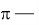
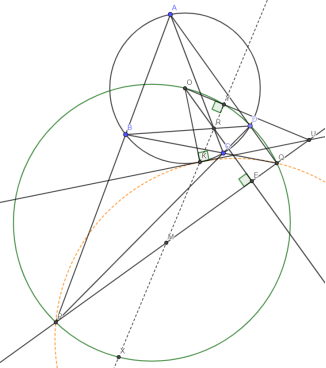
Задачи для самостоятельного решения

1. Дан вписанный шестиугольник A ₁ A ₂ A ₃ A ₄ A ₅ A ₆ . Докажите, что A ₁ A ₄ *A ₂ A ₄ *A ₃ A ₆ = A ₁ A ₂ *A ₃ A ₆ *A ₄ A ₅ + A ₂ A ₃ *A ₁ A ₄ *A ₅ A ₆ + A ₃ A ₄ *A ₂ A ₅ *A ₆ A ₁ .
2. Высоты BB’ и CC’ треугольника ABC пересекаются в точка H. Прямая B’C’ пересекает прямую BC в точке E. M — середина BC. Докажите, что MH  AE.
3. H — точка пересечения высот ABC, M — середина BC. Перпендикуляр к MH в H пересекает прямые AB и AB в X и Y. Докажите, что HX = HY.
4. Вневписанная окружность треугольника ABC, касающаяся стороны BC, касается AB, CB и AC в C ₁ , A ₁ и B ₁ — соответственно. I — центр вписанной окружности ABC. IX и IY — касательные из I к вневписанной окружности, касающейся BC. Докажите, что середины отрезков C ₁ A ₁ и B ₁ A ₁ и точки X и Y лежат на одной прямой.
5. (Польская национальная олимпиада, финал, задача 5. Автор — Dominik Burek) Точка M — середина стороны BC треугольника ABC. Точка P на стороне AB такова, что AP > BP. Точка Q на стороне AC такова, что ∠BPM = ∠CQM. Серединные перпендикуляры к BC и PQ пересекаются в точке S. Докажите, что ∠BAC + ∠QSP = ∠QMP.
6. (ВСОШ, заключительный этап, 2009/2010, 11.3) Четырехугольник ABCD вписан в окружность ω, а его диагонали пересекаются в точке K. Точки M ₁ , M ₂ , M ₃ , M ₄ — середины дуг AB, BC, CD, DA (не содержащих других вершин четырехугольника) соответственно. Точки I ₁ , I ₂ , I ₃ , I ₄ — центры окружностей, вписанных в треугольники ABK, BCK, CDK, DAK соответственно. Докажите, что прямые M ₁ I ₁ , M ₂ I ₂ , M ₃ I ₃ , и M ₄ I ₄ пересекаются в одной точке.
7. Вписанная окружность треугольника ABC с центром I касается стороны AC в точке Q; точка E — середина стороны AC, а K — точка пересечения высот треугольника BIC. Докажите, что KQ  IE.
8. ABCD — описанный четырёхугольник. AB ∩ CD = E, AD ∩ BC = F, AC ∩ BD = P. X — основание перпендикуляра из P на EF. Докажите, что AXP = PXC.
9. (По мотивам Romanian Masters, 2013, задачи 3) Четырёхугольник ABCD вписан в окружность . Прямые AB и CD пересекаются в точке P, AD и BC — в Q, диагонали AC и BD — в R. Пусть M — середина PQ. Прямая MR пересекает  в точках K и L. Докажите, что PKQ + PLQ = .
10. (XVIII олимпиада имени И. Ф. Шарыгина, финал, 10 класс, задача 4, авторы — А. Матвеев, И. Фролов) Выпуклый четырехугольник ABCD таков, что ∠B = ∠D. Докажите, что середина диагонали BD лежит на общей внутренней касательной к окружностям, вписанным в треугольники ABC и ACD.